
All Solutions
Page 420: Closure Activity
$$
color{#4257b2}text{(a) First figure.}
$$
$because$ All of lengths are equals.
$therefore$ Two triangles are equals.
$$
color{#4257b2}text{(b) Second figure.}
$$
$because$ There are two lengths in triangles are equals.
$because$ There is one angle in triangles is equals.
$therefore$ Two triangles are equals.
$$
color{#4257b2}text{(c) Third figure.}
$$
$because$ There are two lengths in triangles are equals.
$because$ There is one angle in triangles is equals.
$therefore$ Two triangles are equals.
text{color{Brown}The triangles are equals.}
$$
We know that the equation form for the line is $y=a x+b$
$$
4=(acdot-5)+b -5a+b=4
$$
$$
-2=(acdot3)+b 3a+b=-2
$$
Use elimination property as follows:
$$
(-5a-3a)+(b-b)=4-(-2) -8a=6
$$
Divide both of sides by $-8$ as follows:
$$
a=dfrac{6}{-8} a=-dfrac{3}{4}
$$
Substitute the value of $a=-dfrac{3}{4}$ in the first equation as follows:
$$
-5left(-dfrac{3}{4}right)+b=4 dfrac{3cdot5}{4}+b=4
$$
$$
dfrac{15}{4}+b=4 b=4-dfrac{15}{4}
$$
$$
b=dfrac{16-15}{4} \ b=dfrac{1}{4}
$$
$$
color{#4257b2}y=a x+b y=-dfrac{3}{4} x+dfrac{1}{4}
$$
text{color{Brown}$y=-dfrac{3}{4} x+dfrac{1}{4}$}
$$
$$
dfrac{4}{10}=dfrac{5}{x+5}
$$
Isolate variables on left side as follows:
$$
4(x+5)=10cdot5 4x+20=50
$$
$$
4x=50-20 4x=30
$$
Divide both of sides by $4$ as follows:
$$
x=dfrac{30}{4} x=7.5
$$
text{color{Brown}$x=7.5$}
$$
$$
begin{align*}
y&=3x+2\
6x&-2y=8
end{align*}
$$
We can try to solve this system by using the Substitution method. Substitute the value of $y$ from the first equation $y=3x+2$ into the equation $6x-2y=8$ and try to solve for the value of $x$ in the resulting equation only in terms of $x$ as shown below.
$$
begin{align*}
6x-2y&=8\
6x-2(3x+2)&=8\
6x-6x-4&=8\
-4&=8tag{not true}
end{align*}
$$
While solving the above system, we got a non-true equality which shows that there are no possible solutions for this system. While substitution, the variables of the system gets canceled on both the side and we get a false equality.
$bullet$ For $y=3x+2$
Let $x=0$
$$
begin{align*}
y&=3x+2\
y&=3(0)+2\
y&=2
end{align*}
$$
Therefore, the point is $(0,2)$
Now, for another point on this line, Let $x=1$
$$
begin{align*}
y&=3x+2\
y&=3(1)+2\
y&=5
end{align*}
$$
Therefore, the 2 points on the line $y=3x+2$ are $(0,2)$ and $(1,5)$. We can locate these points on the graph and we can easily draw a stright line through them.
$bullet$ For $6x-2y=8$
Let $x=0$
$$
begin{align*}
6(0)-2y&=8\
y&=dfrac{8}{-2}\
y&=-4
end{align*}
$$
Therefore, the point is $(0,-4)$
Now, for another point on this line, Let $x=1$
$$
begin{align*}
6(1)-2y&=8\
-2y&=8-6\
y&=dfrac{2}{-2}\
y&=-1
end{align*}
$$
Therefore, the 2 points on the line $6x-2y=8$ are $(0,-4)$ and $(1,-1)$.We can locate these points on the graph and we can easily draw a straight line through them.
$textbf{(b)}$ From the graph of the system, we can see that the given lines are parallel to each other and therefore, they will not intersect each other anywhere. This situation well explains the no solution case with the equations.
Determine the solution of the equation.
$$
begin{align*}
18x – 3 left(6x – 3 right) & = 9 && {text {use substitution method}} \
18x – 18x + 9 & = 9 && {text {evaluate}} \
9 & = 9 && {text {infinite number of solution}}
end{align*}
$$
Since there is no definite value of the variable, any point on the line may be considered as solution to the equation.
Both equations form the same line having the same slope and same and same $y$-intercept which indicates an infinite number of solution.
Graph of the equation.
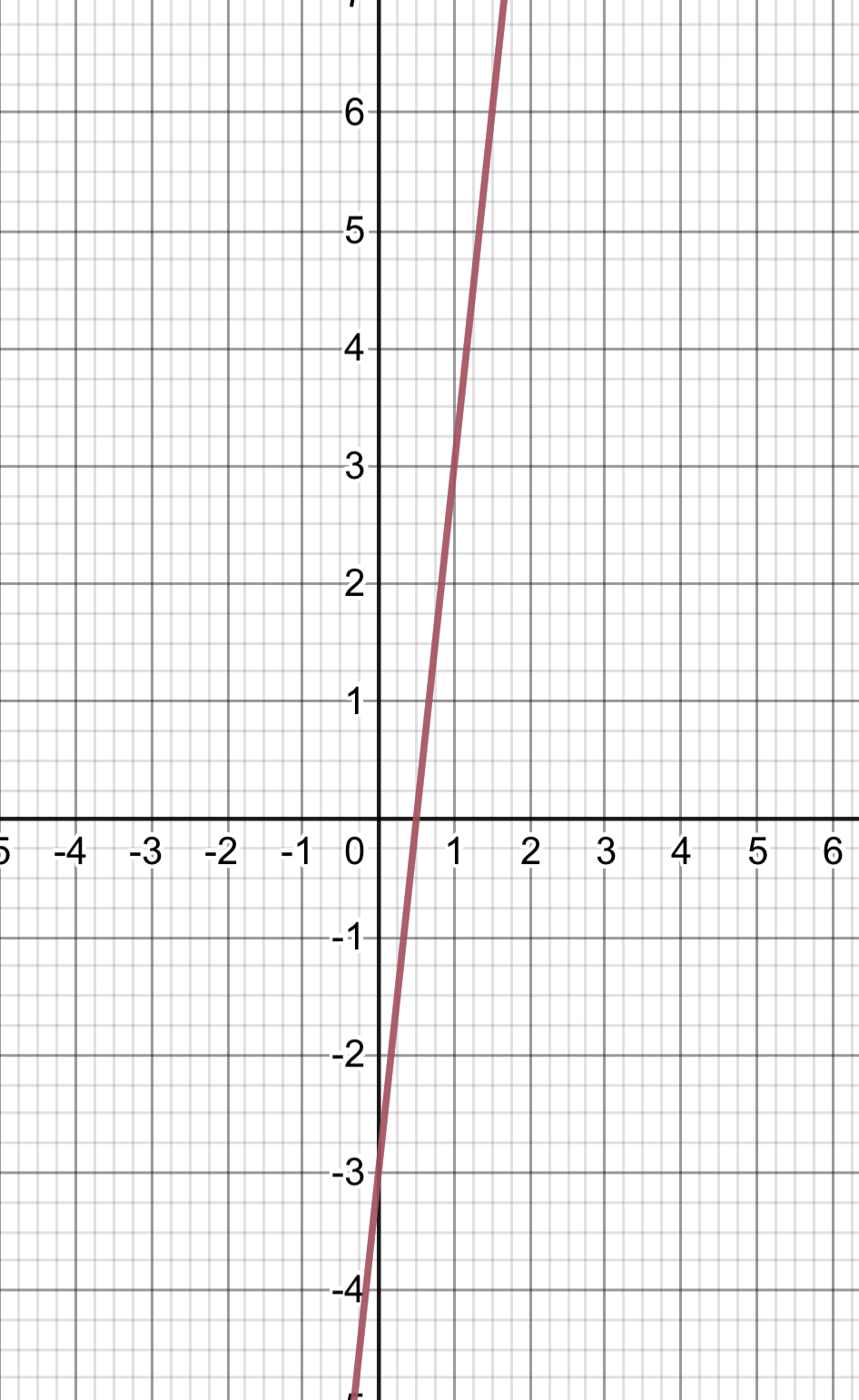
b. The system of equation forms the same line.
$$
color{#4257b2}text{(a)} x+2y=17 x-y=2
$$
Using elimination property for the new equations as follows:
$$
(x-x)+(2y-(-y))=(17-2) 3y=15
$$
Divide both of sides by $3$ as follows:
$$
y=dfrac{15}{3} y=5
$$
Substitution the value of $y=5$ for first equation as follows:
$$
x+(2cdot5)=17 x+10=17
$$
$$
x=17-10 x=7
$$
color{#4257b2}text{(b)} 4x+5y=11 2x+6y=16
$$
Multiply the second equ. by $2$ to get $4x+12y=32$
Using elimination property for the new equations as follows:
$$
(4x-4x)+(5y-12y)=(11-32) -7y=-21
$$
Divide both of sides by $-7$ as follows:
$$
y=dfrac{-21}{-7} y=3
$$
Substitution the value of $y=3$ for first equation as follows:
$$
4x+(5cdot3)=11 4x+15=11 4x=11-15
$$
$$
4x=-4 x=-dfrac{4}{4} x=-1
$$
color{#4257b2}text{(c)} 4x-3y=-10 x=dfrac{1}{4} y-1
$$
Substitution the value of $x$ for first equation as follows:
$$
4left(dfrac{1}{4}y-1right)-3y=-10 y-4-3y=-10
$$
$$
-2y=-10+4 -2y=-6
$$
Divide both of sides by $-2$ as follows:
$$
y=dfrac{-6}{-2} y=3
$$
Substitution the value of $y=3$ for first equation as follows:
$$
x=dfrac{1}{4}y-1 x=dfrac{1}{4}cdot3-1
$$
$$
x=dfrac{3}{4}-1 x=-dfrac{1}{4}
$$
color{#4257b2}text{(d)} 2x+y=-2x+5 3x+2y=2x+3y
$$
$$
2x+2x+y=5 4x+y=5
$$
$$
3x-2x+2y-3y=0 x-y=0
$$
Multiply the second equ. by $-1$ to get $-x+y=0$
Using elimination property for the new equations as follows:
$$
(4x-(-x))+(y-y)=(5-0) 4x+x=5 5x+5
$$
$$
x=dfrac{5}{5} x=1
$$
Substitution the value of $x=1$ for second equation as follows:
$$
x-y=0 1-y=0 y=1
$$
text{color{Brown}(a) $x=7 y=5$ (b) $x=-1 y=3$
\ \
(c) $x=-dfrac{1}{4} y=3$ (d) $x=1 y=1$}
$$
$(t)$ Mean the time and $(d)$ mean the distance.
Speed $=$ distance$div$time
Jaun speed $=55=dfrac{d}{t} d=55 t$
Patrolman speed $=70=dfrac{d+2}{t} d+2=70 t$
Substitution value of $d$ in second equation as follows:
$$
55t+2=70t 70t-55t=2 15t=2
$$
Divide both of sides by $15$ as follows:
$$
t=dfrac{2}{15} t=0.13333text{ hour}
$$
$$
t=0.13333cdot60 t=8text{ minute}
$$
text{color{Brown}$t=0.13333$ hours $t=8$ minute}
$$

