a.

In the given equation $y=3x+4$ , when $x=0$ which means time is zero seconds, value of y which shows distance is
4 meters. Therefore, Georgia got head start of 4 meters.

b.

For calculating the Rate of speed for the Georgia, we need to differentiate the given equation. As speed is given by $dfrac{Deltatext{ distance}}{Delta text{time}}$, where $Delta mathrm{t} rightarrow 0$ which in this case can be represented by $dfrac{Delta mathrm{y}}{Delta mathrm{ x}}$ where $Delta mathrm{x} rightarrow 0$ or simply by $dfrac{dy}{dx}$.

$$
begin{align*}
y&=3x+4\
Rightarrow dfrac{dy}{dx}&=3
end{align*}
$$

Therefore, speed of Georgia is 3 meters/seconds.

$a.$ 4 meters

$b.$ 3 meters/seconds

$textbf{(a)}$ The given equation of the line is $-6x+2y=10$.

The slope of the line given in this form can be calculated by finding any two pair of points on this line and then calculating the slope by the method shown below.

First we need to assume the value of any one coordinate let say $x$ and then put it into the given equation and solve for $y$ then the point $(x,y)$ will lie on the given line.

$bullet$ Let $x=0$

$$
begin{align*}
-6x+2y&=10\
-6(0)+2y&=10\
2y&=10tag{divide each side by 2}\
y&=5
end{align*}
$$

Therefore, $(0,5)$ is a point on the line $-6x+2y=10$

Similarly let $y=2$

$$
begin{align*}
-6x+2y&=10\
-6x+2(2)&=10\
-6x+4&=10tag{subtract 4 from each side}\
-6x&=6tag{divide each side by -6}\
x&=-1
end{align*}
$$

Therefore, $(-1,2)$ is a point on the line $-6x+2y=10$

Now, that we have two pair of points on this line. Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

Now, we have given points as $(0,5)$ and $(-1,2)$. Let $(x_1,y_1)=(0,5)$ and $(x_2,y_2)=(-1,2)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{2-5}{-1-0}\
&=dfrac{-3}{-1}\
&=3
end{align*}
$$

Therefore, the slope of the given line is 3.

$bullet$The $y-$ intercept of a line is the value of output variable $y$ where the input variable $x=0$ therefore, as we calculated above, for $x=0$ we got $y=5$ hence, the $y-$ intercept of a line is 5.

textbf{(b)} We can find the points on the given line by the method explained in the part (a). The table of points on the line is attached below.\
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
-2&-1\
hline
-1.67&0\
hline
-1&2\
hline
0&5\
hline
1&8\
hline
end{tabular}
end{center}
The graph of the can be drawn through these point by locating these points on the graph paper.\ The equivalent form of the given line is $y=3x+5$\

$textbf{(c)}$ We can rearrange the given equation by using the steps shown below.

$$
begin{align*}
-6x+2y&=10tag{add $6x$ to the each side}\
-6x+6x+2y&=6x+10\
2y&=6x+10tag{divide each term by 2}\
dfrac{2y}{2}&=dfrac{6x}{2}+dfrac{10}{2}\
y&=3x+5
end{align*}
$$

Yes, this new equation matches with the part (b).

$textbf{(a)}$ The slope of the line is 3 and $y$-intercept is 5.

$textbf{(b)}$ The table and graph is attached inside. The equivalent form is $y=3x+5$

$textbf{(c)}$ Yes, the new equation matches with the part (b).

The general form any equation of a line is given by
$$
y=mx+c
$$
where $m$ represents the slope and $c$ represents the $y$-intercept. So for each part, we will rearrange the given equation in this form so that we can easily find the slope and $y$-intercept by comparing is with general form.

$textbf{(a)}$
$$
begin{align*}
2x+y&=3x-7tag{subtract $2x$ from each side}\
2x-2x+y&=3x-2x-7\
&boxed{y=x-7}
end{align*}
$$

The slope of the given line is equal to 1 and the $y$-intercept is equal to $-7$

Now, for finding any point on the given line, first, we assume the value of any one coordinate and then put it into the equation and solve for the other.
$bullet$ Let $x=1$

$$
begin{align*}
2x+y&=3x-7\
2(1)+y&=3(1)-7\
2+y&=-4\
y&=-6
end{align*}
$$

Therefore, we got $(1,-6)$ is a point on the given line. Now we verify if this satisfies our algebraically rearranged equation or not.

$$
begin{align*}
y&=x-7\
(-6)&=(1)-7\
-6&=-6tag{true always}
end{align*}
$$

We can see that point $(1,-6)$ satisfies both the equations. Yes, it makes both the equation true.

$textbf{(b)}$
$$
begin{align*}
x+2y&=3x+4tag{subtract $x$ from each side}\
x-x+2y&=3x-x+4\
2y&=2x+4tag{divide each side by 2}\
&boxed{y=x+2}
end{align*}
$$

The slope of the given line is equal to 1 and the $y$-intercept is equal to $2$

Now, for finding any point on the given line, first, we assume the value of any one coordinate and then put it into the equation and solve for the other.
$bullet$ Let $x=1$

$$
begin{align*}
x+2y&=3x+4\
(1)+2y&=3(1)+4\
1+2y&=7\
2y&=6\
y&=3
end{align*}
$$

Therefore, we got $(1,3)$ is a point on the given line. Now we verify if this satisfies our algebraically rearranged equation or not.

$$
begin{align*}
y&=x+2\
(3)&=(1)+2\
3&=3tag{true always}
end{align*}
$$

We can see that point $(1,3)$ satisfies both the equations. Yes, it makes both the equation true.

$textbf{(c)}$
$$
begin{align*}
3y+2&=2y-5xtag{subtract $2y+2$ from each side}\
3y-2y-2+2&=2y-2y-2-5x\
&boxed{y=-5x-2}
end{align*}
$$

The slope of the given line is equal to 1 and the $y$-intercept is equal to $2$

$bullet$ Let $y=1$

$$
begin{align*}
3y+2&=2y-5x\
3(1)+2&=2(1)-5x\
5&=2-5x\
3&=-5x\
x&=-dfrac{3}{5}
end{align*}
$$

Let’s verify if $(-dfrac{3}{5},1)$ satisfies our algebraically rearranged equation or not.

$$
begin{align*}
y&=-5x-2\
(1)&=-5(-dfrac{3}{5})-2\
(1)&=(3)-2\
1&=1tag{true always}
end{align*}
$$

We can see that point $(-dfrac{3}{5},1)$ satisfies both the equations. Yes, it makes both the equation true.

$textbf{(d)}$
$$
begin{align*}
2(y-3)&=2x-6tag{use distributive property}\
2y-6&=2x-6tag{add 6 to the each side}\
2y&=2xtag{divide each side by 2}\
&boxed{y=x}
end{align*}
$$

The slope of the given line is equal to 1 and the $y$-intercept is equal to $0$

$bullet$ Let $y=1$

$$
begin{align*}
2(y-3)&=2x-6\
2((1)-3)&=2x-6\
-4&=2x-6\
-4+6&=2x\
2&=2x\
x&=1
end{align*}
$$

Let’s verify if $(1,1)$ satisfies our algebraically rearranged equation or not.

$$
begin{align*}
y&=x\
(1)&=(1)\
1&=1tag{true always}
end{align*}
$$

We can see that point $(1,1)$ satisfies both the equations. Yes, it makes both the equation true.

$textbf{(e)}$
$$
begin{align*}
5-3(x+1)&=2y-3x+2tag{use distributive property}\
5-3x-3&=2y-3x+2\
-3x+2&=2y-3x+2tag{add $3x-2$ to the each side}\
-3x+3x-2+2&=2y-3x+3x-2+2\
0&=2y\
&boxed{y=0}
end{align*}
$$

The slope of the given line is equal to 0 and the $y$-intercept is equal to $0$

We will get any $y=0$ for any value of $x$ and this is because in the given equation the term of variable $x$ gets cancelled. Therefore, both the lines are same.

$textbf{(f)}$
$$
begin{align*}
x-(y+2)&=2(2x+1)tag{use distributive property}\
x-y-2&=4x+2tag{add $2-x$ to the each side}\
x-y-2 +(2-x)&=4x+2+(2-x)\
-y&=3x+4tag{multiply each side by -1}\
y&=-3x-4\
&boxed{y=-3x-4}
end{align*}
$$

The slope of the given line is equal to -3 and the $y$-intercept is equal to $-4$

$bullet$ Let $x=1$ for the equation $y=-3x-4$

$$
begin{align*}
y=-3(1)-4\
y&=-7
end{align*}
$$

Let’s verify if $(1,-7)$ satisfies our original equation or not.

$$
begin{align*}
x-(y+2)&=2(2x+1)\
1-(-7+2)&=2(2(1)+1)\
1-(-5)&=2(3)\
6&=6tag{true always}
end{align*}
$$

Yes, it makes both the equation true.

$textbf{(a)}$ $y=x-7$

$textbf{(b)}$ $y=x+2$

$textbf{(c)}$ $y=-5x-2$

$textbf{(d)}$ $y=x$

$textbf{(e)}$ $y=0$

$textbf{(f)}$ $y=-3x-4$

$textbf{(a)}$ The equation $0=3x-5$ have only one variable. This equation have a single solution $x=dfrac{5}{3}$. We cannot represent this point on the graph unless we assume that the given equation is of two variables $x$ and $y$ and variable $y$ is hidden. For this case, it will represent the line $x=dfrac{5}{3}$ and have infinitely many solutions. The line is shown on the graph attached below.

$textbf{(b)}$ The equation $y=3x-5$ has two variables which are $x$ and $y$. This represents a line which can have infinitely many solutions. We can show the solutions graphically by using the line, graph of which is attached below and some of the solution points are shown in purple colour

$textbf{(c)}$ The given function $y=0.2x^3-5$ has infinitely many solutions. If we assume $x$ as the input variable and $y$ as the output variable, we can see that corresponding to each value of $x$ we get a unique value of $y$. Therefore, we can say that the equation has many solutions, some of which are shown on the graph attached below.

$textbf{(d)}$ No, $(5,8)$ cannot be the solution of the given function. From the graph we can see that it is an increasing function and it attains output value $8$ at an input close to 4. So on the input value of $5$ the function output value will be much greater than 8 which in fact is $20$.

$textbf{(e)}$ We can estimate the solution by observing the graph and approximating the value of $x$ for which the given function attains $4$. From the graph see that function attains output value of 4 for the input which lies between 2 and 3.

$textbf{(a)}$ Single variable, single solution, cannot be located on the graph.

$textbf{(b)}$ two variables, Infinitely many solutions, can be represented by a line on the graph.

$textbf{(c)}$ Infinitely many solutions.

$textbf{(d)}$ No

$textbf{(e)}$ Input variable will lie between 2 and 3 for the output of 4.

$textbf{(a)}$ We can rearrange the given equation $W=Fd$ to obtain the $F$ as output variable by dividing the both side by the distance $(d)$.

$$
begin{align*}
W&=Fdtag{divide each side by $d$}\
dfrac{W}{d}&=dfrac{Fd}{d}\
dfrac{W}{d}&=Ftag{interchange sides}\
&boxed{F=dfrac{W}{d}}
end{align*}
$$

$textbf{(b)}$
$$
begin{align*}
F&=dfrac{9C}{5}+32tag{subtract 32 from the each side}\
F-32&=dfrac{9C}{5}+32-32\
F-32&=dfrac{9C}{5}tag{Multiply each side by $dfrac{5}{9}$}\
(F-32)cdot dfrac{5}{9}&=dfrac{9C}{5}cdot dfrac{5}{9}\
(F-32)cdot dfrac{5}{9}&=Ctag{interchange sides}\
C&=(F-32)cdot dfrac{5}{9}tag{use distributive property}\
C&=dfrac{5F}{9}-32cdot dfrac{5}{9}\
&boxed{C=dfrac{5F}{9}-dfrac{160}{9}}
end{align*}
$$

$textbf{(d)}$
$$
begin{align*}
rho&=dfrac{m}{v} tag{multiply each side by $v$}\
rho cdot v&=dfrac{m}{v} cdot v\
rho v&=m tag{interchange sides}\
&boxed{m=rho v}
end{align*}
$$

$textbf{(a)}$ $F=dfrac{W}{d}$

$textbf{(b)}$ $C=dfrac{5F}{9}-dfrac{160}{9}$

$textbf{(c)}$ $m=rho v$

$textbf{(a)}$
$$
begin{align*}
y^0+y^1&=dfrac{1}{x^{-2}}tag{use $a^0=1$ and $a^{1}=a$}\
1+y&=dfrac{1}{x^{-2}} tag{use $dfrac{1}{a^{-m}}=a^m$ }\
1+y&=x^2 tag{subtract 1 from each side}\
1-1+y&=x^2-1\
&boxed{y=x^2-1}
end{align*}
$$

$textbf{(b)}$
$$
begin{align*}
d&=(r+c)ttag{divide each side by $t$}\
dfrac{d}{t}&=dfrac{(r+c)t}{t}\
dfrac{d}{t}&=r+ctag{subtract $c$ from each side}\
dfrac{d}{t}-c&=r+c-c\
dfrac{d}{t}-c&=rtag{interchange sides}\
&boxed{r=dfrac{d}{t}-c}
end{align*}
$$

$textbf{(c)}$
$$
begin{align*}
x^2+4y&=(x+6)(x-2)tag{use distributive property}\
x^2+4y&=x(x-2)+6(x-2)\
x^2+4y&=x^2-2x+6x-12tag{subtract $x^2$ from each side}\
x^2-x^2 +4y&=x^2-x^2+4x-12\
4y&=4x-12tag{divide each side by 4}\
dfrac{4y}{4}&=dfrac{4x-12}{4}\
&boxed{y=x-3}
end{align*}
$$

$textbf{(d)}$
$$
begin{align*}
3(2x+4)&=2+6x+10tag{use distributive property}\
6x+12&=6x+12tag{subtract $6x$ from the each side}\
12&=12tag{true always}
end{align*}
$$

The term of the variable $x$ gets cancelled out on each side, but the equation is true which means that $xrightarrow (-infty,+ infty)$

$textbf{(a)}$ $y=x^2-1$

$textbf{(b)}$ $r=dfrac{d}{t}-c$

$textbf{(c)}$ $y=x-3$

$textbf{(d)}$ The term of the variable $x$ gets cancelled out on each side, but the equation is true which means that $xrightarrow (-infty,+ infty)$

$textbf{(a)}$
$$
begin{align*}
3x-2y&=18tag{add $2y$ to the each side}\
3x-2y+2y&=18+2y\
3x&=18+2ytag{divide each side by 3}\
dfrac{3x}{3}&=dfrac{18+2y}{3}\
x&=dfrac{18}{3}+dfrac{2y}{3}\
&boxed{x=dfrac{2y}{3}+6}
end{align*}
$$

$textbf{(b)}$
$$
begin{align*}
3x-2y&=18tag{subtract $3x$ from the each side}\
3x-3x-2y&=18-3x\
-2y&=18-3xtag{divide each side by $-2$}\
dfrac{-2y}{-2}&=dfrac{18-3x}{-2}\
y&=dfrac{18}{-2}+dfrac{-3x}{-2}\
&boxed{y=dfrac{3x}{2}-9}
end{align*}
$$

$textbf{(c)}$
$$
begin{align*}
C&=2pi r tag{divide each side by $2pi$}\
dfrac{C}{2pi}&=dfrac{2pi r}{2pi}\
dfrac{C}{2pi}&=rtag{interchange sides}\
&boxed{r=dfrac{C}{2pi}}
end{align*}
$$

$textbf{(a)}$ $x=dfrac{2y}{3}+6$

$textbf{(b)}$ $y=dfrac{3x}{2}-9$

$textbf{(c)}$ $r=dfrac{C}{2pi}$

$textbf{(a)}$ $bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=78x-126
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(6)cdot(13x-21)\
&=6(13x)+6(-21)\
&=78x-126
end{align*}
$$

We can see that Areas from both the cases is the same hence, so we can write it as shown below.

$$
text{Area}=6 cdot(13x-21)=78x-126
$$

$textbf{(b)}$ $bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=x^2+3x-5x-15\
&=x^2-2x-15
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(x-5)cdot(x+3)\
&=x(x+3)+-5(x+3)\
&=(x^2+3x) + (-5x-15)\
&=x^2-2x-15
end{align*}
$$

We can see that Area from both the cases is the same hence, so we can write it as shown below.

$$
text{Area}=(x-5)cdot(x+3)=x^2+3x-5x-15
$$

For both the parts (a) and (b) the area models are attached below. The given data is shown in the blue colour and the red colour is for the unknown data which is to be obtained.

$textbf{(c)}$ The dimensions for this parts is not unique. There can be more than one possible values for the vertical and horizontal sides. One of the possible values is indicated in the figure of the area model attached below.

$$
text{Area}=(4)cdot(4x^2-6x+1)=16x^2-24+4
$$

$textbf{(d)}$
$$
text{Area}=(3x-2)cdot(x+4)=3x^2+12x-2x-8
$$

$textbf{(a)}$ $text{Area}=6 cdot(13x-21)=78x-126$

$textbf{(b)}$ $text{Area}=(x-5)cdot(x+3)=x^2+3x-5x-15$

$textbf{(c)}$ $text{Area}=(4)cdot(4x^2-6x+1)=16x^2-24+4$

$$
textbf{(d)} text{Area}=(3x-2)cdot(x+4)=3x^2+12x-2x-8
$$

$r$ represents the correlation coefficient here, which can have its value varying between $-1$ to $1$. where $-1$ signifies a perfect linear negative relationship between the variables that means when one variable increases the value of another variable decrease and $+1$ represents a perfect positive relationship between the variables which means that with the increase in one of the variables other variable increases too.

In the given case, to find the association between the number of hours spent watching TV and students’ grade point averages the value of $r$ is equal to $-0.72$ which means that association is negative here.

The student’s grade point will decrease with the increase in the number of the hours spent watching TV. The value is close to $-1$ so we can say the association is close to linear.

In the given case to find the association between the number of hours spent watching TV and students’ grade point averages the value of $r$ is equal to $-0.72$ which means that association is negative here.

The student’s grade point will decrease with the increase in the number of increase in the hours spent watching TV. The value is close to $-1$ so we can say association is close to linear.

a.

$$
7,11,15,19,…..
$$

$$
begin{align*}
a_1&=7\
a_2&=11=a_1+4\
a_3&=15=a_2+4\
a_4&=19=a_3+4
end{align*}
$$

The above given sequence is Arithmetic progression for which common difference $d$ is 4.

b.

As above sequence is A.P with $a_1=7$ and $d=4$ , its nth terms can be written as

$$
t(text{n})=7+(text{n}-1)cdot 4
$$

c.

Lets, assume 109 is a term of the sequence and if we get a natural number value of n then indeed its the term of the sequence otherwise not.

$$
begin{align*}
109&=7+(text{n}-1)cdot 4\
109-7&=(text{n}-1)cdot 4\
text{n}-1&=dfrac{102}{4}\
text{n}&=25.5+1=26.1
end{align*}
$$

26.1 is not a natural number and hence 109 is not a term of sequence.

a. $text{}$ Arithmetic progression

b. $text{}$ $t(text{n})=7+(text{n}-1)cdot 4$

c. $text{}$ 109 is not a term of the given sequence.

We can find the equation of line using the method explained below.

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

Now, we have given points as $(-1,16)$ and $(5,88)$. Let $(x_1,y_1)=(-1,16)$ and $(x_2,y_2)=(5,88)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{88-16}{5-(-1)}\
&=dfrac{72}{6}\
&=12
end{align*}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Therefore, the equation of a line of slope $12$ passing through a point $(-1,16)$ is given by

$$
begin{align*}
y-(16)&=12cdot (x-(-1))\
y-16&=12cdot x +12cdot 1\
y-16&=12cdot x+12\
y&=12cdot x+12+16\
y&=12cdot x+28
end{align*}
$$

We can also rewrite the equation as $f(x)=12x+28$ by replacing $y$ by $f(x)$. Therefore, We can say that the function $f(x)=12x+28$ will work as the correct equation.

Yes, the function $f(x)=12x+28$ will work as the correct equation for the given condition.

Let $l$ represents the length of the rectangle and $w$ represents the width of the rectangle. Given that length is one less than three times its width, so we can represent this as
$$
l=3w-1
$$

Now, as we know that the perimeter of a rectangle is given by
$$
text{Perimeter}=2times (text{Length}+text{Width})
$$

In the question, it is given that the perimeter is 30 inches. so we can represent this information for our case as shown below.

$$
30=2(l+w)
$$

So, we have 2 variable to find and 2 equations which can be solved as mentioned below

$$
begin{align}
l&=3w-1\
30&=2(l+w)
end{align}
$$

We can put the value of $l$ from the equation (1) into the equation (2) which will result in an equation in terms of variable $w$ only, which can be solved to obtain the value of $w$.

$$
begin{align*}
30&=2(l+w)\
30&=2((3w-1)+w)\
30&=2(4w-1) tag{use distributive property}\
30&=8w-2 tag{add 2 to the each side}\
30+2&=8w tag{divide each side by 8} \
dfrac{32}{8}&=w\
w&=4
end{align*}
$$

We can put $w=4$ in the eq(1) to solve for $l$ as shown below.

$$
begin{align*}
l&=3w-1\
l&=3(4)-1\
l&=12-1\
l&=11
end{align*}
$$

Therefore, The rectangle has length equal to $11$ inches and the width equal to $4$ inches.

The rectangle has length equal to $11$ inches and the width equal to $4$ inches.

$textbf{(a)}$
$$
begin{align*}
A&=dfrac{1}{2}bhtag{multiply each side by 2}\
2A &=bh tag{divide each side $b$}\
dfrac{2A}{b}&=dfrac{bh}{b}\
dfrac{2A}{b}&=htag{interchange sides}\
&boxed{h=dfrac{2A}{b}}
end{align*}
$$

$textbf{(b)}$
$$
begin{align*}
x(2x-1)&=2x^2+5x-12tag{use distributive property}\
2x^2-x&=2x^2+5x-12tag{subtract $2x^2$ from each side}\
x&=5x-12tag{add $12-x$ to the each side}\
x+12-x&=5x-x+12-12\
12&=4xtag{divide each side by 4}\
&boxed{x=3}
end{align*}
$$

$textbf{(c)}$

$$
begin{align*}
3x+6y&=24tag{subtract $3x$ from the each side}\
3x-3x+6y&=24-3x\
6y&=24-3xtag{divide each side by 6}\
dfrac{6y}{6}&=dfrac{24-3x}{6}\
&boxed{y=dfrac{24-3x}{6}}
end{align*}
$$

$textbf{(d)}$

$$
begin{align*}
2-3(2x-1)&=-6x+5tag{use distributive property}\
2-6x+3&=-6x+5\
-6x+5&=-6x+5tag{add $6x$ to the each side}\
-6x+6x+5&=-6x+6x+5\
5&=5tag{true always}
end{align*}
$$

The given equation is true for all possible values of $x$ which means $xrightarrow (-infty, +infty)$

$$
textbf{(e)}
$$

$$
begin{align*}
2(5x+z)&=30x+3y+10tag{use distributive property}\
10x+2z&=30x+3y+10tag{subtract $10x+3y$ from each side}\
10x-10x-3y+2z&=30x-10x-3y+3y+10\
-3y+2z&=20x+10tag{subtract 10 from the each side}\
-3y+2z-10&=20xtag{divide each side by 20}\
dfrac{-3y+2z-10}{20}&=dfrac{20x}{20}\
dfrac{-3y+2z-10}{20}&=x\
x&=dfrac{-3y+2z-10}{20}
end{align*}
$$

$textbf{(f)}$

$$
begin{align*}
4x(x+1)&=(2x-3)(2x+5)tag{use distributive property}\
4x^2+4x&=2x^2+10x-6x-15\
4x^2+4x&=2x^2+4x-15tag{subtract $2x^2+4x$ from the each side}\
2x^2&=-15tag{Not possible}
end{align*}
$$

The left side of equation is always positive but the right hand side is negative. So for this equation there is no possible solution.

$textbf{(g)}$

$$
begin{align*}
5(-3+x)&=35tag{use distributive property}\
-15+5x&=35tag{add 15 to the each side}\
5x&=50tag{divide each side by 5}\
x&=dfrac{50}{5}\
&boxed{x=10}
end{align*}
$$

$$
textbf{(h)}
$$

$$
begin{align*}
a&=dfrac{F}{m}tag{multiply each side by $m$}\
am&=dfrac{F}{m}cdot m\
am&=Ftag{divide each side by $a$}\
dfrac{am}{a}&=dfrac{F}{a}\
&boxed{m=dfrac{F}{a}}
end{align*}
$$

$textbf{(i)}$

$$
begin{align*}
ab-2&=3ctag{add 2 to the each side}\
ab&=3c+2tag{divide each side by $a$}\
dfrac{ab}{a}&=dfrac{3c+2}{a}\
&boxed{b=dfrac{3c+2}{a}}
end{align*}
$$

$$
textbf{(j)}
$$

$$
begin{align*}
2(v-3)&=1-(w+4)tag{use distributive property}\
2v-6&=1-w-4\
2v-6&=-3-wtag{add 3 to the each side}\
2v-6+3&=-3+3-w\
2v-3&=-wtag{multiply each side by $-1$}\
-2v+3&=w\
&boxed{w=3-2v}
end{align*}
$$

$textbf{(a)}$ $h=dfrac{2A}{b}$

$textbf{(b)}$ $x=3$

$textbf{(c)}$ $y=dfrac{24-3x}{6}$

$textbf{(d)}$ The given equation is true for all possible values of $x$ which means $xrightarrow (-infty, +infty)$

$textbf{(e)}$ $x=dfrac{-3y+2z-10}{20}$

$textbf{(f)}$ No solution.

$textbf{(g)}$ $x=10$

$textbf{(h)}$ $m=dfrac{F}{a}$

$textbf{(i)}$ $b=dfrac{3c+2}{a}$

$textbf{(j)}$ $w=3-2v$

$textbf{(a)}$
$$
begin{align*}
8x+4y&=2tag{subtarct $8x$ from each side}\
8x-8x+4y&=2-8x\
4y&=2-8xtag{divide each side by 4}\
dfrac{4y}{4}&=dfrac{2-8x}{4}\
y&=dfrac{2-8x}{4}\
&boxed{y=dfrac{1}{2}-2x}
end{align*}
$$

$textbf{(b)}$

$$
begin{align*}
12x-3y&=7tag{subtract $12x$ from the each side}\
12x-12x-3y&=7-12x\
-3y&=7-12xtag{divide each side by $-3$}\
dfrac{-3y}{-3}&=dfrac{7-12x}{-3}\
y&=-(dfrac{7-12x}{3})\
y&=dfrac{12x-7}{3}\
&boxed{y=4x-dfrac{7}{3}}
end{align*}
$$

$textbf{(a)}$ $y=dfrac{1}{2}-2x$

$textbf{(b)}$ $y=4x-dfrac{7}{3}$

$textbf{(a)}$

$$
begin{align*}
8a+a-3&=6a-2a-3\
9a-3&=4a-3tag{subtract $4a$ from the each side}\
9a-4a-3&=4a-4a-3\
5a-3&=-3tag{add 3 to the each side}\
5a&=0tag{divide each side by 5}\
a&=dfrac{0}{5}\
&boxed{a=0}
end{align*}
$$

We can check our solution by putting $a=0$ into the original eaquation and see if it satisfies the equation or not.

$$
begin{align*}
8a+a-3&=6a-2a-3\
8(0)+(0)-3&=6(0)-2(0)-3\
0+0-3&=0-0-3\
-3&=-3tag{true always}
end{align*}
$$

We can see that $a=0$ satisfies the original equation, hence we can say that our solution is valid.

$textbf{(b)}$

$$
begin{align*}
(m+2)(m+3)&=(m+2)(m-2)tag{rearrange}\
(m+2)(m+3)-(m+2)(m-2)&=0tag{take $m+2$ common}\
(m+2){(m+3)-(m-2)}&=0\
(m+2){m-m+3+2}&=0\
(m+2)(5)&=0\
Rightarrow \
m+2&=0tag{subtract $2$ from the each side}\
m+2-2&=0-2\
&boxed{m=-2}
end{align*}
$$

We can verify our result same as the method used in the part (a).

$textbf{(c)}$

$$
begin{align*}
dfrac{x}{2}+1&=6tag{subtract 1 from the each side}\
dfrac{x}{2}+1-1&=6-1\
dfrac{x}{2}&=5tag{multiply each side by 2}\
dfrac{x}{2}cdot 2&=5cdot 2\
&boxed{x=10}
end{align*}
$$

$textbf{(d)}$

$$
begin{align*}
4t-2+t^2&=6+t^2tag{subtact $t^2$ from the each side}\
4t-2+t^2-t^2&=6+t^2-t^2\
4t-2&=6tag{add 2 to the each side}\
4t-2+2&=6+2\
4t&=8tag{divide each side by 4}\
dfrac{4t}{4}&=dfrac{8}{4}\
&boxed{t=2}
end{align*}
$$

$textbf{(a)}$ $a=0$

$textbf{(b)}$ $m=-2$

$textbf{(c)}$ $x=10$

$textbf{(d)}$ $t=2$

$$
begin{align*}text{Rent}&=800+50cdot t\
text{Take-home pay}&=1500+15cdot t tag{text{where t is time in years}}
end{align*}
$$
As we need to find the time when rent equals take-home pay.

$$
begin{align*}Rightarrow
800+50t&=1500+15cdot t\
800-800+50cdot t -15cdot t&=1500-800+15cdot t-15cdot t tag{text{subtracting 800 and $15cdot t$ from each side}}\
35cdot t&=700\
t&=20 text{ years}\
end{align*}
$$

Now, monthly rent for this year will be $800+50cdot 20=1800$ $text{textdollar}$

a.$text{}$ 20 years

b. $text{}$ 1800 $

$textbf{(a)}$ In the hint it is mentioned that the given sequence is arithmetic.
We know that the general term of an arithmetic sequence is given by

$$
t(n)=t(1)+(n-1)d
$$

where, $t(n)$ represents the $n^text{th}$ term of the sequence , $t(1)$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.

We are given $t(1)=1$ and we can put the other given known values of terms into the equations and solve for the value $d$ as shown below.

$$
begin{align*}
t(n&)=(1)+(n-1)d\
t(5)&=1+(5-1)d\
-7&=1+4d\
-8&=4d\
d&=-2
end{align*}
$$

Therefore, the final equation for the given sequence is given by

$$
t(n)=1+(n-1)cdot (-2)
$$

So , we can find $t(23)$ by putting $n=23$ into the final equation.

$$
begin{align*}
t(23)&=1+(23-1)cdot (-2)\
t(23)&=1-22cdot -2\
t(23)&=1-44\
t(23)&=-43
end{align*}
$$

$textbf{(b)}$ This sequence appears to be a geometric sequence for which the general term can be written as

$$
t(n)=t(1)(r)^{n-1}
$$

We have $t(1)=10$ and we can find the common ratio $(r)$ by taking the ratio of any two consecutive terms in order of higher order term is in numerator and lower number term should be in denominator. We can verify the result by checking the value of $r$ for more than one case.

$$
r=dfrac{18}{10}=1.8
$$

$$
r=dfrac{32.4}{18}=1.8
$$

So we can write the equation by putting $t(1)=10$ and $r=1.8$ into the general term of the geometric sequence

$$
t(n)=10(1.8)^{n-1}
$$

So , we can find $t(4)$ by putting $n=4$ into the final equation.

$$
begin{align*}
t(4)&=10(1.8)^{4-1}\
t(4)&=10(1.8)^3\
t(4)&=10(5.832)\
t(4)&=58.32
end{align*}
$$

$textbf{(a)}$ $t(23)=-43$

$textbf{(b)}$ $t(4)=58.32$

$textbf{(a)}$ On applying the transformation function $(xrightarrow -x, y rightarrow y)$ the $x$ coordinates of the given points will get multiplied by -1 and $y$ coordinates will remain the same.

$$
Rightarrow
$$

$$
Y(1,9) rightarrow Y'(-1,9)
$$

$textbf{(b)}$ These set of rigid transformation will take W’X’Y’Z’ back on to WXYZ.
360$text{textdegree}$ rotation along any vertex point followed by the reflection along the $y$ axis.
Although 360$text{textdegree}$ is a redundant operation, but the question required more than one rigid transformation. That is why we can use it as an operation first.

$textbf{(a)}$ $Y(1,9) rightarrow Y'(-1,9)$

$textbf{(b)}$ These set of rigid transformation will take W’X’Y’Z’ back on to WXYZ.
360$text{textdegree}$ rotation along any vertex point followed by the reflection along the $y$ axis.
Although 360$text{textdegree}$ is a redundant operation, but the question required more than one rigid transformation. That is why we can use it as an operation first.

For making the graph of any given line first we need to calculate at least 2 pair of points on the line. Then we can locate these points on the coordinate plane and can easily draw a line passing through them.

We can choose any one coordinate point first and solve for the other by putting that assumed coordinate point into the given equation of the line.

$bullet$ Let’s find the points on the line with equation $y=x+2$

Let’s assume $x=0$ is the $x$ coordinate of the point, now we need to solve for the $y$ coordinate

$$
begin{align*}
y&=x+2\
y&=0+2\
y&=2
end{align*}
$$

Now we have the coordinate of one point as $(0,2)$. Now let’s find out the other point on this line.

Lets $x=-2$ is the $x$ coordinate of the assumed point and putting this into the equation we can solve for the $y$ coordinate.

$$
begin{align*}
y&=x+2\
y&=-2+2\
y&=0
end{align*}
$$

Therefore, the coordinate of the other point on this line is $(-2,0)$.
The graph of the line passing through these points is drawn and attached.

$$
bullet
$$

Similarly, we need to find the two points on the line with the equation $y=2x-1$

Let’s assume $x=0$ then the value of $y$ corresponding to this will be $y=-1$

Now, assume that the $x$ coordinate of the other point on this line is 1 then the $y$ coordinate corresponding to the $x=1$ will be $y=1$

Therefore, the 2 points on the line $y=2x-1$ are $(0,-1)$ and $(1,1)$ and we can easily draw the line through them.

For the point of intersection of the both lines, we substitute the value of $y$ from one equation into the other and this will result in an equation only in terms of $x$ and we can solve for $x$ which will give the $x$ coordinate of the point of intersection. We can use this $x$ in any of the equation to find the $y$ coordinate of the point of intersection.

$$
begin{align}
y&=x+2\
y&=2x-1
end{align}
$$

Substitute value of $y$ from the equation (1) into the equation (2)

$$
begin{align*}
x+2&=2x-1tag{subtract $x$ from the each side}\
2&=x-1tag{add 1 to the each side}\
3&=x\
x&=3
end{align*}
$$

Put $x=3$ into the equation (2), and solve for $y$

$$
begin{align*}
y&=x+2\
y&=3+2\
y&=5
end{align*}
$$

Therefore, we have the point of intersection of the given lines as $(3,5)$

$textbf{(a)}$ First we need to find any two points on the line, then we can locate these points on the graph and then we can easily draw the lines through them. The graph of lines are attached inside.

$textbf{(b)}$ The point of intersection of the given lines is $(3,5)$

Charle’s tree grow 1.5 feet per year and has initial height 3-foot. Let $t$ represents the time in years and $h_C(n)$ represent the height of the Charle’s plant in feet in $n^{text{th}}$ year then we can represent this situation in the form of the equation as shown below.

$$
begin{align*}
h_C(n)=1.5n+3
end{align*}
$$

Now, Amy’s plant has initial height 0 and grows with the rate 1.75 feet per year. Let $h_A(n)$ represent the height of the Amy’s plant in feet in $n^{text{th}}$ year so we can represent this situation in the form of the equation as shown below.

$$
begin{align*}
h_A(n)=1.75n
end{align*}
$$

For finding the time when the height of the plants become equal we need to equate both the equation obtained above that is $h_C(n)=h_A(n)$

$$
Rightarrow
$$

$$
begin{align*}
h_C(n)&=h_A(n)\
1.5n+3&=1.75ntag{subtract $1.5n$ from the each side}\
1.5n-1.5n+3&=1.75n-1.5n\
3&=0.25ntag{use $0.25=dfrac{25}{100}$}\
3&=dfrac{25n}{100}tag{multiply each side by $ dfrac{100}{25}$}\
3cdot dfrac{100}{25}&=dfrac{25n}{100}cdot dfrac{100}{25}\
3cdot 4&=n\
12&=n\
&boxed{n=12}
end{align*}
$$

Yes, the trees will be of same size after 12 years.

The table of values of coordinates on both the equations is attached below.
$h_C(n)=1.5n+3$
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
$h_C(n)$&$n$\
hline
0&3\
hline
6&12\
hline
{color{blue}{
12}}&{color{blue}{
21}}\
hline
18&30\
hline
22&36\
hline
end{tabular}
end{center}

The table of values of coordinates on both the equations is attached below.
$h_C(n)=1.75n$
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
$h_A(n)$&$n$\
hline
0&0\
hline
4&7\
hline
{color{blue}{
12}}&{color{blue}{
21}}\
hline
16&28\
hline
20&35\
hline
end{tabular}
end{center}
The representation by graph is shown below.\

$textbf{(a)}$ Let $y$ represents the height of the plant and $x$ represents the number of years.
Then we can represent the Charle’s equation as $y=1.5x+3$. Each solution of this equation will give coordinates of the $x$ and $y$ which gives the height $y$ of the tree in any year $x$. Therefore, there can be infinite solutions possible for this equation as the $x$ and $y$ can take all positive real values as input and output.

Similarly, we can represent Amy’s equation as $y=1.75x$ and it can also have many solutions which mean, corresponding to each year we will get a unique height. Practically a year can take all real values greater than 0 therefore, the height of the tree can also give all real values greater than 0 as output.

$textbf{(b)}$ The $x$ coordinate of the solution represents the value of the time in the years which can be fractional also. And the $y$ coordinate of the solution represents the height of the tree in feet.

$textbf{(c)}$ There is only a single solution to both Charle’s and Amy’s equation because their lines on the graph intersect each other only at one point (12,21).

$textbf{(a)}$ Many solutions

$textbf{(b)}$ The $x$ coordinate of the solution represents the value of the time in the years which can be fractional also. And the $y$ coordinate of the solution represents the height of the tree in feet.

$textbf{(c)}$ Single solution

$textbf{(a)}$ The main assumption for this model is that we assume that tree’s height remains same throughout the year and changes to a different value with the start of a new year. This assumption cannot be practically true as the trees grow continuously. Also, we assumed that growth per year is the same but practically this also is also environmental factors dependent and hence may not true in real life.

$textbf{(b)}$ The domain in this context represents the number of years which can start from only and cannot be negative and also theoretically it can go up to infinite years but a plants life will be somewhere close to a maximum of 150 to 200 years. Therefore, the domain in this context will be $(0,200)$

The range in this context represents the height of the plant which is initially for Charle’s plant and 0 for Amy’s plant.

The maximum height of any tree can go up to 20 feet or somewhere close to it. So the range for the Charle’s tree is $(3,20)$ and range for Amy’s tree is $(0,20)$

The graph of the lines starts from the $-infty$ and go up to $+infty$ which is not practically true considering the reasoning given above.

$textbf{(a)}$ The main assumption for this model is that we assume that tree’s height remains same throughout the year and changes to a different value with the start of a new year.

$textbf{(b)}$ The domain in this context will be $(0,200)$

The range for the Charle’s tree is $(3,20)$ and range for Amy’s tree is $(0,20)$

Let $y$ represents the SAT scores and $x$ represents the number of weeks with the starting week number is assumed 0.

We can represent George’s situation with the equation shown below.

$$
y=850+10x
$$

We can represent Sally’s situation with the equation shown below.

$$
y=570+50x
$$

$textbf{(a)}$ We need to equate the values of $y$ from both the equations.

$$
begin{align*}
850+10x&=570+50xtag{subtract $570+10x$ from the each side}\
850-570-10x+10x&=570-570-10x+50x\
280&=40xtag{divide each side by 40}\
dfrac{280}{40}&=dfrac{40x}{40}\
7&=x
end{align*}
$$

Therefore, SAT score for Sally and George will be equal on the $7^text{th}$ week.

$textbf{(b)}$ We need to put $x=12$ in both the equations and solve for the value of $y$.

$bullet$ Sally’s SAT score in $12^text{th}$ week

$$
begin{align*}
y&=850+10x\
y&=850+10(12)\
y&=850+120\
y&=970
end{align*}
$$

$bullet$ George’s SAT score in $12^text{th}$ week

$$
begin{align*}
y&=570+50x\
y&=570+50(12)\
y&=570+600\
y&=1170
end{align*}
$$

Hence, George will score higher, if the SAT test is in 12 weeks.

$textbf{(a)}$ SAT score for Sally and George will be equal on the $7^text{th}$ week.

$textbf{(b)}$ George will score higher, if the SAT test is in 12 weeks.

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
-2left(4-3xright)-6x=10& {;}quad : -8+6x-6x=10tag{Expand}\
&-8=10tag{Simplify} \
end{align*}
$$

$$
color{#c34632} text{ No solution }
$$

$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad :aleft(b+cright)=ab+ac
$$

$$
color{#c34632} text{ }a=-2,:b=4,:c=-3x
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
frac{x-5}{-2}=frac{x-1}{-3}& {;}quad : left(x-5right)left(-3right)=left(-2right)left(x-1right)tag{Multiply}\
&-3x+15=-2x+2left(x-1right)tag{Expand} \
&-3x+15-15=-2x+2-15tag{Subtract 15 from both sides} \
&-3x=-2x-13tag{Simplify} \
&-3x+2x=-2x-13+2xtag{Add 2x to both sides } \
&-x=-13tag{Simplify} \
&frac{-x}{-1}=frac{-13}{-1}tag{Divide both sides by -1} \
&{color{#c34632}x=13}
end{align*}
$$

$$
color{#c34632} text{ } mathrm{Apply:fraction:cross:multiply::if:}frac{a}{b}=frac{c}{d}mathrm{:then:}acdot :d=bcdot :c
$$

$$
color{#4257b2} text{ a) No solution }
$$

$$
color{#4257b2} text{ b) }x=13
$$

For drawing graph of any line, we need to find at least two pair of $x$ and $y$ coordinates on this line. For this, we need to assume any one of the coordinate( Let’s say $x$) first and solve for the other coordinate ($y$)by putting the assumed coordinate into the given equation.

$bullet$ For $y=-x+2$

Let $x=0$

$$
begin{align*}
y&=-x+2\
y&=-(0)+2\
y&=2
end{align*}
$$

Therefore, the point is $(0,2)$

Now, for another point on this line, Let $x=2$

$$
begin{align*}
y&=-x+2\
y&=-(2)+2\
y&=0
end{align*}
$$

Therefore, the 2 points on the line $y=-x+2$ are $(0,2)$ and $(2,0)$. We can locate these points on the graph and we can easily draw a stright line through them.

$bullet$ For $y=3x+6$

Let $x=-2$

$$
begin{align*}
y&=3x+6\
y&=3(-2)+6\
y&=-6+6\
y&=0
end{align*}
$$

Therefore, the point is $(-2,0)$

Now, for another point on this line, Let $x=0$

$$
begin{align*}
y&=3x+6\
y&=3(0)+6\
y&=0+6\
y&=6
end{align*}
$$

Therefore, the 2 points on the line $y=3x+6$ are $(-2,0)$ and $(0,6)$. We can locate these points on the graph and we can easily draw a stright line through them.

The intersection point is $(-1,3)$ and we can clearly see from the graph that one of the line is increasing and the other in decreasing. Therefore, it is not possible for both the equation to attain the same value except the point $(-1,3)$ hence we can say that they intersect only at a single point.

For drawing graph of any line, we need to find at least two pair of $x$ and $y$ coordinates on this line. For this, we need to assume any one of the coordinate( Let’s say $x$) first and solve for the other coordinate ($y$)by putting the assumed coordinate into the given equation.
The intersection point is $(-1,3)$ and we can clearly see from the graph that one of the line is increasing and the other in decreasing. Therefore, it is not possible for both the equation to attain the same value except the point $(-1,3)$ hence we can say that they intersect only at a single point.

The $r$ represents the correlation coefficient which has a value 0.89 for the given case. We can say that there is a positive association between the life expectancy of citizen and the average number of TVs in households.

The $r$ value is close to $+1$ which means that the association is close to the strong linear relationship. We can find the $R-squared$ value (coefficient of determination) by squaring $r$.

$$
Rightarrow R^2=0.89^2=0.7921
$$

Now, $R^2=0.792$ signifies that almost 79 % variation in the life expectancy can be predicted by the number of TVs in households and rest 21% variation is dependent on the other factors.

So, we can say that watching TV helps us live longer.

We can say that there is a positive association between the life expectancy of citizen and the average number of TVs in households.
$R^2=0.792$ signifies that almost 79 % variation in the life expectancy can be predicted by the number of TVs in households and rest 21% variation is dependent on the other factors.

$textbf{(a)}$ Given that $a_1=17$ and the recursive equation is $a_{n+1}=a_n-3$

$$
begin{align*}
a_1&=17\
a_2&=a_1-3=14=17-3=17-3cdot 1=17-3cdot (2-1)\
a_3&=a_2-3=11=17-3-3=17-3cdot 2=17-3cdot (3-1)\
a_4&=a_3-3=9=17-3-3-3=17-3cdot 3=17-3cdot (4-1)\
a_n&=a_{n-1}-3=17-3cdot (n-1)
end{align*}
$$

Therefore, the explicit equation for this case is given by
$$
boxed{a_n=17-3cdot (n-1)}
$$
The few terms of the sequence are $17, 14, 11, 9, cdots$

$textbf{(b)}$ Given that $a_1=20$ and the recursive equation is $a_{n+1}=dfrac{1}{2}cdot a_n$

$$
begin{align*}
a_1&=20\
a_2&=dfrac{1}{2}cdot a_1=10=dfrac{1}{2}cdot 20=(dfrac{1}{2})^{2-1}cdot 20\
a_3&=dfrac{1}{2}cdot a_2=5=dfrac{1}{2}cdot (dfrac{1}{2}cdot 20)=(dfrac{1}{2})^{3-1}cdot 20\
a_4&=dfrac{1}{2}cdot a_3=2.5=dfrac{1}{2}cdot ((dfrac{1}{2} )^{2}cdot 20)=(dfrac{1}{2})^{4-1}cdot 20\
a_n&=(dfrac{1}{2})^{n-1}cdot 20
end{align*}
$$

Therefore, the explicit equation for this case is given by
$$
boxed{a_n=(dfrac{1}{2})^{n-1}cdot 20}
$$

The few terms of the sequence are $20, 10, 5, 2.5, cdots$

$textbf{(a)}$ $a_n=17-3cdot (n-1)$

$textbf{(b)}$ $a_n=(dfrac{1}{2})^{n-1}cdot 20$

$textbf{(a)}$

$$
begin{align*}
4^x&=(dfrac{1}{2})^{x-9}tag{use $(dfrac{1}{a})^m=a^{-m}$}\
4^x&=2^{-(x-9)}tag{write $4=2^2$}\
(2^2)^x&=2^{-x+9}tag{use $(a^m)^n=a^{mcdot n}$}\
2^{2cdot x}&=2^{9-x}tag{equate the power as base are same}\
2x&=9-xtag{add $x$ to the each side}\
2x+x&=9-x+x\
3x&=9tag{divide each side by 3}\
dfrac{3x}{3}&=dfrac{9}{3}\
&boxed{x=3}
end{align*}
$$

$textbf{(b)}$

$$
begin{align*}
dfrac{x+3}{x}+2&=dfrac{x+5}{x}tag{multiply each side by $x$}\
dfrac{x+3}{x}cdot x+2cdot x&=dfrac{x+5}{x}cdot x\
x+3+2x&=x+5\
3x+3&=x+5tag{subtract $x+3$ from the each side}\
3x-x+3-3&=x-x+5-3\
2x&=2tag{divide each side by 2}\
dfrac{2x}{2}&=dfrac{2}{2}\
&boxed{x=1}
end{align*}
$$

$textbf{(a)}$ $x=3$

$textbf{(b)}$ $x=1$

$textbf{(a)}$
Let $z=$ Zola’s rate of pay (dollars/hour)

$$
2timestext{ pay rate }+$12 text{ bonus}=$ 30
$$

$textbf{(b)}$ Let $z=$ total number of working hours of Zach (in hours)

$$
$12(text{(Zach’s pay rate)})times text{ Zach’s working hours}+ $5text{(Eddie’s pay rate)} times text{ Eddie’s working hours}=$30
$$

$textbf{(c)}$ Let $z=$ number of zebras in the zoo

$$
text{number of zebras }+text{number of elephants } +text{number of monkeys}=30
$$

$textbf{(d)}$ Let $z=$ amount of zinc needed to create a metal (in ounces )

$$
text{amount of zinc}+text{amount of silver}=30
$$

$textbf{(a)}$
Let $z=$ Zola’s rate of pay (dollars/hour)

$textbf{(b)}$ Let $z=$ total number of working hours of Zach (in hours)

$textbf{(c)}$ Let $z=$ number of zebras in the zoo

$textbf{(d)}$ Let $z=$ amount of zinc needed to create a metal (in ounces )

$textbf{(a)}$ Given that the number of cans was one more than four times the number of bottles. We can represent $2.18 as 218textcent . Let$x$represents the number of bottles, then we can represent the situation as shown below.$ $boxed{12cdot x+ 10cdot (4x+1)=218}$
$$
\
textbf{(b)}
begin{align*}
12cdot x+ 10cdot (4x+1)&=218\
12x+40x+10&=218\
52x+20&=218tag{subtract $10$ from the each side}\
52x&=208tag{divide each side by 52}\
x&=dfrac{208}{52}\
&boxed{x=4}
end{align*}
Therefore, Elsie had 4 bottles and
$$
4cdot 4+1=17$cans.\\
textbf{(c)} Let$b$represents the number of bottles and$c$represents the number of cans.
We have been given a relation between$b$and$c$c=4cdot b+1$ $The total earning in terms of$b$and$c$can be represented as$ $12cdot b+ 10 cdot c=218$$
So, we have 2 set of equations as

$$
begin{align}
c=4b+&1\
12b+10c&=218
end{align}
$$

$textbf{(d)}$ Yes, Solomon’s equation and Marcus’s equations represent the same problem. The mathematical modeling can vary person to person but the final answer for both the cases will be same.
We can obtain the identical equation in a single variable by replacing one of the variable ($b$ or $c$) using substitution method in one of the equations by using the other.

$textbf{(e)}$ We obtained that the number of bottles were 4 and number of cans were 17. So we have $b=4$ and $c=17$.

We can verify each equation by putting these values and checking if it holds true or not.

$$
begin{align*}
c&=4b+1\
(17)&=4(4)+1\
17&=16+1\
17&=17tag{true}
end{align*}
$$

$$
begin{align*}
12b+10c&=218\
12(4)+10(17)&=218\
48+170&=218\
218&=218tag{true}
end{align*}
$$

$textbf{(a)}$ $12cdot x+ 10cdot (4x+1)=218$

$textbf{(b)}$ Elsie had 4 bottles and $4cdot 4+1=17$ cans.

$textbf{(c)}$
$$
begin{align}
c=4b+&1\
12b+10c&=218
end{align}
$$

$textbf{(d)}$ Yes, Solomon’s equation and Marcus’s equations represent the same problem. The mathematical modeling can vary person to person but the final answer for both the case, will be the same.

$bullet$ Solomon’s earning

Let $y$ represents the Amount of earning (in dollars) and $x$ represents the amount of recyclable electronics (in pounds)

$$
y=1.5x-27
$$

$bullet$ Marcus’s earning

Let $y$ represents the Amount of earning (in dollars) and $x$ represents the amount of recyclable household appliances (in pounds)

$$
y=0.6x
$$

For evaluating the amount of waste for which they both make the same amount of money, we need to equate the $y$ of both the equation.

$$
begin{align*}
1.5x-27&=0.6xtag{add 27 to the each side}\
1.5x&=0.6x+27tag{subtract $0.6x$ from the each side}\
1.5x-0.6x&=27\
0.9x&=27tag{divide each side by 0.9}\
x&=dfrac{27}{0.9}\
x&=dfrac{27}{9/100}\
x&=dfrac{27}{9}cdot 100\
x&=300
end{align*}
$$

Therefore, they need to recycle 300 pounds each to earn the same amount of money.

We can use the formula $text{Distance}=text{Speed}times text{Time}$ for solving the given questions.

$textbf{(a)}$ Given that the speed of the Morgan was 16 miles per hour and time taken by her was 1.5 hours.

$$
Rightarrow
$$

$$
begin{align*}
text{Distance}&=text{Speed}times text{Time}\
&=16left (dfrac{text{ miles}}{ 1 text{hour}}right)times 1.5 left ( text{ hour} right )\
&=16times 1.5 text{ miles}\
&=24 text{ miles}
end{align*}
$$

$textbf{(b)}$ Given that the speed of the Morgan’s dad was 20 miles per hour and time taken by him was 0.4 hours.

$$
Rightarrow
$$

$$
begin{align*}
text{Distance}&=text{Speed}times text{Time}\
&=20left (dfrac{text{ miles}}{ 1 text{hour}} right) times 0.4 left( text{ hour}right )\
&=20times 0.4 text{ miles}\
&=8 text{ miles}
end{align*}
$$

$textbf{(c)}$ Given that the speed of the Morgan’s dad while jogging was 4.8 miles per hour and time taken by him was 1 hour and 15 minutes

First we need to convert the time in hours. We know that 1 hour is equal to 60 minutes. therefore, 15 minutes is equal to $dfrac{15}{60}=0.25$ hours.
Hence the total time taken by his dad while jogging is $1+0.25=1.25$ hours

$$
Rightarrow
$$

$$
begin{align*}
text{Distance}&=text{Speed}times text{Time}\
&=4.8left (dfrac{text{ miles}}{ 1 text{hour}} right)times 1.25 ( text{ hour})\
&=4.8times 1.25 text{ (miles)}\
&= 6 text{ miles}
end{align*}
$$

$textbf{(a)}$ 24 miles

$textbf{(b)}$ 8 miles

$textbf{(c)}$ 6 miles

$textbf{(a)}$ The three units of measure used in problem 6-35 which were common to all its parts are Distance, Speed and Time.

$textbf{(b)}$
$$
text{Distance}=text{Speed}times text{Time}
$$

$textbf{(c)}$ We can rewrite the relationship in the part (b) as

$$
text{Time}=dfrac{text{Distance}}{text{Speed}}
$$

Now, given that the average speed is $65$ miles per hour and the distance is $195$ miles.

$$
Rightarrow
$$

$$
begin{align*}
text{Time}&=dfrac{text{Distance}}{text{Speed}}\
text{Time}&=dfrac{195}{65}\
&=3 text{ hours}
end{align*}
$$

$textbf{(d)}$ The apparant speed of the puppy will be $44-27=17$ feet per minute upstream.
It can be understood by the diagram ataached below.
Now the Disatnce in travelled by puppy can be found out by applying the formula given in the part (a).

$$
begin{align*}
text{Distance}&=text{Speed}times text{Time}\
&=17 (dfrac{text{feet}}{text{minute}}) times 8 (text{minutes})\
&=17times 8 (text{ feet})\
&=136 text{ feet}
end{align*}
$$

$textbf{(e)}$ The Formula $text{Distance}=text{Speed}times text{Time}$ can be verified using dimensional analysis.

Distance has $L$ dimension , Speed has $dfrac{L}{T}$ dimension and Time has $T$ dimension. So putting all this into the equation we obtain

$$
begin{align*}
text{Distance}&=text{Speed}times text{Time}\
L&=dfrac{L}{T}times T\
L&=Ltag{true}
end{align*}
$$

$textbf{(a)}$ The three units of measure used in problem 6-35 which were common to all its parts are Distance, Speed and Time.

$textbf{(b)}$
$$
text{Distance}=text{Speed}times text{Time}
$$

$textbf{(c)}$ 3 hours

$textbf{(d)}$ 136 feet

$textbf{(e)}$ The equation can be dimensionally verified by putting dimesions of each of the quantity into the equation. If we get equal dimesions on the both side of the equation then equation will be considered as the dimesionally true.

Given that there is $5 setup fee for kayak and then kayak are rented at $8 per hour. Let$y$represents the total cost for renting a kayak and$x$represents the time for which kayak is rented then the given situation can be represented by the equation shown below.$ $boxed{y=8x+5}$ $\
Now, Setup fee for the Canoe rentals is $9 and the per unit hour cost is $6 (from the table). Let$y$represents the total cost of renting Canoe and$x$represents the time for which Canoe is rented then the given situation can be represented by the equation shown below.$ $boxed{y=6x+9}$ $For finding the number of hours when both the rentals cost the same amount we need to equate the$y$ of both the equations.

$$
begin{align*}
8x+5&=6x+9tag{subtract $6x+5$ from the each side}\
8x-6x+5-5&=6x-6x+9-5\
2x&=4tag{divide each side}\
x&=2
end{align*}
$$

Therefore, At 2 hours the cost of both canoe and kayak rentals will be the same amount($21). We can see from the graph attached below that the cost of canoe rentals becomes cheaper than the kayak rentals for the time greater than 2 hours. The canoe equation is graphed in green color and the kayak equation is in red.

The equation for kayak renting is $y=8x+5$ and equation for the cost of canoe renting is $y=6x+9$

At 2 hours the cost of both canoe and kayak rentals will be the same amount($21). We can see from the graph attached inside, that the cost of canoe rentals becomes cheaper than the kayak rentals for the time greater than 2 hours.

$textbf{(a)}$ The unit of $x$ is missing which is an essential part of the statement to make it complete. The complete and correct statement should be ” Let $x$ represent the length of Side #1 in centimeters.

It is given in the question that the Side #1 and side#2 are equal, therefore the length of the side #2 will also be $x$ centimeters.
Given that side #3 is one centimeter shorter than twice the length of Side #1 which means that the length of the side #3 is $2x-1$ centimeters.

$textbf{(b)}$
$$
x+x+(2x-1)=31
$$

$textbf{(c)}$
$$
begin{align*}
x+x+(2x-1)&=31\
4x-1&=31tag{add 1 to the each side}\
4x-1+1&=31+1\
4x&=32tag{divide each side by 4}\
dfrac{4x}{4}&=dfrac{32}{4}\
x&=8
end{align*}
$$

Therefore, the length of the sides are as follows

side #1 $rightarrow$ 8 cm

side #2 $rightarrow$ 8 cm

side #3 $rightarrow$ $2cdot 8-1=15$ cm

$textbf{(a)}$ The unit of $x$ is missing which is an essential part of the statement to make it complete.

$textbf{(b)}$ $x+x+(2x-1)=31$

$textbf{(c)}$ side #1 $rightarrow$ 8 cm

side #2 $rightarrow$ 8 cm

side #3 $rightarrow$ $2cdot 8-1=15$ cm

It is given that the Earth travels 584 million miles in the one year which is an equivalent statement with The Earth travels 584 million miles in 365 days. So we can obtain the speed of the earth in miles per day by dividing the $584times 10^6$ miles (distance) by 365 days( time ) by using the formula.

$$
text{speed}=dfrac{text{distance}}{text{time}}
$$

$$
begin{align*}
text{speed}&=dfrac{584times 10^6}{365}\
text{speed}&=1.6times 10^6 dfrac{text{miles}}{text{day}}
end{align*}
$$

We have 24 hours in a day. So in 365 days, the number of hours will be $365times 24=8760$ hours.

So we can say that the Earth travels $584times 10^6$ miles in 8760 hours. So distance travel by the earth in an hour can be found out by dividing the total distance by the total number of hours took to reach it.

$$
text{speed}=dfrac{584times 10^6}{8760}=6.667times 10^4 dfrac{text{miles}}{text{hour}}
$$

$textbf{(a)}$ $text{speed}=1.6times 10^6 dfrac{text{miles}}{text{day}}$

$textbf{(b)}$ $text{speed}=6.667times 10^4 dfrac{text{miles}}{text{hour}}$

$$
begin{align*}
5(2x-1)-3x&=5x+9tag{use distributive property}\
10x-5-3x&=5x+9\
7x-5&=5x+9 tag{subtract $5x$ from the each side}\
2x-5&=9 tag{add 5 to the each side}\
2x&=14 tag{divide each side by 2}\
x&=7
end{align*}
$$

So, the correct solution is $x=7$. She made the mistake in the third line of her solution where she missed to change the signs while changing the sides of the term.

The correct solution is $x=7$. She made the mistake in the third line of her solution where she missed to change the signs while changing the sides of the term.

Given sequence is $5, 25, 125, 625, cdots$

$textbf{(a)}$ We can observe that each next term of this sequence can be obtained by multiplying the previous terms by 5.This kind of sequence is called a geometric sequence. Where $r$ is the common ratio, which can be obtained by taking ratio of any two consecutive terms such as $r=dfrac{t(n+1)}{t(n)}$ and the expression for the general term of any geometric sequence is given by
$$
t(n)=t(1)cdot (r)6^{n-1}
$$

The common ratio $r$ for this case is $dfrac{25}{5}=5$

$textbf{(b)}$ Fifth term of this sequence can be found out by multiplying the fourth term (625) by 5.

$Rightarrow$
$$
t(5)=5cdot t(4)=5cdot 625=3125
$$

$textbf{(c)}$ The explicit equation can be obtained by putting value of $t(1)$ and $r$ into the general term expression of the geometric sequence.

$$
Rightarrow
$$

$$
t(n)=t(1)cdot (r)6^{n-1}=5cdot 5^{n-1}
$$

$textbf{(a)}$ Geometric sequence

$textbf{(b)}$ 3125

$textbf{(c)}$ $5cdot 5^{n-1}$

Two perpendicular lines have the product of their slopes equal to $-1$. We will be determining the slope of every given line and then we will calculate the product of its slope with the slope of the line $y=-dfrac{2}{3}+5$

If the product is equal to $-1$ then the line is perpendicular to $y=-dfrac{2}{3}x+5$ otherwise it is not.

Now, the general equation of any line is given by $y=mx+c$ where $m$ represents the slope of the line. So we will try to rearrange each given line in the general form so that we can easily compare and calculate the slope of the line.

The given equation of the line is $y=-dfrac{2}{3}x+5$, on comparing it with $y=mx+c$, we can say that the slope of this line is equal to $-dfrac{2}{3}$

$textbf{(a)}$
$$
begin{align*}
2x-3y&=6\
2x&=3y+6\
2x-6&=3ytag{divide each side by 3}\
dfrac{2x}{3}-dfrac{6}{3}&=dfrac{3y}{3}\
dfrac{2}{3}x-2&=y\
y&=dfrac{2}{3}x-2
end{align*}
$$

On comparing it with $y=mx+c$, we can see its slope is $dfrac{2}{3}$.

The product of slopes is $-dfrac{2}{3}times dfrac{2}{3}=-dfrac{4}{9}ne-1$, therefore the line $2x-3y=6$ is not perpendicular to the line $y=-dfrac{2}{3}x+5$

$textbf{(b)}$

$$
begin{align*}
2x+3y&=6\
3y&=-2x+6\
dfrac{3y}{3}&=-dfrac{2x}{3}+dfrac{6}{3}\
y&=-dfrac{2}{3}x+2
end{align*}
$$

The slope of the line $2x+3y=6$ is $-dfrac{2}{3}$

Now, the product of the slopes is $-dfrac{2}{3}times -dfrac{2}{3}=dfrac{4}{9}ne-1$, therefore the line $2x+3y=6$ is not perpendicular to the line $y=-dfrac{2}{3}x+5$

$textbf{(c)}$
$$
begin{align*}
3x-2y&=6\
-2y&=-3x+6tag{divide each side by $-2$}\
dfrac{-2y}{-2}&=dfrac{-3x}{-2}+dfrac{6}{-2}\
y&=dfrac{3}{2}x-3
end{align*}
$$

The slope of the line $3x-2y=6$ is $dfrac{3}{2}$

Now, the product of the slopes is $-dfrac{2}{3}times dfrac{3}{2}=-1$, hence the line $3x-2y=6$ is perpendicular to the line $y=-dfrac{2}{3}x+5$

$textbf{(d)}$
$$
begin{align*}
3x+2y&=6\
2y&=-3x+6tag{divide each side by $2$}\
dfrac{2y}{2}&=dfrac{-3x}{2}+dfrac{6}{2}\
y&=-dfrac{3}{2}x+3
end{align*}
$$

The slope of the line $3x+2y=6$ is $-dfrac{3}{2}$

Now, the product of the slopes is $-dfrac{2}{3}times -dfrac{3}{2}=1ne-1$, hence the line $3x+2y=6$ is not perpendicular to the line $y=-dfrac{2}{3}x+5$

Among the given lines the only line perpendicular to the given line is
$$
3x-2y=6
$$
because these have the product of their slopes equal to $-1$.

The slope triangle is drawn and attached below. The slope of the line is given by $tantheta$ which is here, is equal to $dfrac{Delta y}{Delta x}=dfrac{-1-6}{5-3}=-dfrac{7}{3}$

The slope triangle is a right-angled triangle in which we can apply the Pythagoras theorem to find any unknown side (Segment AC)

$$
text{hypotenuse}=sqrt{text{base}^2+text{perpendicular height}^2}
$$

$$
text{Length AC}=sqrt{3^2+7^2}=sqrt{58}
$$

Slope $=-dfrac{7}{3}$ and Length of segment AC is $sqrt {58}$ units.

$bullet$ Case of Team Sunshine

Let $y$ represents the amount of water in the kiddie pool (in gallons) and $x$ is the time (in minutes).

Given that the pool has 30 gallons in it and Team Sunshine is adding 8 gallons per minute with a garden hose. So we can represent this situation by the equation
$$
y=8x+30
$$

$bullet$ Case of Team Breeze

Let $y$ represents the amount of water in the Team Breeze’s pool (in gallons) and $x$ is the time (in minutes).

Given that the pool initially has180 gallons in it and Team is emptying the pool at the rate of 8 gallons per minute with buckets. So we can represent this situation by the equation
$$
y=180-5x
$$

To find the time when both the pools have the same amount of water, we need to equate the $y$ of both the equations.

$$
Rightarrow
$$

$$
begin{align*}
8x+30&=180-5xtag{add $5x$ to the each side}\
8x+5x+30&=180-5x+5x\
13x+30&=180tag{subtract 30 from the each side}\
13x&=150tag{divide each side by 13}\
x&=dfrac{150}{13}\
x&=11.54 text{ minutes}
end{align*}
$$

Therefore, the amount of water will be equal in both the pool after 11.54 minutes.

$textbf{(a)}$ It is given that $t$ represent the unknown time in hours that it took the hare to complete the race. The tortoise takes 8 hours longer than the hare to finish the race.

$$
Rightarrow
$$

$$
text{Time taken by tortoise}=t+8
$$

$textbf{(b)}$ Let $y$ represents the total distance of the race.

$bullet$ Case of hare

Given that the hare moves 250 feet per hour and time taken by the hare is $t$ hours

$$
y=250t
$$

$bullet$ Case of tortoise

Given that the tortoise moves 50 feet per hour and time taken by the hare is $t+8$ hours

$$
y=50(t+8)
$$

$textbf{(c)}$ We have set of 2 equations

$$
begin{align}
y&=250t\
y&=50(t+8)
end{align}
$$

we can substitute the $y$ from the equation (1) into the equation (2)

$$
Rightarrow
$$

$$
begin{align*}
250t&=50(t+8)\
250t&=50t+400tag{subtract 50t from the each side}\
250t-50t&=50t-50t+400\
200t&=400tag{divide each side by 200}\
dfrac{200t}{200}&=dfrac{400}{200}\
t&=2
end{align*}
$$

Now put $t=2$ in the equation (1) , and solve for $y$

$$
begin{align*}
y&=250t\
y&=250(2)\
y&=500 text{ feet}
end{align*}
$$

therefore, The distance of the race is 500 feet.

$textbf{(a)}$ $t+8$

$textbf{(b)}$

$$
y=250t
$$

$$
y=50(t+8)
$$

$textbf{(c)}$ The distance of the race is 500 feet.

First we need to rearrange the equation $x-2y=4$ in “$y=$” form.

$$
begin{align*}
x-2y&=4tag{subtract $x$ from the each side}\
-2y&=4-x tag{divide each term by $-2$}\
dfrac{-2y}{-2}&=dfrac{4}{-2}+dfrac{-x}{-2}\
y&=-2+dfrac{1}{2}x\
y&=dfrac{1}{2}x-2
end{align*}
$$

Therefore, now we have 2 sets of equations

$$
begin{align}
y&=dfrac{1}{2}x-2\
y&=-dfrac{1}{2}x+4
end{align}
$$

Add both the equation (1) and equation (2), and solve for resulting equation in single variable $y$

$$
begin{align*}
y+y&=(dfrac{1}{2}x-2)+(-dfrac{1}{2}x+4)\
2y&=2tag{divide each side by 2}\
y&=1
end{align*}
$$

Put $y=1$ in the equation (2) and solve for $x$

$$
begin{align*}
(1)&=-dfrac{1}{2}x+4\
1-4&=-dfrac{1}{2}x\
-3cdot 2&=-x\
-6&=-x\
x&=6
end{align*}
$$

So, the solution point is $(6,1)$ and we can verify the solution by putting the solution point in the original equations and check if it satisfies the equation or not.

$$
begin{align*}
x-2y&=4\
(6)-2(1)&=4\
6-2&=4\
4&4tag{holds true}
end{align*}
$$

Therefore, the solution point $(6,1)$ is valid for th equation $x-2y=4$

$$
begin{align*}
y&=-dfrac{1}{2}x+4\
(1)&=-dfrac{1}{2}(6)+4\
1&=-3+4\
1&=1tag{holds true}
end{align*}
$$

The solution point $(6,1)$ is also valid for the equation $y=-dfrac{1}{2}x+4$. Hence, we can say that our solution point is valid.

The solution point is $(6,1)$ and it satisfies both the original equations while checking.

The equation $x+2y=14$ can be rearraged to write it as $x=-2y+14$ and the equation $-x+3y=26$ can be rewritten as $x=3y-26$.

Now as we have both the equation in $x=$ form then we can apply the equal values method on the variable $x$. The solution can be proceeded as shown below

$$
begin{align*}
-2y+14&=3y-26tag{add $2y$ to the each side}\
14&=3y+2y-26tag{add 26 to the each side}\
14+26&=5y\
40&=5ytag{divide each side by 5}\
dfrac{40}{5}&=dfrac{5y}{5}\
8&=y\
y&=8
end{align*}
$$

Now, put $y=8$ into equation $x=-2y+14$ to solve for the value of $x$

$$
begin{align*}
x&=-2y+14\
x&=-2(8)+14\
x&=-16+14\
x&=-2
end{align*}
$$

Therefore, The solution point for the given equations is $(-2,8)$. We can check this solution by putting the solution point $(-2,8)$ into the original equation to see if it satisfies or not.

$bullet$ Checking validity of $(-2,8)$ into $x+2y=14$

$$
begin{align*}
x+2y&=14\
(-2)+2(8)&=14\
-2+16&=14\
14&=14tag{true}
end{align*}
$$

$bullet$ Checking validity of $(-2,8)$ into $-x+3y=26$

$$
begin{align*}
-x+3y&=26\
-(-2)+3(8)&=26\
2+24&=26\
26&=26tag{true}
end{align*}
$$

Therefore, The solution for the given equations is $(-2,8)$.

The solution for the given equations is $(-2,8)$

$textbf{(a)}$ Given that $c$ represents the number of children and $a$ represents the adults which attended the performance. Total 150 people attended the performance at the school auditorium.
We can write the equation for the given situation as shown below.

$$
c+a=150
$$

$textbf{(b)}$ Given that total expenditure by Wade on the CDs and video games was $84.84. Let$c$represent the number of CDs and$v$represents the number of a video games he bought. Given that cost of a new CD is $14.95 and cost of a video game is $39.99.\
The equation for this situation can be written as shown below$ $14.95c+39.99v=84.84$$

$textbf{(a)}$ $c+a=150$

$textbf{(b)}$ $14.95c+39.99v=84.84$

The total distance between Jonanthan and Laura is 3 miles. Given that they are travelling towards each other, so if Jonathan travels m miles from the total distance of 3 miles than the distance travelled by Laura will be $3-m$ miles. The situation is represented by a figure attached below.

$3-m$ miles

$textbf{(a)}$
$$
begin{align*}
y&=2x-5tag{add 5 to the each side}\
y+5&=2x-5+5\
y+5&=2xtag{divide each side by 2}\
dfrac{y+5}{2}&=dfrac{2x}{2}\
dfrac{y+5}{2}&=x\
&boxed{x=dfrac{y+5}{2}}
end{align*}
$$

$textbf{(b)}$

$$
begin{align*}
p&=-aw+9tag{subtract 9 from the each side}\
p-9&=-aw+9-9\
p-9&=-awtag{divide each side by $-a$}\
dfrac{p-9}{-a}&=dfrac{-aw}{-a}\
dfrac{p-9}{-a}&=w\
&boxed{w=dfrac{9-p}{a}}
end{align*}
$$

$textbf{(c)}$

$$
begin{align*}
2m-6&=4n+4tag{add 6 to the each side}\
2m-6+6&=4n+4+6\
2m&=4n+10tag{divide each side by 2}\
dfrac{2m}{2}&=dfrac{4n}{2}+dfrac{10}{2}\
&boxed{m=2n+5}
end{align*}
$$

$textbf{(d)}$

$$
begin{align*}
bx-y&=-2ytag{add $y$ to the ecah side}\
bx-y+y&=-2y+y\
bx&=-ytag{multiply each side by $-1$}\
bxcdot -1&=-ycdot -1\
-bx&=y\
&boxed{y=-bx}
end{align*}
$$

$textbf{(a)}$ $x=dfrac{y+5}{2}$

$textbf{(b)}$ $w=dfrac{9-p}{a}$

$textbf{(c)}$ $m=2n+5$

$textbf{(d)}$ $y=-bx$

We know that there are 52 weeks in one year. So to find the number of years equivalent to 260 weeks we can use Giant Ones method shown below.

$$
begin{align*}
text{No. of years}&= 260 text{ weeks} cdot dfrac{text{1 year}}{text{52 weeks}}\
&=(dfrac{260}{52})(dfrac{text{weeks}}{text{weeks}})(text{years})\
&=5 text { years}
end{align*}
$$

So it will take 5 years to Sam, to receive the full interest.

$textbf{(a)}$ $a_n= 2n-5$

$$
begin{align*}
a_1&=2cdot 1-5=2-5=-3\
a_2&=2cdot 2-5=4-5=-1\
a_3&=2cdot 3-5=6-5=1\
a_4&=2cdot 4-5=8-5=3\
a_5&=2cdot 5-5=10-5=5
end{align*}
$$

$textbf{(b)}$ $a_1 =3$ and $a_{n+1} =-2cdot a_n$

$$
begin{align*}
a_1&=3\
a_2&=-2cdot a_1=-2cdot 3=-6\
a_3&=-2cdot a_2=-2cdot -6=12\
a_4&=-2cdot a_3=-2cdot 12=-24\
a_5&=-2cdot a_4=-2cdot -24=48\
end{align*}
$$

$textbf{(a)}$ $(-3,-1,1,3,5)$

$textbf{(b)}$ $(3,-6,12,-24,48)$

$$
begin{align}
y=-x-7\
5y+3x&=-13
end{align}
$$

We can rearrange the equation (2) in the $y=$ form so that we can use equal value method with equation (1) which we learned so far. In the equal value method we obtain both the equations in the form of $y=$ only or in form of $x=$ only, so that we can equate both the expression corresponding to that $y$ or $x$.

$bullet$ rearranging the equation (2)

$$
begin{align*}
5y+3x&=-13tag{subtract $3x$ from the each side}\
5y&=-3x-13tag{divide each term by 5}\
y&=-dfrac{3x}{5}-dfrac{13}{5}
end{align*}
$$

Now, we use equal value method for equation (1) and $y=-dfrac{3x}{5}-dfrac{13}{5}$

$$
Rightarrow
$$

$$
begin{align*}
-x-7&=-dfrac{3x}{5}-dfrac{13}{5}tag{add $x$ to the each side}\
-x+x-7&=x-dfrac{3x}{5} -dfrac{13}{5}\
-7&=dfrac{5x-3x}{5} -dfrac{13}{5}tag{add $dfrac{13}{5}$ to the each side}\
-7+dfrac{13}{5}&=dfrac{2x}{5} \
dfrac{-35+13}{5}&=dfrac{2x}{5} tag{multiply each side by 5}\
-22&=2xtag{divide each side by 2}\
-11&=x
end{align*}
$$

Now , put $x=-11$ into the equation (1) and solve for $y$

$$
begin{align*}
y&=-x-7\
y&=-(-11)-7\
y&=11-7\
y&=4
end{align*}
$$

The solution point for the given equations is $(-11,4)$. We could have solved the given set of equations more easily by using substitution method. But as the question required us to solve it using the equal value method that is why it is a bit tedious.

The solution point for the given equations is $(-11,4)$.

$textbf{(a)}$ Yes, we can switch the y and the $- x – 7$ as they are equal as per given equation $y =-x -7$.

$textbf{(b)}$ Yes, we can replace the variable $y$ with $- x – 7$ in the other equation, if we want to find their point or intersection or so called solution for the given pair. It is just like replacing the value of $y$ with a constant but not in this case.

$textbf{(c)}$ The resultant of the substitution is $5(-x-7)+3x=-13$. we can solve it as shown below.

$$
begin{align*}
5(-x-7)+3x&=-13\
-5x+3x-35&=-13\
-2x&=-13+35\
-2x&=22\
x&=dfrac{22}{-2}\
x&=-11
end{align*}
$$

Using the value $x=-11$, we can solve for $y$ by putting it into $y =-x -7$, as shown below

$$
begin{align*}
y&=-1times -11 -7\
y&=11-7\
y&=4\
end{align*}
$$

$textbf{(a)}$ Yes, we can switch the y and the $- x – 7$.

$textbf{(b)}$ Yes.

$textbf{(c)}$ $(x,y)=(-11,4)$

The speed of bharat is 12 kilometers per hour and the speed of Ingrid is 14 kilometers per hour.

The formula relating distance, speed and time is
$$
text{Distance}=text{Speed}times text{Time}
$$

$textbf{(a)}$ If Bharat rides a distance of $b$ kilometers, then time taken by him to ride this distance is given by

$$
text{Time}=dfrac{text{Distance}}{text{speed}}=dfrac{b}{12} text{ hours}
$$

Now, with the speed $14$ kilometers per hour Ingid can ride the distance in this time

$$
begin{align*}
text{Distance}&=text{Speed}times text{Time}\
&=14 times dfrac{b}{12}\
&=dfrac{14b}{12}\
&=boxed{dfrac{7b}{6}}
end{align*}
$$

$textbf{(b)}$ Let $d_b$ represents the distance travelled by Bharat after any time $t$ in hours.

$Rightarrow$

$$
d_b=12times t
$$

Let $d_i$ represents the distance travelled by Ingrid after any time $t$ in hours.

$Rightarrow$

$$
d_i=14times t
$$

We need to find the time when the distance between them becomes 78 kilometers. We can represent this situation by the equation shown below.

$$
begin{align*}
d_i+d_I&=78
end{align*}
$$

We haveadded the $d_b$ from $d_i$ because Ingrid and Bharat are travelling in opposite direction and the distance between them is greater and greater after every instant.
Now we need to substitute the values of $d_b$ and $d_i$ into $d_i+d_b=78$

$$
Rightarrow
$$

$$
begin{align*}
14t+12t&=78\
26t&=78tag{divide each side by 26}\
t&=dfrac{78}{26}\
t&=3 text{ hours}
end{align*}
$$

Therefore, After 3 hours the distance between Bharat and Ingrid becomes 78 kilometers.

$textbf{(a)}$ $dfrac{7b}{6}$

$textbf{(b)}$ After 3 hours the distance between Bharat and Ingrid becomes 78 kilometers.

We need to put the solution point $(1,6)$ into each of the given equations and observe if this point satisfy the equations or not. It the equations hold true for the given solution point then we will say that it is the correct solution for the given set of equations.

$bullet$ Checking for $4x+3y=22$

$$
begin{align*}
4x+3y&=22\
4(1)+3(6)&=22\
4+18&=22\
22&=22tag{ true}
end{align*}
$$

$bullet$ Checking for $x-2y=0$

$$
begin{align*}
x-2y&=0\
1-2(6)&=0\
1-12&=0\
-11ne0
end{align*}
$$

The solution point $(1,6)$ is not valid for the equation $x-2y=0$ and hence this solution is not correct.

The solution point $(1,6)$ is not valid for the equation $x-2y=0$ and hence this solution is not correct.

Let $g$ represents the number of green marbles in the bag and $r$ represents the number of red marbles in the bag. Given that there is twice the number of green marble than that of red marbles. So we can write it as equation shown below.

$$
g=2r
$$

Now given that there are a total of 84 marbles in the bag.
$Rightarrow$
$$
g+r=84
$$

Now, we have two variables to solve and have 2 equations.

$$
begin{align}
g&=2r\
g+r&=84
end{align}
$$

We can substitute the $g=2r$ from the equation (1) into the equation (2).

$$
Rightarrow
$$

$$
begin{align*}
g+r&=84\
(2r)+r&=84\
3r&=84tag{divide each side by 3}\
dfrac{3r}{3}&=dfrac{84}{3}\
r&=28
end{align*}
$$

Now, we can put $r=28$ into the equation (1) , to solve for $g$

$$
begin{align*}
g&=2r\
g&=2(28)\
g&=56
end{align*}
$$

Therefore, there are the 56 green marbles and 28 red marbles in the bag.

Let $t$ equal the time he walked then the time he travelled by bus is $2t$ all in hours.

Given that his walking speed was 3 miles per hour and speed of bus was 15 miles per hour.

This situation can be represented using an equation as shown below.

$$
begin{align*}
3cdot t+15 cdot 2t&=66\
3t+30t&=66\
33t&=66\
t&=dfrac{66}{33}\
t&=2text{ hours}
end{align*}
$$

Therefore, the distance travelled by Carter via bus is $2cdot 2=4$ hours

$4$ hours

Let $t$ represents the number of touchdowns and $f$ represents the number of field goals. Given that the number of field goals was one more than twice the number of touchdowns. The equation for this situation is

$$
f=2t+1
$$

Now, it is also mentioned that players are given 7 points for each touchdown and 3 points for each field goal. The total 55 points were scored during the game. The equation for this situation is

$$
7t+3f=55
$$

So, we have our system of the equation as

$$
begin{align}
f&=2t+1\
7t&+3f=55
end{align}
$$

$textbf{(a)}$ Option (b) correctly represents the given situation.

$textbf{(b)}$ We can substitute the value of $f$ from the equation (1) into the equation (2), this will result in the equation in terms of a single variable $(t)$ which can be solved easily as shown below.

$$
begin{align*}
7t&+3f=55\
7t&+3(2t+1)=55\
7t+6t+3&=55tag{subtarct 3 from the each side}\
13t&=55-3\
13t&=52tag{divide each side by 13}\
t&=4
end{align*}
$$

Now, put $t=4$ into the equation (1) and solve for $f$

$$
begin{align*}
f&=2t+1\
f&=2(4)+1\
f&=8+1\
f&=9
end{align*}
$$

Therefore, there were 4 touchdowns and 9 field goals during last night’s game.

$textbf{(a)}$ Option (b) correctly represents the given situation.

$textbf{(b)}$ There were 4 touchdowns and 9 field goals during last night’s game.

We have only two data points as information. $(-3,3)$ from the graph and $(-2,1)$ from the table. We can easily draw the graph of the line by locating these data points on the graph and then drawing a straight line through them. We can also, find the missing value of $y$ in the table with the help of the graph.\
The graph and the table is attached below.\
textbf{(a)} begin{center}begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
-3&3\
hline
-2&1\
hline
-1&-1\
hline
0&-3\
hline
1&-5\
hline
2&-7\
hline
3&-9\
hline
end{tabular}
end{center}

$textbf{(b)}$ We can check the more than one solution point from the table into the given line $2x+y=-3$. If these points satisfy the given equation then it is the correct representation otherwise we need to find the equation of the line on our own.

$bullet$ Checking for point $(-3,3)$

$$
begin{align*}
2x+y&=-3\
2(-3)+3&=-3\
-6+3&=-3\
-3&=-3tag{true}
end{align*}
$$

$bullet$ Checking for the point $(-2,1)$

$$
begin{align*}
2x+y&=-3\
2(-2)+1&=-3\
-4+1&=-3\
-3&=-3tag{true}
end{align*}
$$

The given equation $2x+y=-3$ holds true for the solution points from the table and graph, hence is it the correct representation.

$textbf{(a)}$ We have only two data points as information. $(-3,3)$ from the graph and $(-2,1)$ from the table. We can easily draw the graph of the line by locating these data points on the graph and then drawing a straight line through them. We can also, find the missing value of $y$ in the table with the help of the graph.

$textbf{(b)}$ Yes, $2x+y=-3$ is the correct equation for the given situation.

$textbf{(a)}$ Given sequence is an Geometric sequence with $a_1=2$ and common ratio $r=5$,
Because each term can be represented as $a_1cdot r^{n-1}$

$textbf{(b)}$ Shape of the graph is exponential as shown below.

$textbf{(c)}$
$$
begin{align*}
a_1&=2\
a_2&=a_1cdot 2=2cdot 5=2cdot 5^{2-1}=10\
a_3&=a_2cdot 5=10cdot 5=2cdot 5^{3-1}=50\
a_4&=a_3cdot 5=50cdot 5=2cdot 5^{4-1}=250\
a_n&=a_{n-1}cdot 5=2cdot 5^{n-1}\
end{align*}
$$

Therefore, explicit equation for the given sequence is $a_n=2cdot 5^{n-1}$

$textbf{(a)}$ Given sequence is an Geometric sequence with $a_1=2$ and common ratio $r=5$,
Because each term can be represented as $a_1cdot r^{n-1}$

$textbf{(b)}$ Exponential shape

$textbf{(c)}$ $a_n=2cdot 5^{n-1}$

Katy is correct, substitution method should give a new equation like $3x+2(6x-1)=43$.

This is because we are substituting the value of variable $y$ into the equation (2) where as Kevin is doing it wrong while substituting the value of variable $y$ into $x$ in the equation (2)

Katy is correct, substitution method should give a new equation like $3x+2(6x-1)=43$.

$$
textbf{(a)}
$$

$$
begin{align*}
&5^0cdot 2^{-3}\
&=dfrac{5^0}{2^{3}}\
text{On simplification, we get}\
&=dfrac{1}{2^{3}}
end{align*}
$$

$$
textbf{(b)}
$$

$$
begin{align*}
&dfrac{a^3}{b^{-2} }cdot dfrac{ab^2}{a^4}\
&=a^3 b^2 cdot dfrac{ab^2}{a^4}\
text{On simplification, we get}\
&=b^4\
end{align*}
$$

$textbf{(c)}$ $2.3times 10^{-3} cdot 4.2 times 10^2$

$$
begin{align*}
&2.3times 10^{-3} cdot 4.2 times 10^2\
&=(2.3cdot 4.2)times 10^{-3+2}\
&=9.66times 10^{-1}
end{align*}
$$

$textbf{(d)}$ $(3.5times 10^3)^2$

$$
begin{align*}
&(3.5times 10^3)^2\
&=(3.5^2)times (10^3)^2\
&=12.25times 10^6\
&=1.225times 10^7
end{align*}
$$

$textbf{(a)}$ $dfrac{1}{2^{3}}$

$textbf{(b)}$ $b^4$

$textbf{(c)}$ $9.66times 10^{-1}$

$textbf{(d)}$ $1.225times 10^7$

$textbf{(a)}$ $f(6w)$ indicates to “calculate the output for the input that is 6 times $x$.”

$textbf{(b)}$ $g(h-2)$ indicates to “calculate the output for the input that is 2 lesser than $h$.”

$textbf{(c)}$ $4j(a)+ 10$ indicates to “calculate the output for the input $a$ which is 10 greater than the 4 times of output of the input $a$.”

Let $x$ represents the number of xylophones and $y$ represents the number of yodelers on the gondola.It is given that the number of yodelers on the gondola is twice the number of xylophones. So we can write the equation as
$$
y=2x
$$

Now, Given that the gondola conductor charges $2 for each yodeler and $1 for each xylophone. The cost for the entire club is $40. So the equation for this situation becomes

$$
2y+x=40
$$

$bullet$ We have our system of the equations as

$$
begin{align}
y&=2x\
2y+x&=40
end{align}
$$

$bullet$ we can substitute the $y=2x$ using the equation (1) into the equation (2).

$$
Rightarrow
$$

$$
begin{align*}
2y+x&=40\
2(2x)+x&=40\
5x&=40tag{divide each side by 5}\
x&=8
end{align*}
$$

We can now put $x=8$ into the equation (1) to solve for $y$.

$$
Rightarrow
$$

$$
begin{align*}
y&=2x\
y&=2(8)\
y&=16
end{align*}
$$

Therefore, the number of yodelers on the gondola are 16 which is double of the number of xylophones (8) on the music trip.

For drawing graph of any line, we need to find at least two pair of $x$ and $y$ coordinates on this line. For this, we need to assume any one of the coordinate( Let’s say $x$) first and solve for the other coordinate ($y$)by putting the assumed coordinate into the given equation.

$bullet$ For $y=2x$

Let $x=0$

$$
begin{align*}
y&=2x\
y&=2(0)\
y&=0
end{align*}
$$

Therefore, the point is $(0,0)$

Now, for another point on this line, Let $x=1$

$$
begin{align*}
y&=2x\
y&=2(1)\
y&=2
end{align*}
$$

Therefore, the 2 points on the line $y=2x$ are $(0,0)$ and $(1,2)$. We can locate these points on the graph and we can easily draw a stright line through them.

$bullet$ For $2y+x=40$

Let $x=0$

$$
begin{align*}
2y+0&=40\
2y&=40\
y&=20
end{align*}
$$

Therefore, the point is $(0,20)$

Now, for another point on this line, Let $x=10$

$$
begin{align*}
2y+10&=40\
2y&=30\
y&=15
end{align*}
$$

Therefore, the 2 points on the line $2y+x=40$ are $(0,20)$ and $(10,15)$. We can locate these points on the graph and we can easily draw a straight line through them.

The graph of the lines is drawn with the help of the points obtained above. Some extra points are marked on the graph to fill the required table. The points in the table can be easily obtained using the coordinates of the graph corresponding to each line.
The tables for each of the line is included with the solution point shown in green colour.\
$bullet$ For $y=2x$
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
0&0\
hline
1&2\
hline
5&10\
hline
{color{green}{8}}&{color{green}{16}}\
hline
10&20\
hline
end{tabular}
end{center}
$bullet$ For $2y+x=40$
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
0&20\
hline
{color{green}{8}}&{color{green}{16}}\
hline
10&15\
hline
20&10\
hline
30&5\
hline
end{tabular}
end{center}

Discussion points
$bullet$ The solution to a two-variable equation can be the infinite number of values. It can be seen from the graph of the individual lines. Some solution points are marked on the graph attached above.

$bullet$ Individually each of the equations has an infinite number of solutions. These solutions are marked as points $(x,y)$ which lies on the graph of the lines (individually)

$bullet$ Solution point is the intersection point of both the lines.

$bullet$ The solution point is common in both the tables of individual lines.

$bullet$ We need to check the solution in both the equations because the solution point should satisfy both the cases and it is the intersection point of both the lines.

We have our system of the equations as

$$
begin{align}
y&=2x\
2y+x&=40
end{align}
$$

For drawing graph of any line, we need to find at least two pair of $x$ and $y$ coordinates on this line. For this, we need to assume any one of the coordinate( Let’s say $x$) first and solve for the other coordinate ($y$)by putting the assumed coordinate into the given equation.

The points in the table can be easily obtained using the coordinates of the graph corresponding to each line. For tables and the graph see inside.

textbf{(a)} Let $x$ represents the number of xylophones and $y$ represents the number of yodelers on the gondola.
Given that the gondola conductor charges $2 for each yodeler and $1 for each xylophone. The cost for the entire club is $40. So the equation for this situation becomes
$$2y+x=40$$
textbf{(b)} We can assume a value for one variable (let’s say $x$) first, then we can solve the value of the other $y$ by putting the value of $x$ into the equation.\
Let $x=20$ then $y$ corresponding to it will be
begin{align*}
2y+x&=40\
2y+20&=40\
2y&=20\
y&=10
end{align*}
Therefore, a combination of 5 xylophones and 10 yodelers satisfies the equation.\
No, there can be several other possible combinations for this equation.\\
textbf{(c)} We can find as many combinations as we need by using the method described in the part (b).\
The table for such combinations of $x$ and $y$ is made below.\
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
0&20\
hline
8&16\
hline
10&15\
hline
20&10\
hline
30&5\
hline
end{tabular}
end{center}

$textbf{(d)}$ According to Jon, there could be 6 xylophones and 12 yodelers on the gondola. This means the combination is $(6,12)$. We can put this combination into the equation to check its validity.

$$
begin{align*}
2y+x&=40\
2(12)+6&=40\
24+6&=40\
30ne40 tag{not valid}
end{align*}
$$

We can see that $(6,12)$ is not satisfying the equation and hence it is not a correct combination.

$textbf{(e)}$ Yes, Helga is right when she says that “Each correct combination is a solution to our equation”.

The solution to a two-variable equation is a point in terms of the variables arranged in a manner such that they make a coordinate (for example $(x,y)$ for the equation $2y+x=40$ ) and which on putting into the equation makes the equation true.

$textbf{(a)}$ $2y+x=40$

$textbf{(b)}$ $(20,10)$, No there can be several other possible combinations.

$textbf{(c)}$ See the table attached inside.

$textbf{(d)}$ No, Jon is incorrect.

$textbf{(e)}$ Yes, Helga is right.

textbf{(a)} Let $x$ represents the number of xylophones and $y$ represents the number of yodelers on the gondola. It is given that the number of yodelers on the gondola is twice the number of xylophones. So we can write the equation as $$y=2x$$
textbf{(b)} We can assume a value for one variable (let’s say $x$) first, then we can solve the value of the other $y$ by putting the value of $x$ into the equation.\
Let $x=10$ then $y$ corresponding to it will be
begin{align*}
y&=2x\
y&=2(10)\
y&=20
end{align*}
Therefore , a combination satisfying the equation $y=2x$ is $(10,20)$. We can similarly find the many other combinations as we require. The table for five such combinations is made below.\
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
0&0\
hline
1&2\
hline
5&10\
hline
8&16\
hline
10&20\
hline
end{tabular}
end{center}

$textbf{(c)}$ We have our system of the equations as

$$
begin{align}
y&=2x\
2y+x&=40
end{align}
$$

Now, we can substitute the $y=2x$ using the equation (1) into the equation (2).

$$
Rightarrow
$$

$$
begin{align*}
2y+x&=40\
2(2x)+x&=40\
5x&=40tag{divide each side by 5}\
x&=8
end{align*}
$$

We can now put $x=8$ into the equation (1) to solve for $y$.

$$
Rightarrow
$$

$$
begin{align*}
y&=2x\
y&=2(8)\
y&=16
end{align*}
$$

Therefore, the number of yodelers on the gondola are 16 and the number of xylophones are 8.

$textbf{(d)}$ Yes, the solution $(8,16)$ is a solution to both the equations $2y+x=40$ and $y=2x$. This is why it is called the solution of the system of the equations as it satisfies both the equations and lies on the intersection point of the both the lines on the graph.
We can check the validity in both the equation by putting $(8,16)$ in the equations and see if it makes the equations true or not.

$textbf{(a)}$ $y=2x$

$textbf{(b)}$ We can assume a value for one variable (let’s say $x$) first, then we can solve the value of the other $y$ by putting the value of $x$ into the equation. See the table attached inside.

$textbf{(c)}$ $(8,16)$

$textbf{(d)}$ Yes, the solution $(8,16)$ is a solution to both the equations $2y+x=40$ and $y=2x$. This is why it is called the solution of the system of the equations as it satisfies both the equations and lies on the intersection point of the both the lines on the graph.

$textbf{(a)}$ We can choose the solution points from the table we obtained in the problem 6-68. Then we locate these points on the graph and can easily draw a straight line passing through these points which will represent the required graph of the line. The graph is attached below and the shape of the graph is a straight line.

$textbf{(b)}$ The each point on the graph of the line represents the solution to the equation because line passes through these lines which is equivalent with coordinates of these points satisfies the equation of the line.

$textbf{(c)}$ Just like the part (a), we can use the points obtained in the problem 6-69 to draw the graph of the line.

$textbf{(d)}$ The coordinates of the point of intersection are $(8,16)$. The special about this point is that it lies on both the lines and hence it is a solution which satisfies both the equations of the line.

$textbf{(e)}$ The solution can be represented using equations, tables, and the graphs.

$textbf{(a)}$ Shape of the graph is a straight line.

$textbf{(b)}$ The each point on the graph of the line represents the solution to the equation because line passes through these lines which is equivalent with coordinates of these points satisfies the equation of the line.

$textbf{(c)}$ See the attached graph inside.

$textbf{(d)}$ $(8,16)$

$textbf{(e)}$ Using equations, tables, and the graphs

$y$-intercept of a line is where the line cuts the $y$- axis. So we can find the $y$-intercept of the line by putting $x=0$ in the equation of the line.

Similarly, $x$-intercept of a line is where the line cuts the $x$- axis. So we can find the $x$-intercept of the line by putting $y=0$ in the equation of the line.

$textbf{(a)}$ The equation for the cost is $2y+x=40$

$$
Rightarrow
$$

$bullet$ Finding $y$-intercept by putting $x=0$

$$
begin{align*}
2y+x&=40\
2y+(0)&=40\
2y&=40\
y&=20
end{align*}
$$

Therefore, $y$-intercept is 20.

$bullet$ Finding $x$-intercept by putting $y=0$

$$
begin{align*}
2y+x&=40\
2(0)+x&=40\
x&=40
end{align*}
$$

Therefore, $x$-intercept is 40.

$textbf{(b)}$ The equation is $y=2x$

$$
Rightarrow
$$

$bullet$ Finding $y$-intercept by putting $x=0$

$$
begin{align*}
y&=2x\
y&=2(0)\
y&=0
end{align*}
$$

Therefore, $y$-intercept is 0.

$bullet$ Finding $x$-intercept by putting $y=0$

$$
begin{align*}
y&=2x\
(0)&=2x\
dfrac{0}{2}&=x\
x&=0
end{align*}
$$

Therefore, $x$-intercept is 0.

$textbf{(c)}$ The graph intersect each other at $(8,16)$.

$textbf{(d)}$ The words intersection means the point where both the lines meet on the graph. This point satisfies both the equations. Whereas the word intercept is defined for individual lines. The intercept represents the distance from the origin to the point where a line cuts the axis. For example $y$-intercept is the point on the $y$ axis where the line cuts it.

$textbf{(a)}$ $y$-intercept is 20 and $x$-intercept is 40.

$textbf{(b)}$ $y$-intercept is 0 and $x$-intercept is 0.

$textbf{(c)}$ $(8,16)$

$textbf{(d)}$ The words intersection means the point where both the lines meet on the graph. This point satisfies both the equations. Whereas the word intercept is defined for individual lines. The intercept represents the distance from the origin to the point where a line cuts the axis. For example $y$-intercept is the point on the $y$ axis where the line cuts it.

Intercept is a special type of intersection. When a line intersects any of the axes then it is called intercept. For example when a line intersects the $y$ axis at any point then it is called its $y$-intercept.

Another way to define the $y$-intercept is that it is the value of the variable $y$ where $x$ becomes 0. Similarly the $x$-intercept is the value of $x$ corresponding to $y=0$.

$textbf{(a)}$ The graphical solution will be represented by the intercept.

$textbf{(b)}$ The graphical solution will be best represented by the intersection of both the lines.

$textbf{(c)}$ The graphical solution will be represented by the intercepts of the individual lines

$textbf{(a)}$ Intercept

$textbf{(b)}$ Intersection

$textbf{(c)}$ By individual intercepts

Point $(3.687,6.256)$ will satisfy the both the function. This is because, this point is the intersection point of both the lines on the graph. For estimating this point from the graph we need a better scaled graph like shown above.\
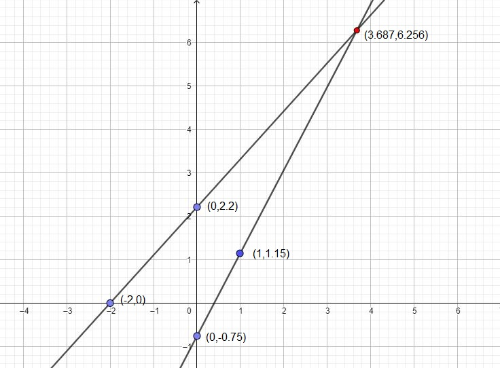
Now, confirming the point of intersection from the tables.\\
$f(x) = 1.1x+ 2.2$\
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
-2&0\
hline
0&2.2\
hline
1&3.3\
hline
3.687&6.256\
hline
end{tabular}\\\
$g(x) = 1.9x – 0.75$\
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
-2&-4.55\
hline
0&-0.75\
hline
1&1.15\
hline
3.687&6.256\
hline
end{tabular}\\
From the table of values for each equation, we can verify the result.\

Point $(3.687,6.256)$ will satisfy the both the function.

Graph and tables are drawn in the solution.

$textbf{(a)}$ Let h represent the number of hotdogs and c represent the number of corndogs.

Given that the number of hotdogs sold was three fewer than twice the number of corndogs sold. This situation can be represented using equation as shown below.

$$
2c-h=3
$$

$textbf{(b)}$ Given that a hotdog costs $3 and a corndog costs $1.50 and the total collection was $201. Now, this can be represented as equation as

$$
3h+1.5c=201
$$

$textbf{(c)}$ For solving the given equation, we can use Substitution method. We multiply each side of the equation $2c-h=3$ with 3 and then add it into the second equation as shown below.

$$
begin{align*}
3(2c-h)&=3cdot 3\
6c-3h&=9
end{align*}
$$

Now, adding $6c-3h=9$ to respective sides of $3h+1.5c=201$

$$
begin{align*}
3h+1.5c+(6c-3h)&=201+(9)\
7.5c&=210\
c&=dfrac{210}{7.5}\
c&=28\
end{align*}
$$

Therefore, the number of corndog sold were 28.

$textbf{(a)}$ $2c-h=3$

$textbf{(b)}$ $3h+1.5c=201$

$textbf{(c)}$ 28

If $a=b$ and $c=d$ the we replace the variables accordingly in the given equation $a+c=b+d$ like shown below.

$$
begin{align*}
a+c&=b+dtag{replace $a$ by $b$ and $c$ by $d$ in LHS }\
(b)+(d)&=b+d\
b+d&=b+dtag{true}
end{align*}
$$

Therefore, Rianna is correct.

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
-left(2-3xright)+x=9-x& {;}quad : -2+4x=9-xtag{Expand}\
&-2+4x+2=9-x+2tag{Add 2 to both sides} \
&4x=-x+11tag{Simplify} \
&4x+x=-x+11+xtag{Add x to both sides } \
&5x=11tag{Simplify} \
&frac{5x}{5}=frac{11}{5}tag{Divide both sides by 5} \
&{color{#c34632}x=frac{11}{5}}
end{align*}
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
frac{6}{x+2}=frac{3}{4}& {;}quad : 6cdot :4=left(x+2right)cdot :3tag{Multiply }\
&left(x+2right)cdot :3=6cdot :4tag{Switch sides} \
&left(x+2right)cdot :3=24tag{Multiply the numbers} \
&frac{left(x+2right)cdot :3}{3}=frac{24}{3}tag{Divide both sides by 3 } \
&x+2=8tag{Simplify} \
&x+2-2=8-2tag{Subtract 2 from both sides} \
&{color{#c34632}x=6}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Apply:fraction:cross:multiply::if:}frac{a}{b}=frac{c}{d}mathrm{:then:}acdot :d=bcdot :c
$$

$$
text{ }
$$

$$
text{ }
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
5-2left(x+6right)=14& {;}quad : 5-2left(x+6right)-5=14-5tag{Subtract 5 from both sides}\
&-2left(x+6right)=9tag{Simplify} \
&frac{-2left(x+6right)}{-2}=frac{9}{-2}tag{Divide both sides by -2 } \
&x+6=-frac{9}{2}tag{Simplify} \
&x+6-6=-frac{9}{2}-6tag{Subtract 6 from both sides} \
&-frac{9}{2}-6=-frac{6}{1}-frac{9}{2}=-frac{6cdot :2}{2}-frac{9}{2}=frac{-2cdot :6-9}{2}tag{Simplify} \
&{color{#c34632}x=-frac{21}{2}}
end{align*}
$$

$$
{color{#4257b2}text{d)}}
$$

$$
begin{align*}
frac{1}{2}x-4+1=-3-frac{1}{2}x& {;}quad : frac{1}{2}x-3=-3-frac{1}{2}xtag{Add/Subtract the numbers }\
&frac{1}{2}x-3+3=-3-frac{1}{2}x+3tag{Add 3 to both sides} \
&frac{1}{2}x=-frac{1}{2}xtag{Simplify} \
&frac{1}{2}x+frac{1}{2}x=-frac{1}{2}x+frac{1}{2}xtag{Add 1/2x to both sides } \
&{color{#c34632}x=0}
end{align*}
$$

$$
color{#4257b2}text{ a) } x=frac{11}{5}
$$

$$
color{#4257b2}text{ b) }x=6
$$

$$
color{#4257b2}text{ c) }x=-frac{21}{2}
$$

$$
color{#4257b2} text{ d) }x=0
$$

Let $a_n$ represents the $n^text{th}$ term of the sequence. Then we can find the given terms of the sequence form the graph.

$$
begin{align*}
a_2&=8\
a_3&=4\
a_4&=2
end{align*}
$$

We can see that each next term of the given sequence can be obtained by multiplying the previous term by $dfrac{1}{2}$. This kind of sequence is called a geometric sequence. The general term of a geometric sequence is given by
$$
a_n=a_1cdot (r)^{n-1}
$$

where $a_1$ is the first term of the sequence and $r$ represent the common ratio.

The common ratio is also called a sequence generator which can be found out by taking the ratio of any 2 consecutive terms such that $r=dfrac{a_n}{a_{n-1}}$
The $r$ in our case is $r=dfrac{a_3}{a_2}=dfrac{4}{8}=dfrac{1}{2}$
Similarly we can find our first term $a_1$

$$
r=dfrac{a_2}{a_1}=dfrac{1}{2}
$$

$$
Rightarrow
$$

$$
begin{align*}
dfrac{8}{a_1}&=dfrac{1}{2}tag{multiply each side by $2a_1$}\
dfrac{8}{a_1} cdot (2a_1)&=dfrac{1}{2}cdot (2a_1)\
16&=a_1\
a_1&=16
end{align*}
$$

Now, we can put $a_1=16$ and $r=dfrac{1}{2}$ into the general equation.

$$
a_n=16cdot (dfrac{1}{2})^{n-1}
$$

Therefore, the explicit equation for the graphed sequence is
$$
boxed{a_n=16cdot (dfrac{1}{2})^{n-1}}
$$

$$
a_n=16cdot (dfrac{1}{2})^{n-1}
$$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
&text{Subtract 5 from both sides}\
&5-left(y-2right)-5=3x-5\\
&-left(y-2right)=3x-5 tag{Simplify} \
&frac{-left(y-2right)}{-1}=frac{3x}{-1}-frac{5}{-1} tag{Divide both sides by -1}\
&y-2=-3x+5 tag{Simplify}\
&y-2+2=-3x+5+2 tag{Add 2 to both sides}\\
&boxed{{color{#c34632} y=-3x+7 } }
end{align*}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
&text{Divide both sides by 5}\
&frac{5left(x+yright)}{5}=frac{-2}{5}\\
&x+y=-frac{2}{5} tag{Simplify} \
&x+y-x=-frac{2}{5}-x tag{Subtract x from both sides}\\
&boxed{{color{#c34632} y=-frac{2}{5}-x } }
end{align*}
$$

$$
color{#4257b2} text{a)}y=-3x+7
$$

$$
color{#4257b2} text{b)}y=-frac{2}{5}-x
$$

First, we need to rearrange the $2x+3y=-2$, this can be done by the way shown below.

$$
begin{align*}
2x+3y&=-2tag{subtract $2x$ from the each side}\
2x-2x+3y&=-2-2x\
3y&=-2-2xtag{divide each side by 3 }\
dfrac{3y}{3}&=dfrac{-2-2x}{3}\
y&=dfrac{-2-2x}{3}
end{align*}
$$

Now, we have our system of equation as

$$
begin{align*}
y&=dfrac{-2-2x}{3}\
5x-3y&=16
end{align*}
$$

Now we need to substitute the value of $y$ using the equation (1) into the equation (2)

$$
begin{align*}
5x-3y&=16\
5x-3(dfrac{-2-2x}{3})&=16\
5x-(-2-2x)&=16\
5x+2+2x&=16\
7x&=14tag{divide each side by 7}\
x&=2
end{align*}
$$

Now, put $x=2$ into the equation (1) and solve for $y$.

$$
begin{align*}
y&=dfrac{-2-2(2)}{3}\
y&=dfrac{-2-4}{3}\
y&=dfrac{-6}{3}\
y&=-2
end{align*}
$$

Therefore, the solution for the given set of equation is $(2,-2)$

The solution for the given set of equations is $(2,-2)$.

$textbf{(a)}$ $2x+3y=-2$

$textbf{(b)}$
$$
begin{align*}
2x+3y&=-2\
+(5x-3y) & text{ } +16\
7x&=14
end{align*}
$$

By doing this, $y$-terms get cancelled and we have only equation in terms of only $x$ as variable.
Now, solving the obtained equation in single variable.

$$
begin{align*}
x&=dfrac{14}{7}\
x&=2
end{align*}
$$

$textbf{(c)}$ Using $x=2$, solving for y, in the equation $2x+3y=-2$

$$
begin{align*}
2cdot 2 +3y&=-2\
4+3y&=-2\
3y&=-6\
y&=dfrac{-6}{3}\
y&=-2
end{align*}
$$

As now we have solution point $(x,y)=(2,-2)$, checking the validity for this solution in the original equations.

Putting $(x,y)=(2,-2)$ into $2x+3y=-2$, we get

$$
begin{align*}
2cdot 2 +3cdot -2&=-2\
4-6&=-2\
-2&=-2
end{align*}
$$

Hence, it satisfies the equation $2x+3y=-2$

Now, $(x,y)=(2,-2)$ into $5x-3y=16$, we get

$$
begin{align*}
5cdot 2 -3cdot -2 &=16\
10+6&=16\
16&=16
end{align*}
$$

Hence, it satisfy equation $5x-3y=16$ also. Therefore our new method as well as solution is correct.

$textbf{(d)}$ Given pair of equation are

$$
begin{align}
2x-y&=-2\
-2x+3y&=10
end{align}
$$

Like done in the above example, we can add +10 to the each side, and because from the equation (2), we have $10=-2x+3y$, then we can add $-2x+3y$ on the left side of equation (1) and +10 on the right side of equation (1). which gives,

$$
begin{align*}
2y&=8\
y&=dfrac{8}{2}\
y&=4end{align*}
$$

Now, putting $y=4$ into the equation $2x-y=-2$, we can solve for $x$

$$
begin{align*}
2x-4&=-2\
2x&=-2+4\
2x&=2\
x&=dfrac{2}{2}\
x&=1
end{align*}
$$

As now we have solution point $(x,y)=(1,4)$, checking the validity for this solution in the original equations.

Putting $(x,y)=(1,4)$ into $2x-y=-2$, we get

$$
begin{align*}
2cdot 1 -1cdot 4&=-2\
2-4&=-2\
-2&=-2
end{align*}
$$

Hence, $(x,y)=(1,4)$ satisfies the equation $2x-y=-2$

Therefore we have a verified answer.

$textbf{(a)}$ $2x+3y=-2$

$textbf{(b)}$ $x=2$

$textbf{(c )}$ $y=-2$

$textbf{(d)}$ $(x,y)=(1,4)$

Let $x$ represents the number of basses and $y$ represents the number of trouts caught by Pat.
It is given that Each bass weighed three pounds, and each trout weighed one pound. Pat caught a total of 30 pounds of fish. So we can write the equation for this case as shown below.

$$
3cdot x+1cdot y=30
$$

Now, Given that, He got five points in the competition for each bass, and he lost one point for each trout. Pat scored a total of 42 points. So the equation for this case is
$$
5cdot x-1cdot y=42
$$

$textbf{(a)}$ The system of equations for the given information is

$$
begin{align}
3x+y&=30\
5x-y&=42
end{align}
$$

$textbf{(b)}$ This system is a good candidate for the elimination method because when adding the left-hand side of both the equations, the variable $y$ get canceled and hence we can easily solve for the $x$ in the resulting single variable equation.

$textbf{(c)}$ From the equation (2) we have $5x-y$ equal to 42. so we add $5x-y$ to the left-hand side and $42$ to the right-hand side of the equation (1).

$$
begin{align*}
3x+y&=30\
+(5x-y) & +(42)\
3x+5x+y-y&=30+42\
8x&=72tag{divide each side by 8}\
dfrac{8x}{8}&=dfrac{72}{8}\
x&=9
end{align*}
$$

Put $x=9$ into the equation (1) and solve for $y$.

$$
begin{align*}
3x+y&=30\
3(9)+y&=30\
27+y&=30tag{subtract 27 from the each side}\
27-27+y&=30-27\
y&=3
end{align*}
$$

We can check our solution by putting the solution point $(9,3)$ into both the equations one by one.

$bullet$ checking our solution in $3x+y=30$

$$
begin{align*}
3x+y&=30\
3(9)+(3)&=30\
27+3&=30\
30&=30tag{true}
end{align*}
$$

$bullet$ checking our solution in $5x-y=42$

$$
begin{align*}
5x-y&=42\
5(9)-(3)&=42\
45-3&=42\
42&=42tag{true}
end{align*}
$$

We can see that our solution point is valid for both the equations. Hence we can say that, Pat caught 9 basses and 3 trouts during the fishing competition.

$textbf{(a)}$ The system of equations for the given information is

$$
begin{align*}
3x+y&=30\
5x-y&=42
end{align*}
$$

$textbf{(b)}$ This system is a good candidate for the elimination method because when adding the left-hand side of both the equations, the variable $y$ get canceled and hence we can easily solve for the $x$ in the resulting single variable equation.

$textbf{(c)}$ Pat caught 9 basses and 3 trouts during the fishing competition.

We can multiply each term of the second equation by $-1$. This transformation will not affect the solution point as both sides of the equation is undergoing the same operation. After this, we can add the same value on both the side of the first equation by using the transformed second equation. in this way, the term of $x$ will get eliminated.

We have the system of equations as

$$
begin{align}
2x+7y&=13\
2x+3y&=5
end{align}
$$

Multiply each term of the equation (2) by $-1$. So the equation becomes

$$
begin{align*}
-2x-3y&=-5
end{align*}
$$

Now we can add $-5$ to each side of the equation (1). From the transformed equation we have $-5$ equal to $-2x-3y$ so we can add $-2x-3y$ to the left-hand side and $-5$ to the right-hand side.

$$
begin{align*}
2x+7y&=13\
(-2x-3y)& (-5)\
2x-2x+7y-3y&=13-5\
4y&=8tag{divide each side by 4}\
dfrac{4y}{4}&=dfrac{8}{4}\
y&=2
end{align*}
$$

Put $y=2$ into the equation (1) and solve for $x$.

$$
begin{align*}
2x+7y&=13\
2x+7(2)&=13\
2x+14&=13tag{subtract 14 from the each side}\
2x+14-14&=13-14\
2x&=-1tag{divide each side by 2}\
dfrac{2x}{2}&=dfrac{-1}{2}\
x&=dfrac{-1}{2}
end{align*}
$$

So the solution point is $(-dfrac{1}{2},2)$

We can check our solution by putting the solution point $(-dfrac{1}{2},2)$ into both the equations one by one.

$bullet$ checking our solution in $2x+7y=13$

$$
begin{align*}
2x+7y&=13\
2(-dfrac{1}{2})+7(2)&=13\
-1+14&=13\
13&=13tag{true}
end{align*}
$$

$bullet$ checking our solution in $2x+3y=5$

$$
begin{align*}
2x+3y&=5\
2(-dfrac{1}{2})+3(2)&=5\
-1+6&=5\
5&=5tag{true}
end{align*}
$$

The solution point $(-dfrac{1}{2},2)$ satisfies both the equations hence we can say that our solution is valid.

The solution point for the given system of equations is $(-dfrac{1}{2},2)$.

$textbf{(a)}$ Given pair of lines are

$$
begin{align}
2y-x&=5\
-3y+x&=-9
end{align}
$$

For solving above pair of lines by elimination method, we need to add -9 to the each side of equation (1). Now, as we have $-9=-3y+x$ form the equation (2), hence we can add $-3y+x$ in the left side of equation (1) and add -9 on the right side of equation (1). which is shown below,

$$
begin{align*}
2y-x&=5\
+(-3y+x)&text { } text { }text { }+(-9)\
-y&=-4\
y&=4
end{align*}
$$

We can use the value $y=4$ into any of the equation to solve for the value of $x$, here lets put $y=4$ in $-3y+x=-9$

$$
begin{align*}
-3cdot 4 +x&=-9\
-12+x&=-9\
x&=-9+12\
x&=3
end{align*}
$$

Now, we have solution point as $(3,4)$ , which can be checked by putting it any given line to see it satisfies the equation or not.

Lets put $(3,4)$ into $-3y+x=-9$ , we see that

$$
begin{align*}
(-3cdot 4+ 3)&=-9\
-12+3&=-9\
-9&=-9
end{align*}
$$

We can see that the solution point is satisfying the equation, hence the result is verified.Similarly, we can verify it by putting in other equation also.

$textbf{(b)}$ Given pair of lines are

$$
begin{align}
2x-4y&=14\
4y-x&=-3
end{align}
$$

For solving above pair of lines by elimination method, we need to add -3 to the each side of equation (1). Now, as we have $-3=4y-x$ form the equation (2), hence we can add $4y-x$ in the left side of equation (1) and add -3 on the right side of equation (1). which is as shown below,

$$
begin{align*}
2x-4y&=14\
+(4y-x)&text { } text { }text { }+(-3)\
x&=11\
end{align*}
$$

We can use the value $x=11$ into any of the equation to solve for the value of $y$, here lets put $x=11$ in $4y-x=-3$

$$
begin{align*}
4y-11&=-3\
4y&=-3+11\
4y&=8\
y&=dfrac{8}{4}\
y&=2
end{align*}
$$

Now, we have solution point as $(11,2)$ , which can be checked by putting it any given line to see it satisfies the equation or not.

Lets put $(11,2)$ into $2x-4y=14$ , we see that

$$
begin{align*}
(2cdot 11-4cdot 2)&=14\
22-8&=14\
14&=14
end{align*}
$$

We can see that the solution point is satisfying the equation, hence the result is verified.Similarly, we can verify it by putting in other equation also.

$textbf{(c)}$ Given pair of lines are

$$
begin{align}
3x+4y&=1\
2x+4y&=2
end{align}
$$

For solving above pair of lines by elimination method, we need to subtract $2$ from the each side of equation (1). Now, as we have $2=2x+4y$ form the equation (2), hence we can subtract $2x+4y$ from the left side of equation (1) and subtract 2 from the right side of equation (1). which is as shown below,

$$
begin{align*}
3x+4y&=1\
-(2x+4y)&text { } text { }text { }-(2)\
x&=-1\
end{align*}
$$

We can use the value $x=-1$ into any of the equation to solve for the value of $y$, here lets put $x=-1$ in $2x+4y=2$

$$
begin{align*}
2cdot -1+4y&=2\
-2+4y&=2\
4y&=2+2\
y&=dfrac{4}{4}\
y&=1
end{align*}
$$

Now, we have solution point as $(-1,1)$ , which can be checked by putting it any given line to see it satisfies the equation or not.

Lets put $(-1,1)$ into $3x+4y=1$ , we see that

$$
begin{align*}
(3cdot -1+4cdot 1)&=1\
-3+4&=1\
1&=1
end{align*}
$$

We can see that the solution point is satisfying the equation, hence the result is verified.Similarly, we can verify it by putting in other equation also.

$textbf{(d)}$ The graph of each pair of lines will intersect at their solution points which we obtained into the respective parts.

$textbf{(a)}$ $(3,4)$

$textbf{(b)}$ $(11,2)$

$textbf{(c)}$ $(-1,1)$

$textbf{(d)}$ The graph of each pair of lines will intersect at their solution points which we obtained into the respective parts.

$textbf{(a)}$ Given pair of lines are

$$
begin{align}
y&=-x+8\
y&=x-2
end{align}
$$

For solving above pair of lines we can use elimination method, we need to add y to the each side of equation (1). Now, as we have $y=x-2$ form the equation (2), hence we can add $y$ in the left side of equation (1) and add $x-2$ on the right side of equation (1). which is shown below,

$$
begin{align*}
y&=-x+8\
+(y)&text { } text { }text { }+(x-2)\
y+y&=-x+x+8-2\
2y&=6\
y&=dfrac{6}{2}\
y&=3
end{align*}
$$

We can use the value $y=3$ into any of the equation to solve for the value of $x$, here lets put $y=3$ in $y=x-2$

$$
begin{align*}
3&=x-2\
x&=3+2\
x&=5
end{align*}
$$

Hence, we have solution point as $(5,3)$

$textbf{(b)}$ Given pair of lines are

$$
begin{align}
2x-y&=10\
y=-4x&+2
end{align}
$$

we can write equation (4) as $4x+y=2$ by rearranging. Now, we can solve it just like part (a) using elimination method

For solving above pair of lines we can use elimination method, we need to add 2 to the each side of equation (1). Now, as we have $2=4x+y$ form the latest equation, hence we can add $4x+y$ in the left side of equation (1) and add $2$ on the right side of equation (1). which is shown below,

$$
begin{align*}
2x-y&=10\
+(4x+y)&text { } text { }text { }+(2)\
6x&=12\
x&=dfrac{12}{6}\
x&=2
end{align*}
$$

We can use the value $x=2$ into any of the equation to solve for the value of $y$, here lets put $x=2$ in $2x-y=10$

$$
begin{align*}
2cdot 2-y&=10\
4-y&=10\
-y&=10-4\
-y&=6\
y&=-6
end{align*}
$$

Hence, we have solution point as $(2,-6)$

$textbf{(a)}$ $(5,3)$

$textbf{(b)}$ $(2,-6)$

The given system of equation is

$$
begin{align}
y&=-2x+5\
2y&+4x=10
end{align}
$$

We can solve this system using the substitution method. Substitute the value of $y$ from the equation (1) into the equation (2).

$$
begin{align*}
2y+4x&=10\
2(-2x+5)+4x&=10tag{simplify}\
-4x+10+4x&=10\
10&=10tag{true always}
end{align*}
$$

The given system of equation is true always, irrespective to the value of $x$. Therefore, this system has an infinite number of solutions together.

$textbf{(b)}$ Both the lines overlap with each other.

$textbf{(c)}$ Yes, The graph in part (b) explains the result in part (a). As the lines overlap with each other. The any point satisfying the line with equation $y=-2x+5$ will also satisfy $2y+4x=10$ hence these will have the infinite number of solutions together.

$textbf{(a)}$ The given system of equation is true always, irrespective to the value of $x$. Therefore, this system has an infinite number of solutions together.

$textbf{(b)}$ Both the lines overlap with each other.

$textbf{(c)}$ Yes, The graph in part (b) explains the result in part (a). As the lines overlap with each other. The any point satisfying the line with equation $y=-2x+5$ will also satisfy $2y+4x=10$ hence these will have the infinite number of solutions together.

$textbf{(a)}$ Let the $x$ is the number of pizza slices sold in cafetaria and $y$ is number of burritos sold on Tuesday.
Given that the number of pizza slices sold was 20 less than the twice of the number of burritos sold.

We can represent the following condition by an equation as shown below.

$$
2y-20=x
$$

Now, given that the cost of a pizza slice is $2.50 and cost of a burritos is $3.00 and the total income collected by the cafetaria is $358 for selling these two items. This can be represented into the form of equation as shown below

$$
2.5x+3y=358
$$

Hence, we have our two equations as
$$
begin{align}
2y-x&=20\
2.5x+3y&=358
end{align}
$$

$textbf{(b)}$ for solving the given equations, we have $x=2y-20$ by using the equation (1).On putting $x=2y-20$ into equation (2) we can get an equation in terms of variable $y$ only. On solving further we can obtain value of $y$ and then $x$.

$$
begin{align*}
2.5(2y-20) +3y&=358\
5y-50+3y &=358\
8y&=358+50\
8y&=408\
y&=dfrac{408}{8}\
y&=51
end{align*}
$$

Now, putting $y=51$ into $2y-x=20$, we can solve for $x$

$$
begin{align*}
2cdot 51 -x&=20\
102-x&=20\
x&=102-20\
x&=82
end{align*}
$$

Therefore, the number of pizza slices sold was 82 and number of burritos sold was 51.

$textbf{(a)}$ Given current cost of the item is $20 and price increase is 5% per year\$Rightarrow$price after one year$= 20 +20times $dfrac{5}{100}$=20times(1.05)
$$
\
Hence, the multiplier is 1.05\\
textbf{(b)} with the continued trend the cost in 5 years will be
begin{align*}
text{cost in 1 year}&= 20times 1.05\
text{cost in 2 year}&= (20times 1.05)times 1.05\
text{cost in 3 year}&= ((20times 1.05)times 1.05)times 1.05\
Rightarrow text{cost in n year}&= 20times (1.05)^n tag{text{on generalising}}\
text{cost in 5 year}&= 20times (1.05)^5\
text{cost in 5 year}&= $25.525
end{align*}\
textbf{(c)} As derived above, cost in n year
$$
= $20times (1.05)^n$
where, $1.05$ represents the multiplier per year including the 5% increase, and n represents the number of years.

$textbf{(a)}$ 1.05

$textbf{(b)}$ $25.525\
textbf{(c)}$ $20times (1.05)^n$

$textbf{(a)}$ Given that the train traveled 90 miles in 1.5 hours. we need to find the time taken by the train to travel 330 miles. Let the train takes $t$ hours to cover 330 miles. We can do this by using the proportions shown below.

$$
90:15::30:t
$$

$$
Rightarrow
$$

$$
begin{align*}
dfrac{90 text{ miles}}{1.5text{ hours}}&=dfrac{330text{ miles}}{t}\
60&=dfrac{330}{t}tag{multiply each side by $t$}\
60cdot t&=dfrac{330}{t} cdot t\
60t&=330tag{divide each side by 60}\
t&=dfrac{330}{60}\
t&=5.5 text{ hours}
end{align*}
$$

$textbf{(b)}$ We can find the speed of the train by using $d=rt$ where $d$ is the distance, $r$ is speed and $t$ is the time taken.

$$
begin{align*}
r&=dfrac{90}{1.5} (dfrac{text{ miles}}{text{hour}})\
r&=60 (dfrac{text{ miles}}{text{hour}})
end{align*}
$$

Now, to cover the distance 330 miles with the speed 60 $dfrac{text{ miles}}{text{hour}}$ we can find the times taken by using the same equation.

$$
begin{align*}
d&=rt\
(330)&=(60)t\
dfrac{330}{60}&=t\
t&=5.5 text{ hours}
end{align*}
$$

$textbf{(c)}$ Yes, we got the same solution using both the methods.

$textbf{(a)}$ $t=5.5 text{ hours}$

$textbf{(b)}$ $t=5.5 text{ hours}$

$textbf{(c)}$ Yes, we got the same solution using both the methods.

$textbf{(a)}$

$$
begin{align*}
&2^3cdot 5^{-2}tag{use $a^{-m}=dfrac{1}{a^m}$}\
&=dfrac{2^3}{5^2}\
&=dfrac{2cdot 2cdot 2}{5cdot 5}\
&=boxed{dfrac{8}{25}}
end{align*}
$$

$$
textbf{(b)}
$$

$$
begin{align*}
&(xy^2)^3cdot (x^{-2})tag{use $(ab)^m=a^mb^m$}\
&=x^3(y^2)^3cdot x^{-2}tag{use $(a^m)^n=a^{mcdot n}$}\
&=x^3y^6cdot x^{-2}tag{use $a^{-m}=dfrac{1}{a^m}$}\
&=x^3y^6cdot dfrac{1}{x^2}\
&=dfrac{x^3y^6}{x^2}\
&=left (dfrac{x^3}{x^2} right ) y^6\
&=boxed{xy^6}
end{align*}
$$

In simple words, we can say that a number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10.

In order to write any given number into the scientific notation, we need to follow some sets of rules.

The number should be written in such a way that there should be a decimal point immediately after the leftmost digit, which should be greater than 1 and less than 10. After this decimal point, the required number of digits are put and then multiplication by a power of 10 with the sign of multiplication as it is.
For example $2.566times 10^-9$ is written in scientific form.

$textbf{(c)}$
$$
begin{align*}
&3times 10^3cdot 4times 10^5tag{separating the power terms}\
&=(3cdot 4)times (10^3cdot 10^5)tag{use $a^mcdot a^n=a^{m+n}$}\
&=12times 10 ^{3+5}tag{convert into scientific form}\
&=1.2 times 10^{8+1}\
&=boxed{1.2times 10^9}
end{align*}
$$

$textbf{(d)}$

$$
begin{align*}
&dfrac{4times 10^2}{5times 10^{-2}}\
&=left ( dfrac{4}{5} right)times left ( dfrac{10^2}{10^{-2}} right)tag{use $dfrac{a^m}{a^n}=a^{m-n}$}\
&=0.8times 10^{2-(-2)}\
&=0.8times 10^4tag{convert in scientific form}\
&=(0.8times 10 )times 10^3\
&=8times 10^3\
&=boxed{8times 10^3}
end{align*}
$$

$textbf{(a)}$ $dfrac{8}{25}$

$textbf{(b)}$ $xy^6$

$textbf{(c)}$ $1.2times 10^9$

$textbf{(d)}$ $8times 10^3$

Let Phoebe’s mom bought $x$ dragonfly wings and $y$ fairy wings. It is given that total 11 friends were attending party.

$$
Rightarrow x+y=11 text{ } text { (1) }
$$

Now, cost for dragonfly wings is $1 and the cost for fairy wing is $2 . Phoebe’s mom spent total $18 on the gifts, then we can represent this into the equation as shown below

$$
1cdot x +2cdot y=18
$$

$$
Rightarrow x + 2y=18 text{ } text { (2) }
$$

Now, solving the equations for the values of $x$ and $y$

$$
begin{align*}
x+y&=11\
x=11&-y
end{align*}
$$

Now putting $x=11-y$ into eq (2), we get

$$
begin{align*}
(11-y)+2y &=18\
11+y&=18\
y&=7
end{align*}
$$

putting $y=7$ into $x+y=11$, we get

$$
begin{align*}
x+7&=11\
x&=11-7\
x&=4
end{align*}
$$

Hence, Phoebe’s mom bought 4 dragonfly wings and 7 fairy wings.

The given system of equations is

$$
begin{align*}
2x+y&=10\
3x-2y&=1
end{align*}
$$

$$
textbf{(a)}
$$

$$
begin{align*}
2x+y&=10\
+(3x-2y)& +(1)\
2x+y+3x-2y&=10+1\
5x-y&=11
end{align*}
$$

Therefore, on combining both the given equation we get $boxed{5x-y=11}$

$textbf{(b)}$ Yes, $2x+y=10$ is equivalent to $4x+2y=10$. We can get the second equation by multiplying the first equation by 2.
As both the equation is equivalent, hence their graph will also be the same.

$textbf{(c)}$ Yes, $4x+2y=20$ can be used instead of $2x+y=10$ to solve the system. We can replace the $2x+y=10$ with $4x+2y=20$ in the system of equations. So we have modified the system of equations as shown below.

$$
begin{align}
4x+2y&=20\
3x-2y&=1
end{align}
$$

We can use elimination method to solve this system. We can add both the equations to eleminate the $y$ fron the equation as shown below.

$$
begin{align*}
4x+2y&=20\
+(3x-2y)& +(1)\
4x+3x+2y-2y&=20+1\
7x&=21tag{divide each side by 7}\
dfrac{7x}{7}&=dfrac{21}{7}\
x&=3
end{align*}
$$

Now, put $x=3$ into the equation (2) to solve for $y$.

$$
begin{align*}
3x-2y&=1\
3(3)-2y&=1\
9-2y&=1tag{subtract $9$ from the each side}\
-2y&=1-9\
-2y&=-8tag{divide each side by -2}\
dfrac{-2y}{-2}&=dfrac{-8}{-2}\
y&=4
end{align*}
$$

The solution point is $(3,4)$

We can check our solution by putting $(3,4)$ into both the original equations one by one.

$bullet$ Checking for $2x+y=10$

$$
begin{align*}
2x+y&=10\
2(3)+(4)&=10\
6+4&=10\
10&=10tag{true}
end{align*}
$$

$bullet$ Checking for $3x-2y=1$

$$
begin{align*}
3x-2y&=1\
3(3)-2(4)&=1\
9-8&=1\
1&=1tag{true}
end{align*}
$$

We can see the the solution point $(3,4)$ is satisfying both the given equations. Henc eour solution is valid.

$textbf{(d)}$ The top equation was changed because after this transformation we can use the elimination method to solve this system as the variable $x$ gets eliminated on adding the equations after transformation.

No, the elimination method wouldn’t have worked if the bottom equation was multiplied by 2. On this transformation, no variable will get eliminated on adding the transformed equations.

The transformed system becomes

$$
begin{align*}
2x+y&=10\
6x-4y&=2
end{align*}
$$

Combining both the equation above, the resultant is

$$
begin{align*}
2x+y&=10\
+(6x-4y)& +(2)\
2x+6x+y-4y&10+2\
8x-3y&=12
end{align*}
$$

Therefore, we can see that not any variable is eliminated here. So the method of elimination will not work for this transformation.

$textbf{(a)}$ $5x-y=11$

$textbf{(b)}$ Yes, $2x+y=10$ is equivalent to $4x+2y=10$. We can get the second equation by multiplying the first equation by 2.
As both the equation is equivalent, hence their graph will also be the same.

$textbf{(c)}$ $(3,4)$

$textbf{(d)}$ The top equation was changed because after this transformation we can use the elimination method to solve this system as the variable $x$ gets eliminated on adding the equations after transformation.

No, the elimination method wouldn’t have worked if the bottom equation was multiplied by 2. On this transformation, no variable will get eliminated on adding the transformed equations.

Let the number of chickens is $x$ and number of sheeps is $y$. Now, given that there are total 21 animals in the farm, which means we can write it in the form of equation as shown below

$$
x+y=21 text{ } text{ (1) }
$$

It is also given that there are total 56 legs. As a chicken has 2 legs and a sheep has 4, so we can represent this in terms of equation as shown below

$$
2x+4y=56 text{ } text{ ( 2)}
$$

Now, solving the equations for values of x and y.

$$
begin{align*}
x+y&=21\
x&=21-y\
text{putting this into equation (2)}\
2cdot (21-y)+4y&=56\
42-2y+4y &=56\
2y&=14\
y&=dfrac{14}{2}\
y&=7
end{align*}
$$

Putting the value of y=7 into the $x+y=21$, we can get the value of x.

$Rightarrow$
$$
begin{align*}
x+7&=21\
x&=21-7\
x&=14
end{align*}
$$

Hence, there are 14 chickens and 7 sheeps in the Cole’s farm.

$textbf{(a)}$ Given that motorboat travels 18 miles per hour in still water. Given that $w$ represents the speed of river current in miles per hour.

When boat travel downstream the current flow of the river will support the movement of the boat hence the speed of the river current will get added to the speed of the motorboat. The situation can be represented by the equation shown below.

$$
begin{align*}
text{speed}_d=(18+w) text{ miles per hour}
end{align*}
$$

When boat travel upstream the current flow of the river will oppose the movement of the boat hence the speed of the river current will get subtracted from the speed of the motorboat. The situation can be represented by the equation shown below.

$$
begin{align*}
text{speed}_u=(18-w) text{ miles per hour}
end{align*}
$$

$textbf{(b)}$ Given that the boat takes equal time to travel 49 miles upstream and 77 miles downstream.

We can use the formula
$$
text{distance}=text{speed} times text{time}
$$
to find the expressions in each situation. Let $t_u$ represents the time taken to travel 49 miles upstream and $t_d$ represents the time taken to travel 77 miles downstream.

$$
begin{align*}
49&=(18-w)times t_u\
77&=(18+w)times t_d
end{align*}
$$

We are given that $t_u=t_d$ So putting $t_u=t_d=t$ into the above system and simplyfy the brackets. The new system becomes

$$
begin{align*}
49&=18t-wt\
77&=18t+wt
end{align*}
$$

Now , we can use elimination method on the above system as shown in the steps ahead.

$$
begin{align*}
49&=18t-wt\
+(77)& +(18t+wt)\
49+77&=18t+18t-wt+wt\
126&=36t tag{divide each side by 36}\
dfrac{126}{36}&=dfrac{36t}{36}\
3.5&=t\
t&=3.5 text{ hours}
end{align*}
$$

Therefore, it will take 3.5 hours to th boat to travel 49 miles upstream and 77 miles downwards.

$textbf{(c)}$ Yes, we can also use both the Equal value method and Substitution method to solve this problem.

For Equal values method we can rearrange the equation in the form $t=$. Given that the time taken by both the boats is same so we can equate the expression of time and solve for $w$ first then for $t$.

For Substitution method we can subtistute the value of any variable from one equation into the other equation.

$textbf{(a)}$
$$
text{speed}_d=(18+w) text{ miles per hour}
$$

$$
text{speed}_u=(18-w) text{ miles per hour}
$$

$textbf{(b)}$ 3.5 hours

$textbf{(c)}$ Yes, we can also use both the Equal value method and Substitution method to solve this problem.

$textbf{a.}$

Yes, the system is a good candidate for the Elimination Method since they have the same term: $2n$. In this case, we let:

$$
begin{align}
5m+2n&=-10\
3m+2n&=-2
end{align}
$$

To eliminate $2n$, subtract each side of eq. (1) and (2) then solve for $m$:

$$
begin{align*}
2m&=-8\
m&=-4
end{align*}
$$

Solve for $n$ using any of the original equations. I used eq. (1):

$$
begin{align*}
5(-4)+2n&=-10\
-20+2n&=-10\
2n&=10\
n&=5
end{align*}
$$

$textbf{Check:}$ Substitute $m=-4$ and $n=5$ to the system of equations.

$$
begin{align*}
5(-4)+2(5)&=-10 & 3(-4)+2(5)&=-2\
-20+10&=-10 & -12+10&=-2\
-10&=-10hspace{5mm}checkmark & -2&=-2hspace{5mm}checkmark
end{align*}
$$

So, the solution of the system is:

$$
color{#c34632}m=4,n=5
$$

$textbf{b.}$

Yes, the system is a good candidate for the Elimination Method since they have opposite terms: $-b$ and $b$. In this case, we let:

$$
begin{align}
6a-b&=3\
b+4a&=17
end{align}
$$

To eliminate $b$, add each side of eq. (1) and (2) then solve for $a$:

$$
begin{align*}
10a&=20\
a&=2
end{align*}
$$

Solve for $b$ using any of the original equations. I used eq. (2):

$$
begin{align*}
b+4(2) &=17\
b+8 &=17\
b&=9
end{align*}
$$

$textbf{Check:}$ Substitute $a=2$ and $b=9$ to the system of equations.

$$
begin{align*}
6(2)-9&=3 & 9+4(2) &=17\
12-9&=3 & 9+8&=17\
3&=3hspace{5mm}checkmark & 17&=17hspace{5mm}checkmark
end{align*}
$$

So, the solution of the system is:

$$
color{#c34632}a=2,b=9
$$

$textbf{c.}$

No, the system is not a good candidate for the Elimination Method because they do not have the same term or opposite terms. However, we can make them so by multiply one equation by a factor. In this case, we first let:

$$
begin{align}
7x+4y&=17\
3x-2y&=-15
end{align}
$$

Multiplying eq. (2) by 2, we now have a system with opposite terms: eq. (1) and eq. (3)

$$
6x-4y=-30tag{3}
$$

To eliminate $4y$, add each side of eq. (1) and (3) then solve for $x$:

$$
begin{align*}
13x&=-13\
x&=-1
end{align*}
$$

Solve for $y$ using any of the original equations. I used eq. (1):

$$
begin{align*}
7(-1)+4y&=17\
-7+4y&=17\
4y&=24\
y&=6
end{align*}
$$

$textbf{Check:}$ Substitute $x=-1$ and $y=6$ to the system of equations.

$$
begin{align*}
7(-1)+4(6)&=17 & 3(-1)-2(6) &=-15\
-7+24&=17 & -3-12&=-15\
17&=17hspace{5mm}checkmark & -15&=-15hspace{5mm}checkmark
end{align*}
$$

So, the solution of the system is:

$$
color{#c34632}x=-1,y=6
$$

a. Yes ; $m=-4$, $n=5$

b. Yes ; $a=2$, $b=9$

c. No ; $x=-1$, $y=6$

$textbf{(a)}$

$$
begin{align*}
2x+3y&=9\
-3x+3y&=-6
end{align*}
$$

multiply the second equation by $-1$, it becomes $3x-3y=6$. Now we can use the elimination method for this system.

$$
begin{align*}
2x+3y&=9\
+(3x-3y)& +(6)\
2x+3x+3y-3y&=9+6\
5x&=15tag{divide each side by 5}\
dfrac{5x}{5}&=dfrac{15}{5}\
x&=3
end{align*}
$$

Now, put $x=3$ into equation (1) and solve for $y$.

$$
begin{align*}
2x+3y&=9\
2(3)+3y&=9\
6+3y&=9tag{subtract 6 from the each side}\
6-6+3y&=9-6\
3y&=3tag{divide each side by 3}\
dfrac{3y}{3}&=dfrac{3}{3}\
y&=1
end{align*}
$$

The solution point is $(3,1)$

$textbf{(b)}$
$$
begin{align}
x&=8-2y\
y-x&=4
end{align}
$$

We can use Substitution method to solve this system. Put the value of $x$ form the equation (1) into the equation (2).

$$
begin{align*}
y-x&=4\
y-(8-2y)&=4\
y-8+2y&=4tag{add 8 to the each side}\
3y-8+8&=4+8\
3y&=12tag{divide each side by 3}\
dfrac{3y}{3}&=dfrac{12}{3}\
y&=4
end{align*}
$$

Put $y=4$ into equation (1) to solve for $x$

$$
begin{align*}
x&=8-2y\
x&=8-2(4)\
x&=8-8\
x&=0
end{align*}
$$

The solution point is $(0,4)$

$textbf{(c)}$
$$
begin{align*}
y&=-dfrac{1}{2}x+7\
y&=x-8
end{align*}
$$

We can use Equal value method to solve this system of equation. We need to equate the $y=$ expression of the both equation

$$
begin{align*}
-dfrac{1}{2}x+7&=x-8tag{add $dfrac{1}{2}x+8$ to the each side}\
-dfrac{1}{2}x +dfrac{1}{2}x+7+8&=x +dfrac{1}{2}x-8+8\
15&=dfrac{2+1}{2}x\
15&=dfrac{3}{2}xtag{multiply each side by $dfrac{2}{3}$}\
15cdot dfrac{2}{3}&= dfrac{3}{2}x cdot dfrac{2}{3}\
10&=x\
end{align*}
$$

Put $x=10$ into equation (2) and solve for $y$

$$
begin{align*}
y&=x-8\
y&=10-8\
y&=2
end{align*}
$$

The solution point is $(10,2)$

$textbf{(d)}$

$$
begin{align}
9x+10y&=14\
7x+5y&=-3
end{align}
$$

Multiply equation (2) with -2

$$
begin{align*}
-2(7x+5y)&=-2(-3)\
-14x-10y&=6
end{align*}
$$

Now we can use the Elimination method for this new system with transformed equation $(2)$.

$$
begin{align*}
9x+10y&=14\
+(-14x-10y)& +(6)\
9x-14x+10y-10y&=14+6\
-5x&=20tag{divide each side by $-5$}\
dfrac{-5x}{-5}&=dfrac{20}{-5}\
x&=-4
end{align*}
$$

Now put $x=-4$ into equation (1) and solve for $y$.

$$
begin{align*}
9x+10y&=14\
9(-4)+10y&=14\
-36+10y&=14tag{add 36 to the each side}\
-36+36+10y&=14+36\
10y&=50tag{divide each side by 10}\
dfrac{10y}{10}&=dfrac{50}{10}\
y&=5
end{align*}
$$

The solution point is $(-4,5)$

$textbf{(a)}$ The solution point is $(3,1)$

$textbf{(b)}$ The solution point is $(0,4)$

$textbf{(c)}$ The solution point is $(10,2)$

$textbf{(d)}$ The solution point is $(-4,5)$

Given equations represent the straight lines, which only intersect at a single point. Therefore, two given lines can only have more than one solutions together when they are overlapping.

We can check the solutions by Aimee and Eric by putting these points into the equations and by checking its validity.

$bullet$ checking $(-4,-6)$ into $2x-3y=10$

$$
begin{align*}
2x-3y&=10\
2(-4)-3(-6)&=10\
-8+18&=10\
10&=10tag{ true}
end{align*}
$$

checking $(-4,-6)$ into $6y=4x-20$

$$
begin{align*}
6y&=4x-20\
6(-6)&=4(-4)-20\
-36&=-16-20\
-36&=-36tag{ true}
end{align*}
$$

We can see that the Aimee’s solution is satisfying both the given equations. Hence it is a valid solution point.

$bullet$ checking $(8,2)$ into $2x-3y=10$

$$
begin{align*}
2x-3y&=10\
2(8)-3(2)&=10\
16-6&=10\
10&=10tag{ true}
end{align*}
$$

checking $(8,2)$ into $6y=4x-20$

$$
begin{align*}
6y&=4x-20\
6(2)&=4(8)-20\
12&=32-20\
12&=-12tag{ true}
end{align*}
$$

The solution point of Eric is also satisfying the given equations. Therefore, $(8,2)$ is also a valid solution point.

As given system has more than one solution points together hence the line should be overlapping with each other.

In fact we can obtain the second equation by multiplying it with $-2$ and by rearranging it in $6y=$ form.

Given that Matilda and Nancy are 60 miles apart and they are bicycling toward each other on the same road. Matilda rides 12 miles per hour and Nancy rides at 8 miles per hour. As they both are riding towards each other and they are supporting to cover the distance together, therefore their speed should add up.

The relative speed of Matilda and Nancy is $12+8=20$ miles per hour.

We can find the time to cover the distance of 60 miles by using the formula.

$$
begin{align*}
text{Time}&=dfrac{text{Distance}}{text{speed}}\
text{Time}&=dfrac{60}{20}left (dfrac{text{miles}}{text{miles}/text{hour}} right)\
text{Time}&=3 text{hour}
end{align*}
$$

Therefore, It will take 3 hours for them to cover 60 miles and meet.

Let $t(n)$ represents the $n^text{th}$ term of the sequence. We are given several terms of the sequence on the graph. We can find the explicit equation for this sequence by the method shown below.

$$
begin{align*}
t(1)&=12\
t(2)&=36=12cdot 3=12 cdot 3^{2-1}\
t(3)&=108=12cdot 3cdot 3=12 cdot 3^{3-1}\
t(n)&=12cdot 3^{n-1}
end{align*}
$$

Threfore, the explicit equation for the given sequence is
$$
boxed{t(n)=12cdot 3^{n-1}}
$$

$$
t(n)=12cdot 3^{n-1}
$$

$textbf{(a)}$ For solving the given equation, we first need to solve the brackets terms then we put the variables at one side and constants on the other side like shown below.

$$
begin{align*}
10 – 2(2x+1)&=4(x-2) \
10-4x-2&=4x-8tag{text{on solving brackets}}\
8-4x&=4x-8 tag{text{add 8+4x to each side}}\
16&=8x \
x&=dfrac{16}{8}\
x&=2
end{align*}
$$

$textbf{(b)}$ Like above example for solving the given equation, we first need to solve the brackets terms then we put the variables at one side and constants on the other side like shown below.

$$
begin{align*}
5 – (2x-3)&=-8+2x\
5-2x+3&=-8+2x tag{text{on solving brackets}}\
-2x+8&=2x-8 tag{text{add 8+2x to each side}}\
16&=4x \
x&=dfrac{16}{4}\
x&=4
end{align*}
$$

$textbf{(a)}$ $x=2$

$textbf{(b)}$ $x=4$

$textbf{(a)}$

$$
begin{align*}
y&=mx+btag{subtract $mx$ from the both side}\
y-mx&=mx-mx+b\
y-&mx=btag{interchange sides}\
&boxed{b=y-mx}
end{align*}
$$

$$
textbf{(b)}
$$

$$
begin{align*}
y&=mx+btag{subtract $b$ from the both side}\
y-b&=mx+b-b\
y-b&=mxtag{divide both side by m}\
dfrac{y-b}{m}&=dfrac{mx}{m}\
dfrac{y-b}{m}&=x\
&boxed{x=dfrac{y-b}{m}}
end{align*}
$$

$textbf{(c)}$
$$
begin{align*}
I&=prttag{divide each side by $pr$}\
dfrac{I}{pr}&=dfrac{prt}{pr}\
dfrac{I}{pr}&=t\
&boxed{t=dfrac{I}{pr}}
end{align*}
$$

$textbf{(d)}$

$$
begin{align*}
A&=p+prttag{subtract $p$ from the both side}\
A-p&=p-p+prt\
A-p&=prttag{divide each side by $pr$}\
dfrac{A-p}{pr}&=dfrac{prt}{pr}\
dfrac{A-p}{pr}&=t\
&boxed{t=dfrac{A-p}{pr}}
end{align*}
$$

$textbf{(a)}$ $y-mx$

$textbf{(b)}$ $x=dfrac{y-b}{m}$

$textbf{(c)}$ $t=dfrac{I}{pr}$

$textbf{(d)}$ $t=dfrac{A-p}{pr}$

We can put value of x or y from one equation into the other equation to eliminate a variable and have an equation of single variable, like shown below

$$
begin{align}
4x+3y&=10\
9x-4y&=1
end{align}
$$

From equation (1), we can write
$$
x=dfrac{10-3y}{4}
$$
and
$$
y=dfrac{10-4x}{3}
$$

Now, putting $x=dfrac{10-3y}{4}$ into the equation (2), we can have an equation in terms of variable y only.

$$
begin{align*}
9x-4y&=1\
9(dfrac{10-3y}{4})-4y&=1\
dfrac{90}{4}-dfrac{27y}{4}-4y&=1\
90-27y-16y&=4\
43y&=86\
y&=dfrac{86}{43}\
y&=2
end{align*}
$$

Similarly, putting $y=dfrac{10-4x}{3}$ into the equation (2), we can have an equation in terms of variable x only.

$$
begin{align*}
9x-4(dfrac{10-4x}{3})&=1\
9x -dfrac{40}{3}+dfrac{16x}{3}&=1\
27x-40+16x &=3\
43x&=43\
x&=dfrac{43}{43}\
x&=1\
end{align*}
$$

$y=2$

$x=1$

Given that Blue paint comes in a 5-ounce container costing $2 per container. The containers of silver
paint hold two ounces and cost $3 per container. The art club spent $56 and bought a total of 74 ounces of paint.\
Let$x$represents the number of containers of the blue paint and$y$represents the number of containers of the silver paint.\
It is given that the art club spent total $56. So by multiplying the cost of each paint with the number of containers we can write the equation as$ $2x+3y=56$ $Now, The club bought a total of 74 ounces of paint. The equation representing this situation is$ $5x+2y=74$$
We can solve this system by using the Elimination method but for this, we need to modify our equations as shown below.

$$
begin{align*}
2x+3y&=56tag{multiply each side by 2}\
2(2x+3y)&=2(56)\
4x+6y&=112
end{align*}
$$

$$
begin{align*}
5x+2y&=74tag{multiply each side by 3}\
3(5x+2y)&=3(74)\
15x+6y&=222
end{align*}
$$

Now we have our system of the equations as

$$
begin{align*}
4x+6y&=112\
15x+6y&=222
end{align*}
$$

Subtract equation (1) from the equation (2), we get

$$
begin{align*}
15x+6y&=222\
-(4x+6y)& -(112)\
11x&=110tag{divide each side by 11}\
x&=10
end{align*}
$$

Now put $x=10$ into equation (1) to solve for $y$

$$
begin{align*}
4x+6y&=112\
4(10)+6y&=112\
40+6y&=112tag{subtract 40 from the each side}\
6y&=112-40\
6y&=72tag{divide each side by 6}\
dfrac{6y}{6}&=dfrac{72}{6}\
y&=12
end{align*}
$$

Therefore, the club bought 10 containers of the blue paint and 12 containers of the silver paint.

(a) We have given system as

$$
begin{align}
10x+4y&=-8\
5x+2y&=10
end{align}
$$

For solving this using elimination method we have to multiply the equation (2) with 2 and then subtract it from equation (1), which gives

$$
begin{align*}
10x+4y&=-8 tag{1}\
2cdot (5x+2y)&=cdot (10) tag{multiplying each side by 2}\
10x+4y&=20 tag{3}\
(10x+4y=-8) &- (10x+4y=20)\
text{It gives } & 0=-28\
end{align*}
$$

Hence , $textbf{no solution}$ for this system of equations.

$textbf{(b)}$ No, these do not represent the same line. Although the slope for both are the same but they have different y-intercepts.

$textbf{(c)}$ $10x+4y=-8$
$$
begin{align*}
y&=dfrac{-10x-8}{4}\
y&=-dfrac{5}{2}x -2tag{1}\
end{align*}
$$

$5x+2y=10$
$$
begin{align*}
y&=dfrac{-5x+10}{2}\
y&=-dfrac{5}{2}x +5tag{2}\
end{align*}
$$

We can see, that the slope for both the lines is same and y-intercept is different which means that the given lines are parallel to each other. Hence we got no solution in the part$textbf{ (a)}$.

$textbf{(a)}$ No solution

$textbf{ (b)}$ No, these do not represent the same line. Although the slope for both are the same but they have different y-intercepts.

$textbf{(c)}$ Slope for both the lines is same and y-intercept is different which means that the given lines are parallel to each other. Hence we got no solution in the part$textbf{ (a)}$.

$textbf{(a)}$ The given system of the equations is

$$
begin{align}
10x+4y&=-8\
5x+2y&=10
end{align}
$$

We can use the elimination method to solve the above system but first, we need to modify the equation (2) by multiplying it with (2).

$$
begin{align*}
5x+2y&=10\
2(5x+2y)&=2(10)\
10x+4y&=20
end{align*}
$$

now, we have our modified system of the equations as

$$
begin{align}
10x+4y&=-8\
10x+4y&=20
end{align}
$$

We can subtract the equation (1) from the equation (2) for eliminating the possible variables.

$$
begin{align*}
10x+4y&=20\
-(10x+4y)&=-(-8)\
10x-10x+4y-4y&=20+8\
0&=28tag{not true}
end{align*}
$$

We can see that both the variables got canceled together and we got and we got a non-true equation. hence the given system has no solution. These lines should be parallel to each other.

$textbf{(b)}$ No, these equations do not represent the same line but they represent the parallel line. We can verify this by writing the equations in $y=mx+c$ form where $m$ represents the slope of the line and $c$ represents the $y$-intercept. We will see that the slope of the lines is the same but these have different values for $y$-intercepts. That is why these lines are parallel.

$textbf{(c)}$
$bullet$ Rearranging $10x+4y=-8$

$$
begin{align*}
10x+4y&=-8tag{subtract $10x$ from the each side}\
10x-10x+4y&=-10x-8\
4y&=-10x-8tag{divide each side by 4}\
y&=dfrac{-10x}{4}-dfrac{8}{4}\
y&=-dfrac{5}{2}x-2
end{align*}
$$

$bullet$ Rearranging $5x+2y=10$

$$
begin{align*}
5x+2y&=10tag{subtract $5x$ from the each side}\
5x-5x+2y&=-5x+10\
2y&=-5x+10tag{divide each side by 2}\
y&=dfrac{-5x}{2}+dfrac{10}{2}\
y&=-dfrac{5}{2}x+5
end{align*}
$$

On comparing with $y=mx+b$ we can see that both the above lines have same slope but diffrent $y$- intercept and hance these do not represent the same lines but represents parallel lines. These are the parallel lines which will never intersect any point and hence no possible solution for this system of the equations.

$textbf{(a)}$ Both the variables got canceled together and resulted in No solution.

$textbf{(b)}$ No, they represent parallel lines.

$textbf{(c)}$ These are the parallel lines which will never intersect any point and hence no possible solution for this system of the equations.

textbf{(a)}\ $10x-4y=8$\
begin{tabular}{ |p{1cm}|p{1cm}|}
hline
x & y \
hline
-6 & -17 \
hline
-4 & -12 \
hline
-2 & -7 \
hline
0 &-2\
hline
2&3\
hline
4&8\
hline
end{tabular}\\

$y=dfrac{5}{2}x-2$\
begin{tabular}{ |p{1cm}|p{1cm}|}
hline
x & y \
hline
-6 & -17 \
hline
-4 & -12 \
hline
-2 & -7 \
hline
0 &-2\
hline
2&3\
hline
4&8\
hline
end{tabular}\
\
From the tables, we can see that the solutions for each line are the same. Hence both the lines should be coinciding and infinite solutions for this system of equations.\

$textbf{(b)}$ Given system of equations coincides with each other and have infinite solutions.

$textbf{(c)}$
$$
begin{align}
10x-4y&=8\
y=dfrac{5}{2}x&-2
end{align}
$$

Equation (1) can be rearranged and can be written as $y=dfrac{5}{2}x-2$, say it equation (3).
Now, we use Elimination method by multiplying either of the equation (2) or (3) and add into the other. All the terms get cancelled and we will get

$$
0=0
$$
which is true for all the situation and hence infinite solutions.

$textbf{(a)}$ Infinite solutions.

$textbf{(b)}$ Coinciding lines

$textbf{(c)}$ We get equation like $0=0$, which is true for all cases and hence it justifies the infinite solutions.

$textbf{(a)}$ For solving such equation, we apply the distributive property in which we first choose one term from a bracket then multiply it by each terms in other bracket then we go for the next term and then multiply it by each terms in other bracket.

$$
begin{align*}
&(2x+1)(3x-2)\
&=2xcdot( 3x-2) +1cdot (3x-2) tag{text{Distributive property}}\
&=2xcdot 3x + 2xcdot -2 + 3x -2 tag{text{on opening the brackets}}\
&= 6x^2 -4x+3x-2\
&=6x^2-x-2\
end{align*}
$$

$textbf{(b)}$ Like above example for solving such equation, we apply the distributive property in which we first choose one term from a bracket then multiply it by each terms in other bracket then we go for the next term and then multiply it by each terms in other bracket.

$$
begin{align*}
&(2x+1)(3x^2-2x-5)\
&=2xcdot (3x^2-2x-5) + 1cdot (3x^2-2x-5) tag{text{Distributive property}}\
&=(2xcdot 3x^2 + 2xcdot -2x +2xcdot -5) +(3x^2-2x-5) tag{text{solving brackets}}\
&=6x^3 -4x^2 -10x + 3x^2-2x-5\
&=6x^3 -x^2 – 12x -5\
end{align*}
$$

$textbf{(a)}$ $6x^2-x-2$

$textbf{(b)}$ $6x^3 -x^2 – 12x -5$

$textbf{(a)}$ The given pair of equation are
$$
begin{align}
x&=-2y-3\
4y&-x=9
end{align}
$$
The point of intersection of the given pair of lines can be found out by putting equation (1) into the equation (2), which will result in terms of variable y only, which is shown below

$$
begin{align*}
4y-(-2y-3)&=9\
4y+2y+3&=9\
6y&=6\
y&=dfrac{6}{6}\
y&=1\
text{now putting $y=1$ into equation (1)}
Rightarrow \
x&=-2cdot 1-3\
x&=-2-3\
x&=-5
end{align*}
$$

For checking solutions, we can put $(x,y)=(-5,1)$ into any equation given equation to see if it holds true. If the solution satisfies it then we have a correct solution.

Now, putting $(x,y)=(-5,1)$ into equation (1), we get
$$
(-5=-2cdot 1 -3)=-5
$$

The solution satisfying the equations hence it is correct.

$textbf{(b)}$ The given pair of equation are
$$
begin{align}
x+5y&=8\
-x+2y&=-1
end{align}
$$
The point of intersection of the given pair of lines can be found out by equation (1) with the equation (2), which will result in cancelling of terms of variable $x$, and it remains in terms of $y$ only, which is shown below

$$
begin{align*}
7y&=7tag{text{adding eq(1) and eq(2)}}\
y&=dfrac{7}{7}\
y&=1\
text{now putting $y=1$ into equation (1)}
Rightarrow \
x+5&=8\
x&=8-5\
x&=3
end{align*}
$$

For checking solutions, we can put $(x,y)=(-5,1)$ into any equation given equation to see if it holds true. If the solution satisfies it then we have a correct solution.

Now, putting $(x,y)=(3,1)$ into equation (2), we get
$$
(-3 +2cdot 1= -1)=-1
$$

The solution satisfying the equations hence it is correct.

$textbf{(c)}$ The given pair of equation are
$$
begin{align}
4x-2y&=5\
y=2x &+10
end{align}
$$
The point of intersection of the given pair of lines can be found out by putting equation (2) into the equation (1), which will result in terms of variable y only, which is shown below

$$
begin{align*}
4x -2(2x+10)&=5\
4x -4x -20&=5\
-20&=5\
end{align*}
$$

which means that given set of equations has $textbf{no solution}$

We can rearrange the equation (1) as $y=2x+dfrac{5}{2}$

Now, we can see that the given pair has same slope but different y-intercept, which means they can never intersect and hence, their set having no solution is justified.

$textbf{(a)}$ $(x,y)=(-5,1)$

$textbf{(b)}$ $(x,y)=(3,1)$

$textbf{(c)}$ No solution

A function is defined as a relation between the output and input such that corresponding to every input there is only a single possible output.

$textbf{(a)}$ The given graph has more than one outputs corresponding to the inputs between $-3$ to $+3$. For example for the Input $x=0$ the possible outputs are $3$ and $-3$. Therefore, this graph does not represent a function.

Domain $rightarrow$ $(-3,3)$

Range $rightarrow$ $(-3,3)$

$textbf{(b)}$ This graph represents a function as corresponding to each input ($x$) there is only one output $(y)$.

Domain $rightarrow$ $(-3,3)$

Range $rightarrow$ $(-2,2)$

$textbf{(a)}$ No, the graph does not represents a function.

Domain $rightarrow$ $(-3,3)$

Range $rightarrow$ $(-3,3)$

$textbf{(b)}$ Yes, the graph represents a function.

Domain $rightarrow$ $(-3,3)$

Range $rightarrow$ $(-2,2)$

Pearson’s $textbf{r}$ for the given scatterplot is seems to close to be $textbf{zero}$ as there seems no linear relationship between the variables.

LSRL equation for this scatterplot can $y=4$, as it is the most repeated output for many given inputs(Shoe size(s)).
As there are lot of points on the scatterplot hence we cannot find answers exactly and that is why we are asked to make a conjecture only.

$bullet$ $textbf{r}$=0

$bullet$ LSRL equation for the scatterplot can be $y=4$

$textbf{(a)}$ $mangle 1$ and $mangle 4$ constitute the pair of corresponding angles between two given parallel lines, therefore they should be equal.

$$
Rightarrow mangle 1=mangle 4=74 text{textdegree}
$$

which means, we can write it as below
$$
begin{align*}
74text{textdegree} &= 3x-18text{textdegree}\
3x&=92text{textdegree}\
x&=dfrac{92}{3} text{textdegree}\
x&=33.67text{textdegree}
end{align*}
$$

$textbf{(b)}$ $mangle 1$ and $mangle 2$ constitute the pair of alternate interior angles between two given parallel lines, therefore they should be equal.

$$
Rightarrow mangle 1=mangle 2
$$

Using above relation in the given equations of $mangle 1$ and $mangle 2$ we can write as below

$$
begin{align*}
3x-9text{textdegree} &= x+25text{textdegree}\
2x&=25text{textdegree}+9text{textdegree}\
2x&=34text{textdegree}\
x&=dfrac{34}{2}text{textdegree}\
x&=17text{textdegree}
end{align*}
$$

$textbf{(a)}$ 33.67 $text{textdegree}$

$textbf{(b)}$ 17 $text{textdegree}$

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
frac{1}{6}m-3=-5& {;}quad : frac{1}{6}m-3+3=-5+3tag{Add 3 to both sides}\
&frac{1}{6}m=-2tag{Simplify} \
&6cdot frac{1}{6}m=6left(-2right)tag{Multiply both sides by 6} \
&{color{#c34632}m=-12}
end{align*}
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
frac{2}{3}x-3=frac{1}{2}x-7& {;}quad : frac{2}{3}x-3+3=frac{1}{2}x-7+3tag{Add 3 to both sides}\
&frac{2}{3}x=frac{1}{2}x-4tag{Simplify} \
&frac{2}{3}x-frac{1}{2}x=frac{1}{2}x-4-frac{1}{2}xtag{Subtract 1/2x from both sides} \
&frac{1}{6}x=-4tag{Simplify} \
&6cdot frac{1}{6}x=6left(-4right)tag{Multiply both sides by 6 } \
&{color{#c34632}x=-24}
end{align*}
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
x+frac{x}{2}-4=frac{x}{4}& {;}quad : xcdot :4+frac{x}{2}cdot :4-4cdot :4=frac{x}{4}cdot :4tag{Multiply both sides by 4}\
&4x+2x-16=xtag{Refine} \
&6x-16+16=x+16tag{Add 16 to both sides} \
&6x=x+16tag{Simplify} \
&6x-x=x+16-xtag{Subtract x from both sides } \
&5x=16tag{Simplify} \
&frac{5x}{5}=frac{16}{5}tag{Divide both sides by 5} \
&{color{#c34632}x=frac{16}{5}}
end{align*}
$$

$$
color{#4257b2} text{ a) }m=-12
$$

$$
color{#4257b2} text{ b) }x=-24
$$

$$
color{#4257b2}text{ c) } x=frac{16}{5}
$$

$textbf{(a)}$ Let $x$ represents the number of bottles Erica successfully capped and $y$ represents the bottled she broked. On the given day total number of bottles that came her way was 15.

$$
Rightarrow
$$

$$
x+y=15
$$

Now, Erica gets paid 4textcent for each bottle she successfully caps, but her boss deducts 2textcent from her pay for each bottle she breaks.
She made 6textcent today. This can be written in the form of equation as shown below.
$$
4x-2y=6
$$

Therefore, the system of equation is

$$
begin{align*}
x+y&=15\
4x-2y&=6
end{align*}
$$

$textbf{(b)}$

$bullet$ Solving using Elimination method.

We need to multiply the first equation by $2$.

$$
begin{align*}
x+y&=15\
2(x+y)&=2(15)\
2x+2y&=30
end{align*}
$$

Now we can add the modfied equation into the second equation, this will eliminate the variable $y$.

$$
begin{align*}
4x-2y&=6\
+(2x+2y)& 30\
4x+2x-2y+2y&=6+30\
6x&=36tag{divide each side by 6}\
dfrac{6x}{6}&=dfrac{36}{6}\
x&=6
end{align*}
$$

Now, we put $x=6$ into the equation $x+y=15$ and solve for $y$

$$
begin{align*}
x+y&=15\
6+y&=15\
y&=9
end{align*}
$$

Therefore, Erica successfully capped 6 bottles and broke 9 bottles.

$bullet$ Solving using Substitution method.
We need to rearrange the equation $x+y=15$ in $y=$ form so that we can substitute value of $y$ into the other equation and can solve of $x$ from the resulting equation.

$$
begin{align*}
x+y&=15tag{subtract $x$ from the each side}\
x-x+y&=-x+15\
y&=-x+15
end{align*}
$$

Now, substitute $y=-x+15$ into the equation $4x-2y=6$.

$$
begin{align*}
4x-2y&=6\
4x-2y&=6\
4x-2(-x+15)&=6\
4x+2x-30&=6tag{add 30 to the each side}\
6x-30+30&=6+30\
6x&=36tag{divide each side by 6}\
dfrac{6x}{6}&=dfrac{36}{6}\
x&=6
end{align*}
$$

Now, we put $x=6$ into the equation $4x-2y=6$ and solve for $y$

$$
begin{align*}
4x-2y&=6\
4(6)-2y&=6\
24-2y&=6tag{subtract $24$ from the each side}\
24-24-2y&=6-24\
-2y&=-18tag{divide each side by -2}\
dfrac{-2y}{-2}&=dfrac{-18}{-2}\
y&=2
end{align*}
$$

Therefore, Erica successfully capped 6 bottles and broke 9 bottles.

$textbf{(a)}$ The system of equation is

$$
begin{align*}
x+y&=15\
4x-2y&=6
end{align*}
$$

$textbf{(b)}$ Erica successfully capped 6 bottles and broke 9 bottles.

$textbf{(a)}$ These pair of equation can be most conveniently be solved using $textbf{Substitution method}$. the variable $x$ is isolated hence equation (1) can be substituted into the equation (2).

$textbf{(b)}$ Elimination method will be best suited for solving these pairs of equation. Either of the equation can be multiplied and added to the other to obtain equation in single variable.

$textbf{(c)}$ Equal value method

Given pairs have the $x$ variable isolated hence these can be equated to solve for $y$.

$textbf{(d)}$ Substitution method

Variable $x$ is isolated into the equation (2), which can be substituted into the equation (1).

$textbf{(e)}$ Equal value method.

Equation (2) can be written as $d=5(7-w)$, now both the equation can be equated as the variable $d$ is isolated.

$textbf{(f)}$ Elimination method.

Multiply the equation (2) by -2 and it will result into the same equation as equation (1). hence these lines coincides.

$textbf{(g)}$ Substitution method.

Any of the equation can be used to isolate a variable and can be substituted into the other.

$textbf{(h)}$ Equal value method

Equation (2) can be rearranged to isolate the variable $y$ after that equal value method can be used to solve the given pair.

$textbf{(a)}$ Substitution method

$textbf{(b)}$ Elimination method

$textbf{(c)}$ Equal value method

$textbf{(d)}$ Substitution method

$textbf{(e)}$ Equal value method

$textbf{(f)}$ Elimination method

$textbf{(g)}$ Substitution method

$textbf{(h)}$ Equal value method

Solving Systems of Equations

* $bullet$ Substitution method is used when one variable is isolated and the values indicated by that variable will be substituted to the other equation.

Example:

$$
3x – 2y = 1 text { and } y = x + 1
$$

$$
begin{align*}
3x – 2left(x + 1 right) & = 1 && {text {substitute for the given value of $y$}} \
3x – 2x – 2 & = 1 && {text {evaluate}} \
x – 2 + 2 & = 1 + 2 && {text {add 2 to both sides of the equation}} \
x & = 3 && {text {value of $x$}} \\
y & = 3 + 1 && {text {substitute for the given value}} \
y & = 4 && {text {value of $y$}}
end{align*}
$$

* $bullet$ Elimination method is used when adding or subtracting equations from each other to remove one variable.
Example:

$$
x + 2y = 3 text { and } 2x – 2y = 3
$$

$$
begin{align*}
x + 2y & = 3 && \
2x – 2y & = 3 && \\
3x & = 6 && {text {difference of both equations}} \
dfrac {3x}{3} & = dfrac {6}{3} && {text {divide both sides of the equation by 3}} \
x & = 2 && {text {value of $x$}} \\
2 + 2y & = 3 && {text {substitute for the given value}} \
2 + 2y – 2 & = 3 – 2 && {text {subtract 2 from both sides of the equation}} \
2y & = 1 && {text {simplify}} \
dfrac {2y}{2} & = dfrac {1}{2} && {text {divide both sides of the equation by 2}} \
y & = dfrac {1}{2} && {text {value of $y$}}
end{align*}
$$

* $bullet$ Equal values method is used by writing the equations in slope intercept form then set the two equations equal to each other.

Example:

$$
y = -x + 7 text { and } y = 2x + 1
$$

$$
begin{align*}
-x + 7 & = 2x + 1 && {text {make the equations equal to each other}} \
-x + 7 – 7 & = 2x + 1 – 7 && {text {subtract 7 from both sides of the equation}} \
-x – 2x & = 2x – 6 – 2x && {text {subtract $2x$ from both sides of the equation}} \
-3x & = -6 && {text {simplify}} \
dfrac{-3x}{-3} & = dfrac {-6}{-3} && {text {divide both sides of the equation by $-3$}} \
x & = 2 && {text {value of $x$}} \\
y & = -2 + 7 && {text {substitute for the given value}} \
y & = 5 && {text {value of $y$}}
end{align*}
$$

$textbf{(a)}$
$$
begin{align*}
-2x+3y&=1\
2x+6y&=2
end{align*}
$$

We can use elimination method to solve this system. Combine both the equations then solve for $y$.

$$
begin{align*}
-2x+3y&=1\
+(2x+6y)& +(2)\
-2x+2x+3y+6y&=1+2\
9y&=3tag{ divide each side by $9$}\
y&=dfrac{3}{9}\
y&=dfrac{1}{3}
end{align*}
$$

Put $y=dfrac{1}{3}$ into the first equation and solve for $x$

$$
begin{align*}
-2x+3y&=1\
-2x+3(dfrac{1}{3}&=1\
-2x+1&=1tag{subtract 1 from the each side}\
-2x+1-1&=1-1\
-2x&=0tag{divide each side by $-2$}\
x&=dfrac{0}{-2}\
x&=0
end{align*}
$$

The solution point is $(0,dfrac{1}{3})$

$textbf{(b)}$
$$
begin{align*}
y&=dfrac{1}{3}x+4\
x&=-3y
end{align*}
$$

We can solve this system using Substitution method. Substitute the value of $x$ from the second equation into the first.

$$
begin{align*}
y&=dfrac{1}{3}x+4\
y&=dfrac{1}{3}(-3y)+4\
y&=-y+4tag{ add $y $ to the each side}\
y+y&=-y+y+4\
2y&=4tag{ divide each side by $2$}\
dfrac{2y}{2}&=dfrac{4}{2}\
y&=2
end{align*}
$$

Put $y=2$ into second equation and solve for $x$

$$
begin{align*}
x&=-3y\
x&=-3(2)\
x&=-6
end{align*}
$$

The solution point is $(-6,2)$.

$textbf{(c)}$
$$
begin{align*}
3x-y&=7\
y=3x&-2
end{align*}
$$

We can rearrange the second equation to write it as $-3x+y=-2$. Now can combine both the equation to eliminate the possible variable.

$$
begin{align*}
3x-y&=7\
+(-3x+y)& +(-2)\
3x-3x-y+y&=7-2\
0 ne 5
end{align*}
$$

The given system of equations has no solutions.

$textbf{(d)}$
$$
begin{align*}
x+2y&=1\
3x+5y&=8
end{align*}
$$

Rearrange the first equation.in $x=$ form

$$
begin{align*}
x+2y&=1tag{subtract $2y $ form the each side}\
x+2y-2y&=-2y+1\
x&=-2y+1
end{align*}
$$

Now substitute the $x=-2y+1$ into the second equation.

$$
begin{align*}
3x+5y&=8\
3(-2y+1)+5y&=8\
-6y+3+5y&=8\
-y+3&=8tag{subtract $ 3$ form the each side}\
-y+3-3&=8-3\
-y&=5tag{ multiply each side by $ -1$}\
-ycdot -1&=5cdot -1\
y&=-5
end{align*}
$$

Now, put $y=-5$ into $x=-2y+1$ and solve for $x$.

$$
begin{align*}
x&=-2y+1\
x&=-2(-5)+1\
x&=10+1\
x&=11
end{align*}
$$

Therefore, the solution point is $(11,-5)$

$textbf{(a)}$ The solution point is $(0,dfrac{1}{3})$.

$textbf{(b)}$ The solution point is $(-6,2)$.

$textbf{(c)}$ The given system of equations has no solutions.

$textbf{(d)}$ The solution point is $(11,-5)$.

Let the pieces of nectarines requires is $x$

$Rightarrow$ Pieces of peached required $=2x$
It is said that number of total fruits required is 168, then we can represent the situation as below

$$
begin{align*}
x+2x&=168\
3x&=168\
x&=dfrac{168}{3}\
x&=56
end{align*}
$$

Hence, the total number of nectarines required is 56.

$textbf{(a)}$ Yes, she can substitute $3y$ for $2x-1$. It is because the first equation of the given system is $2x-1=3y$. So from this equation we know that $3y$ is equivalent to $2x-1$.

$textbf{(b)}$ Substitute $3y$ for $2x-1$ into the equation $5(2x-1)+y=32$ and solve for $y$.

$$
begin{align*}
5(2x-1)+y&=32\
5(3y)+y&=32\
16y&=32tag{ divide each side by $16 $}\
dfrac{16y}{16}&=dfrac{32}{16}\
y&=2
end{align*}
$$

Now put $y=2$ into the equation $2x-1=3y$ and solve for $y$.

$$
begin{align*}
2x-1&=3y\
2x-1&=3(2)\
2x-1&=6tag{ add $ 1$ to the each side}\
2x-1+1&=6+1\
2x&=7tag{ divide each side by $2 $}\
dfrac{2x}{2}&=dfrac{7}{2}\
x&=3.5
end{align*}
$$

The solution point is $(3.5 , 2)$

$textbf{(a)}$ Yes

$textbf{(b)}$ The solution point is $(3.5 , 2)$

Given graph is for the two variables, and appear as straight line,hence we can represent it as below

$$
t(n)=c_1cdot n + c_2
$$

where, $c_1$ and $c_2$ can be found out by putting any 2 given points on the graph into the function $t(n)$ and if the 3rd point also satisfy the equation then its the correct representation.
Given points are (1,4), (2,10) and (3,16). Now, solving for $c_1$ and $c_2$

$$
begin{align*}
4&=c_1cdot 1 + c_2tag{text{for point (1,4) } }\
10&=c_1cdot 2 +c_2 tag{text{ for point (2,10)}}
end{align*}
$$

$$
begin{align*}
c_2&=4-c_1 tag{text{using first equation}}\
10&=c_1cdot 2 + 4-c_1\
10-4&=c_1\
c_1&=6\
Rightarrow c_2&=4-6\
c_2&=-2
end{align*}
$$

Therefore the final equation becomes $t(n)=6cdot n -2$
we can see that it satisfy the point (3,16) as $6cdot 3 -2=18-2=16$, hence it is the correct function.

$$
t(n)=6cdot n -2
$$

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

Now, we have given points as $(0,6)$ and $(4,0)$. Let $(x_1,y_1)=(0,6)$ and $(x_2,y_2)=(4,0)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{0-6}{4-0}\
&=dfrac{-6}{4}\
&=-dfrac{3}{2}
end{align*}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Therefore, the equation of a line of slope $-dfrac{3}{2}$ passing through a point $(0,6)$ is given by

$$
begin{align*}
y-6&=-dfrac{3}{2}cdot (x-0)\
y-6&=-dfrac{3}{2}cdot x\
&boxed{y=-dfrac{3}{2}cdot x+6}
end{align*}
$$

$$
y=-dfrac{3}{2}cdot x+6
$$

$textbf{(a)}$

$$
begin{align*}
&2x(x+3)tag{use distributive property}\
&=2xcdot x+2xcdot 3\
&=2x^2+6x
end{align*}
$$

$textbf{(b)}$

$$
begin{align*}
&(3x+2)(x-3)\
&=3x(x-3)+2(x-3)\
&=3xcdot x+3xcdot -3+2cdot x+2cdot -3\
&=3x^2-9x+2x-6\
&=3x^2-7x-6
end{align*}
$$

$textbf{(c)}$
$$
begin{align*}
4y-2(6-y)&=6\
4y-2cdot 6 -2cdot -y&=6\
4y-12+2y&=6\
6y-12&=6tag{add $ 12$ to the each side}\
6y-12+12&=6+12\
6y&=18tag{ divide each side by $6 $}\
dfrac{6y}{6}&=dfrac{18}{6}\
y&=3
end{align*}
$$

$$
textbf{(d)}
$$

$$
begin{align*}
x(2x-4)&=(2x+1)(x-2)\
xcdot 2x+xcdot -4&=2x(x-2)+1(x-2)\
2x^2-4x&=2xcdot x+2xcdot -2+1cdot x+1cdot -2\
2x^2-4x&=2x^2-4x+x-2tag{subtract $2x^2-4x$ form the each side}\
(2x^2-4x)-(2x^2-4x)&=(2x^2-4x)-(2x^2-4x)+x-2\
0&=x-2tag{ add $2 $ to the each side}\
0+2&=x-2+2\
2&=x\
x&=2
end{align*}
$$

$textbf{(a)}$ $2x^2+6x$

$textbf{(b)}$ $3x^2-7x-6$

$textbf{(c)}$ $y=3$

$textbf{(d)}$ $x=2$

$textbf{(b)}$ We can check the validity of Brianna’s equation by putting the given data points in the given equation. If these points satisfy then Brianna’s equation is correct otherwise not.

$$
begin{align*}
4y-6x&=4
end{align*}
$$

putting point (2,4) into the equation.

$$
begin{align*}
(4cdot 4 -6cdot 2)&=4\
16-12&=4\
4&=4
end{align*}
$$

Hence, (2,4) satisfies the Brianna’s equation.

Now putting (6,10) into the above equation

$$
begin{align*}
(4cdot 10 -6cdot 6)&=4\
40-36&=4\
4&=4
end{align*}
$$

Point (6,10) also satisfies equation $4y-6x=4$.

Now, checking for the final point (20,31)

$$
begin{align*}
(4cdot 31-6cdot 20)&=4\
124-120&=4\
4&=4
end{align*}
$$

All the points satisfy the equation given by Brianna, hence it is the valid equation.

$textbf{(c)}$ Given that Antenna length is 1 mm that means $x=1$, we need to find the $y$

$$
begin{align*}
4y-6cdot 1&=4\
4y-6&=4\
4y&=10\
y&=dfrac{10}{4}\
y&=2.5 text{mm}
end{align*}
$$

Therefore , if a ladybug has an antenna 1 mm long then its legs will be of 2.5 mm long.

Also from the graph we can see that, it holds true.

$textbf{(b)}$ Brianna’s equation is correct, as it is true for all the given data points.

$textbf{(c)}$ 2.5 mm

First we are going to represent the total possible cost for a phone call by given call rates for different companies using equations.

For TeleTalks
$$
text{Total cost } = 8times t text{ textcent }
$$

For AmeriCall
$$
text{Total cost} = (5times t+30) text{ textcent }
$$

For CellTime
$$
text{Total cost} = (3times t+60) text{ textcent }
$$
Where, for all $t$ is time in minutes.

We are going to make the graph of the above functions, then we can see that trends of the total cost with the time for different companies. Whichever function is giving the lower cost for a specific time range will be suitable.

From the graph attached below, we can see that the trend of total cost of the call for the different companies with the increasing time.

$bullet$Now, we can observe that for the time upto 10 minutes the call cost via TeleTalks is lower than the other two companies.

$bullet$ From 10 minutes to upto 15 minutes the call cost is lowest for the calls done via AmeriCall.

$bullet$ From more than 15 minutes call time, call cost via CellTime is lower than the other providers.
So, following the information of graph Gemma should use TeleTalks if her call duration is lower than 10 minutes. If her calls generally last between 10 to 15 minutes then she should choose Americall. If her calls last for more than 15 minutes then she should choose Celltimes as provider.

Moreover, this can also be Solved by finding the points via solving equations above, where total cost of from different companies becomes equal and then comparing the total cost for different companies for time less and above than that. It will give the boundary points and trends can be seen.

Two parallel lines have same slopes and the two perpendicular lines have the product of their slope equal to $-1$.

We need to find the slope of each line and compare if the slopes are equal or not. If they are not equal then we check for the product of their slope.

The general form equation of any line is given by $y=mx+c$ where $m$ represents the slope of the line and $c$ represents the $y$-intercept. We rearrange each of the equation in this form so that we can compare and find the slopes.

$$
textbf{(a)}
$$

$$
begin{align*}
-3x+y&=5tag{ add $3x $ to the each side}\
-3x+3x+y&=3x+5\
y&=3x+5
end{align*}
$$

On comparing it with $y=mx+c$ we get the slope of the line $-3x+y=5$ is equal to $3$.

$$
textbf{(b)}
$$

$$
begin{align*}
-5x+y&=3tag{ add $5x $ to the each side}\
-5x+5x+y&=5x+5\
y&=5x+5
end{align*}
$$

On comparing it with $y=mx+c$ we get the slope of the line $-5x+y=5$ is equal to $5$.

$$
textbf{(c)}
$$

$$
begin{align*}
x+5y&=-15tag{subtract $x $ form the each side}\
x-x+5y&=-x-15\
5y&=-x-15tag{ divide each side by $ 5$}\
dfrac{5y}{5}&=dfrac{-x-15}{5}\
y&=-dfrac{1}{5}x-3
end{align*}
$$

On comparing it with $y=mx+c$ we get the slope of the line $-3x+y=5$ is equal to $-dfrac{1}{5}$.

$$
textbf{(d)}
$$

$$
begin{align*}
-15x+5y&=-25tag{ add $15x $ to the each side}\
-15x+15x+5y&=15x-25\
5y&=15x-25tag{ divide each side by $ 5$}\
dfrac{5y}{5}&=dfrac{15x-25}{5}\
y&=dfrac{15}{5}x-dfrac{25}{5}\
y&=3x-5
end{align*}
$$

On comparing it with $y=mx+c$ we get the slope of the line $-3x+y=5$ is equal to $3$.

$bullet$ We can see that the slopes of the equations in the part $(a)$ and $(d)$ is the same. Hence these are parallel lines.

$bullet$ We can see that the product of lines in the part $(b)$ and $(c)$ is equal to $5 times -dfrac{1}{5}=-1$ and hence these are the perpendicular lines.

(a) and (d) $rightarrow$ parallel lines.

(b) and (c) $rightarrow$ perpendicular lines.

$textbf{(a)}$ From the graph on on proper scale, we can easily evaluate that, for 10 brownies the cost is $18. Hence, Sue should charge $18 for 10 brownies.This could be also found out by making and solving equation for the given graph.\\
textbf{(b)} It is a proportional relationship as it is an equation of line passing through origin. The ratio is given by the slope of this line.\\
textbf{(c)} Slope of line passing through two points$(x_1,y_1)$and$x_2,y_2$is given by slope$=$dfrac{y_2-y_1}{x_2-x_1}]\
Here two points are$(0,0)$and$(12,21.6)$, therefore \$ $text{slope}=dfrac{21.6-0}{12-0}=1.8$ $Now, equation of line with slope 1.8 and passing through$(0,0)
$$
is given by
begin{align*}
y-0&=1.8(x-0)\
y&=1.8x
end{align*}
As we have given that during the last football game, Mary earned $34.2, which mean
$$
y=34.2$, so we can find the value of$x$ as shown below

$$
begin{align*}
34.2&=1.8x\
x&=dfrac{34.2}{1.8}\
x&=19
end{align*}
$$

There, during last football game Mary sold 19 brownies.

$textbf{(d)}$ The unit rate of change is 1.8 which is given by the slope of the line.

$textbf{(a)}$ $ 18

$textbf{(b)}$ Yes, it is a proportional relationship.

$textbf{(c)}$ During the last football game, Mary sold 19 Brownies.

$textbf{(d)}$ The unit rate of change is 1.8 which is given by the slope of the line.

Let $d$ represents the distance traveled by ship and yacht in miles when they meet and $t$ is the time taken in hours by the ship to reach this distance $d$. As the yacht left 3 hours later than the ship then the time taken by the yacht to cover the distance $d$ will be $t+3$. Therefore, we can represent the given situation with the help of the equations as shown below.

$$
text{Distance}=text{Speed}times text{Time}
$$

$bullet$ Equation for the cruise ship

$$
begin{align*}
d&=25times (t+3)
end{align*}
$$

$bullet$ Equation for the private yacht

$$
begin{align*}
d&=40times (t)
end{align*}
$$

Now, we can solve the equation using Equal value method. Equate $d$ from both the equation.

$$
begin{align*}
25times (t+3)&=40times (t)\
25t+75&=40ttag{subtract $25t$ form the each side}\
25t-25t+75&=40t-25t\
75&=15ttag{ divide each side by $15 $}\
dfrac{75}{15}&=dfrac{15t}{15}\
5&=t text{ hours}
end{align*}
$$

Now , put $t=5$ hours into the equation $d=40t$ to solve for $d$.

$$
begin{align*}
d&=40t\
d&=40(5)\
d&=200 text{ miles}
end{align*}
$$

Therefore, the yacht will overtake the cruise ship when they travel 200 miles from the Bahamas.

$$
textbf{(a)}
$$

$$
begin{align*}
y&=-2x+5tag{subtract $5$ form the each side}\
y-5&=-2x+5-5\
y-5&=-2xtag{ divide each side by $ -2$}\
dfrac{y-5}{-2}&=dfrac{-2x}{-2}\
dfrac{5-y}{2}&=x\
&boxed{x=dfrac{5-y}{2}}
end{align*}
$$

$textbf{(b)}$

$$
begin{align*}
m&=7-3(p-m)tag{simplify}\
m&=7-3p+3mtag{subtract $3m$ form the each side}\
m-3m&=7-3p+3m-3m\
-2m&=7-3ptag{subtract $7$ form the each side}\
-2m-7&=7-7-3p\
-2m&=-3ptag{multply each side by $-1$}\
(-2m-7)cdot -1&=-3pcdot -1\
2m+7&=3ptag{ divide each side by $3$}\
dfrac{2m+7}{3}&=dfrac{3p}{3}\
dfrac{2m+7}{3}&=p\
&boxed{p=dfrac{2m+7}{3}}
end{align*}
$$

$textbf{(c)}$

$$
begin{align*}
2(y-3)&=4\
2y-6&=4tag{ add $6$ to the each side}\
2y-6+6&=4+6\
2y&=10tag{ divide each side by $2$}\
dfrac{2y}{2}&=dfrac{10}{2}\
&boxed{y=5}
end{align*}
$$

$textbf{(d)}$

$$
begin{align*}
4(q-8)&=7q+5\
4q-32&=7q+5tag{subtract $4q$ form the each side}\
4q-4q-32&=7q-4q+5\
-32&=3q+5tag{subtract $5 $ form the each side}\
-32-5&=3q+5-5\
-37&=3qtag{ divide each side by $3$}\
dfrac{-37}{3}&=dfrac{3q}{3}\
dfrac{-37}{3}&=q\
&boxed{q=-dfrac{37}{3}}
end{align*}
$$

$textbf{(a)}$ $x=dfrac{5-y}{2}$

$textbf{(b)}$ $p=dfrac{2m+7}{3}$

$textbf{(c)}$ $y=5$

$textbf{(d)}$ $q=-dfrac{37}{3}$

The speed of the superhero is given $60,000$ meters per minute. We need to convert it in kilometers per hour as shown below.

We know that 1 km is equivalent to 1000 m and 1 hour has 60 minutes. We can find the speed in km per hour by using the method of Big Ones

$$
begin{align*}
60000left ( dfrac{ text{m}}{text{minutes}} right)&=60000left ( dfrac{ text{m}}{text{minutes}} right)times left ( dfrac{1 text{km}}{1000 text{m}} right) times left ( dfrac{60 text{minutes}}{text{1 hour}} right)\
&=60000times left ( dfrac{60}{1000} right) left ( dfrac{text{text{m}}}{text{m}} right)times left ( dfrac{text{minutes}}{text{minutes}} right)times left ( dfrac{text{km}}{text{ hour}} right)\
&=60cdot 60 left ( dfrac{text{km}}{text{ hour}} right)\
&=3600 left ( dfrac{text{km}}{text{ hour}} right)
end{align*}
$$

$textbf{(a)}$ They both need to complete the total distance of 40,075 km with each moving in opposite direction which means their speed should be added.

Let the $t$ represents the time taken by them to cover the total distance. Then we can represent the situation using the equation shown below.

$$
begin{align*}
3600cdot t+4415 cdot t&=40,075\
8015t&=40,075tag{ divide each side by $8015$}\
dfrac{8015t}{8015}&=dfrac{40,075}{8015}\
t&=5 text{ hours}
end{align*}
$$

$textbf{(b)}$ They both travelled for 5 hours. The distance covered by each of them can be found out using the formula.

$$
text{Distance}=text{Speed}times text{Time}
$$

We can find the individual distances, by putting respective speeds and the time 5 hours for each into the equation above.

$bullet$ Distance covered by the Superhero.

$$
begin{align*}
text{Distance}&= 3600times 5\
&=18,000 text{ km}
end{align*}
$$

$bullet$ Distance covered by the Superhero’s partner

$$
begin{align*}
text{Distance}&= 4415times 5\
&=22,075 text{ km}
end{align*}
$$

$textbf{(a)}$ 5 hours

$textbf{(b)}$ 18,000 km and 22,075 km respectively.

The first thing we need to know is that the hourly wage will change only at the integral value of years. This means if we try to represent the situation by an equation then the equation will represent a sequence which only takes integral inputs (years) and gives discrete outputs. This is because the hourly wage remains the same throughout the year and increases when the year changes.

Now, Let’s assume $t(n)$ represents the hourly wage in dollars and $n$ represents the number of years at the company. Then we can represent the situation as a sequence as shown below.

$$
begin{align*}
t(1)&=7\
t(3)&=8.50\
t(6)&=10.75\
t(7)&=11.50
end{align*}
$$

Let assume that the wage increases equally with each completing year. This means the sequence should be an Arithmetic sequence where each term can be obtained by adding a constant number (common difference) into the previous term. The common difference $(d)$ can be found out by taking the difference of any 2 consecutive terms like $d=t(n+1)-t(n)$.

The general term of an arithmetic sequence is given by

$$
t(n)=t(1)+(n-1)d
$$

For the given case, we have $t(1)=7$ and $d=t(7)-t(6)=11.50-10.75=0.75$. So put these values into the equation of general term.

$$
begin{align*}
t(n)&=t(1)+(n-1)d\
t(n)&=7+(n-1) 0.75
end{align*}
$$

Now, we need to verify the equation by checking it for $t(3)=8.50$ and $t(6)=10.75$.

$bullet$ Checking for $t(3)=8.50$

$$
begin{align*}
t(n)&=7+(n-1) 0.75\
t(3)&=7+(3-1)0.75\
8.50&=7+2cdot 0.75\
8.5&=7+1.5\
8.5&=8.5tag{True}\
end{align*}
$$

$bullet$ Checking for $t(6)=10.75$

$$
begin{align*}
t(n)&=7+(n-1) 0.75\
t(6)&=7+(6-1)0.75\
10.75&=7+5cdot 0.75\
10.75&=7+3.75\
10.75&=10.75tag{True}\
end{align*}
$$

Therefore, our general term for this sequence is true.

$textbf{(a)}$ After working for 5 years, the hourly rate can be found out by putting $n=5$ into the equation derived.

$$
begin{align*}
t(n)&=7+(n-1) 0.75\
t(5)&=7+(5-1) 0.75\
t(5)&=7+(4)cdot 0.75\
t(5)&=7+3\
t(5)&=10
end{align*}
$$

Therefore, Hector can expect to make $10 per hour after working at the company for 5 years.

$textbf{(b)}$ Yes, this is a proportional situation as the hourly rate is increasing constantly by $0.75 after the end of every year.\\
textbf{(c)} The hourly rate of the new employee can be found out by putting$n=0
$$
into the equation derived above. Because at the starting the number of years he worked at the company is 0.
begin{align*}
t(n)&=7+(n-1) 0.75\
t(0)&=7+(0-1)0.75\
t(0)&=7-0.75\
t(0)&=6.25
end{align*}
Now, given that he will work 20 hours a week with an hourly pay rate of $6.25\
$$
Rightarrow$

$$
begin{align*}
text{weekly earning}&=text{hourly rate}times text{number of hours of work in a week}\
&=6.25times 20\
&=125
end{align*}
$$

The new employee will earn $125 during the first week.

$textbf{(a)}$ Hector can expect to make $10 per hour after working at the company for 5 years.

$textbf{(b)}$ Yes, this is a proportional situation as the hourly rate is increasing constantly by $0.75 after the end of every year.

$textbf{(c)}$ The new employee will earn $125 during the first week.

The two parallel lines have the same slopes and the two perpendicular lines have the product of their slopes equal to $-1$.
Given that the center of the city is at $(0,0)$ and the main street had the equation $y=5x-3$.

$$
bullet
$$

Park Street is parallel to Main street which means it should have the slope equal to $5$ and it is also given that park street passes through the city center $(0,0)$.

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Therefore, the equation of a line of slope $5$ passing through a point $(0,0)$ is given by

$$
begin{align*}
y-(0)&=5cdot (x-0)\
y&=5cdot x\
&boxed{y=5x}
end{align*}
$$

Therefore, the equation for the Park Street is $y=5x$

$bullet$ Given that the Broadway is perpendicular to Main Street and has an ice cream shop five blocks north and five blocks east of city center. This means the slope $(m)$ of the equation for Broadway should follow
$mtimes 5=-1$ where $5$ is the slope of the main street line.

$Rightarrow$
$$
m=-dfrac{1}{5}
$$

Also, the Broadway line should pass through $(5,5)$ as Five blocks east means 5 units on the $x$-axis
and five blocks north means 5 units on the $y$-axis.

Now, The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Therefore, the equation of a line of slope $-dfrac{1}{5}$ passing through a point $(5,5)$ is given by

$$
begin{align*}
y-(5)&=-dfrac{1}{5}cdot (x-5)\
y-5&=-dfrac{1}{5}cdot x-dfrac{1}{5}cdot -5\
y-5&=-dfrac{1}{5}cdot x+1tag{ add $ 5$ to the each side}\
y-5+5&=-dfrac{1}{5}cdot x+1+5\
y&=-dfrac{1}{5}cdot x+6\
&boxed{y=-dfrac{1}{5}x+6}
end{align*}
$$

Therefore, the equation for the Broadway is $y=-dfrac{1}{5}x+6$.

$textbf{(a)}$ The equation for the Park Street is $y=5x$

$textbf{(b)}$ The equation for the Broadway is $y=-dfrac{1}{5}x+6$.

$$
y = 4x + 8
$$

$$
2x + 5y = 414
$$

where $y$ is the no of roses at $$5$ each and $x$ is the no of tulips $$2$ each.
Total cost of the flowers is $$414$.

Using substitution

$$
2x + 5(4x + 8) = 414
$$

$$
2x + 20x + 40 = 414
$$

$$
22x + 40 – 40 = 141 – 40
$$

$$
22x = 374
$$

$$
x = 17
$$

Substituting equation $1$ in equation $2$

$$
y = 4(17) + 8 =
76
$$

The number of roses sold were $76$

Substituting $x$ in equation $1$ to find $y$

Using elimination

$$
y = 4x + 8
$$

$$
-4x + y = 8
$$

Rewrite equation $1$

$$
2*(2x + 5y = 414)
$$

$$
4x + 10y = 828
$$

Multiply the equation by $2$

$$
-4x + y = 8
$$

$$
4x + 10y = 828
$$

$$
y + 10y = 8 + 828
$$

$$
11y = 836
$$

$$
y = dfrac{836}{11} =
76
$$

The number of roses sold were $76$

$$
x
$$

is eliminated as it has reversed coefficients.
Solve for $y$

$$
76
$$

Given that the airplane took six minutes to fly 2.2 miles with the wind. So we can find the speed of the wind by using the formula as shown below.
$$
text{Speed}=dfrac{text{Distance}}{text{Time}}
$$

First, we need to convert the time in hours as the quantities are given in miles and hours. 1 hour is equivalent to 60 minutes which implies $1text{ minute}=dfrac{1}{60}$ hour.

$Rightarrow$
$$
6text{ minute}=6cdot dfrac{1}{60}=dfrac{1}{10} text{ hour}
$$

Now, putting the known values, distance$=2.2$ miles and Time$=dfrac{1}{10}$ hour into the equation above.

$$
begin{align*}
text{Speed}&=dfrac{text{Distance}}{text{Time}}\
&=dfrac{2.2}{1/10}\
&=2.2cdot 10\
&=22 left ( dfrac{text{miles}}{text{hour}} right)
end{align*}
$$

Given that Lee’s model airplane flies at 18 miles per hour. We got final speed as 22 miles per hour which means that the wind is supporting the motion of the airplane hence the speed of the wind should be added to the speed of the airplane. Let $x$ represents the speed of the wind. Therefore, the net speed is equal to $18+x$ miles per hour.

$$
Rightarrow
$$

$$
begin{align*}
x+18&=22tag{subtract $ 18$ form the each side}\
x+18-18&=22-18\
x&=4
end{align*}
$$

Therefore, the wind was blowing with a speed of 4 miles per hour.

$textbf{(a)}$ We have pair of equations as

$$
begin{align}
6x-2y&=10\
3x-5& = y
end{align}
$$

For solving this set, we can multiply the equation (2) by $2$ and rearranged like shown below

$$
begin{align*}
2cdot(3x-5& = y)\
6x-10&=2y\
6x-2y&=10tag{text{rearranged (2)}}
end{align*}
$$

We can see that reformed equation (2) is exactly same as equation (1). Therefore this set equation has infinite solutions as they overlap with each other.

$textbf{(b)}$
We have given pair of equations as

$$
begin{align}
6x-2y&=5\
3x+2y &=-2
end{align}
$$

Adding Equation (1) and equation (2) will result in the equation in a single variable $x$ which can be solved for the intersection point $x$ and then for $y$.

$$
begin{align*}
6x-2y&=5\
+(3x+2y) &=+(-2)\
9x&=3\
x&=dfrac{3}{9}\
x&=dfrac{1}{3}
end{align*}
$$

On putting the value $x=dfrac{1}{3}$ into $6x-2y=5$, we can solve for $y$

$$
begin{align*}
6cdot (dfrac{1}{3})-2y&=5\
2-2y&=5\
-2y&=3\
y=&-dfrac{3}{2}
end{align*}
$$

Hence the solution point is $(dfrac{1}{3},-dfrac{3}{2})$.