$textbf{a.}$

Use any two points, say $(0,1)$ and $(2, 0)$ so that $Delta x=2-0=2$ and $Delta y=0-1=-1$. So, the slope is:

$$
m=dfrac{Delta y }{Delta x}=dfrac{-1}{2}=color{#c34632}-dfrac{1}{2}
$$

$textbf{b.}$

The $y$-intercept is where the graph intersects the $y$-axis. In this case, at:

$$
color{#c34632}(0,1)
$$

$textbf{c.}$

Use the equation of the line in the form $y=mx+b$ where $m=-dfrac{1}{2}$ (slope) and $b=1$ ($y$-intercept):

$$
color{#c34632}y=-dfrac{1}{2}x+1
$$

a. $-dfrac{1}{2}$

b. $(0,1)$

c. $y=-dfrac{1}{2}x+1$

$textbf{a.}$

In the equation of a line $y=mx+b$, $m$ represents the slope and $b$ represents the $y$-intercept. In this case,

$$
color{#c34632}m=2,b=1
$$

$textbf{b.}$

In the equation of a line $y=mx+b$, $m$ represents the slope and $b$ represents the $y$-intercept. In this case,

$$
color{#c34632}m=dfrac{2}{5},b=-4
$$

a. $m=2,b=1$

b. $m=dfrac{2}{5},b=-4$

The method I used to graph the lines is to use the slope and $y$-intercept that we found in the previous question.

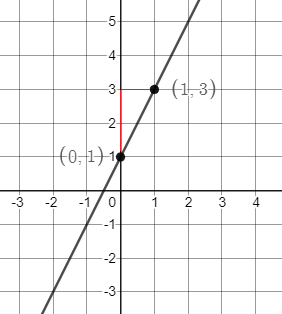
$textbf{a.}$

We have:

$$
m=2,b=1
$$

First, we plot the $y$-intercept, $(0,1)$. From this point, we locate another point by using the slope. That is, we move 2 units up and 1 unit to the right, locating $(1,3)$. Then, connect the two points with a straight line:

$textbf{b.}$

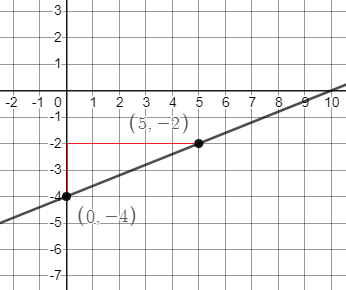
We have:

$$
m=dfrac{2}{5},b=-4
$$

First, we plot the $y$-intercept, $(0,-4)$. From this point, we locate another point by using the slope. That is, we move 2 units up and 5 units to the right, locating $(5,-2)$. Then, connect the two points with a straight line:

Hint: The method I used to graph the lines is to use the slope and $y$-intercept that we found in the previous question.

Using

$$
a^m cdot a^n=a^{m+n}
$$

$$
dfrac{a^m}{a^n}=a^{m-n}
$$

$$
(a^m)^n=a^{mn}
$$

$$
a^{-n}=dfrac{1}{a^n}
$$

a)
$$
dfrac{14a^3b^2}{21a^4b}=dfrac{14}{21} cdot a^{3-4}b^{2-1}=
dfrac{2}{3} cdot a^{-1}b^1=dfrac{2}{3}cdot dfrac{1}{a} cdot b=dfrac{2b}{3a}
$$

b)
$$
2m^3n^2 cdot 3mn^4=6m^{3+1}n^{2+4}=6m^4n^6
$$

c)
$$
dfrac{4x^{18}}{(2x^{22})^0}=dfrac{4x^{18}}{1}=4x^{18}
$$

(Using $a^0=1$)

d)
$$
(s^4tu^2)(s^7t^{-1})=s^{4+7}t^{1+(-1)}u^2=s^{11}t^0u^2=s^{11}u^2
$$

e)

$$
(3w^{-2})^4=3^4 w^{-2 cdot 4}=81 w^{-8}=dfrac{81}{w^8}
$$

f)
$$
m^{-3}=dfrac{1}{m^3}
$$

Given that, Shirley starts with $85 in the bank and saves $15 every two months.\\
Unit rate of change in the situation is given as $15 every two months, which is equal to slope of the line we intend to find.$ $text{Slope}=dfrac{15}{2}=7.5 dfrac{text{Dollars}}{text{month}}$ $\
Let$x$represents the months and$y$represent the money in $ in Shirley’s bank account in any given month, then the equation of line is can be written as$ $y=mx+c$ $where,$m$is the slope of the line and c is the$y$- intercept.\
We are given the slope as$7.5$and$c=$85$ is the y-intercept as it represent the account balance for starting month which is $x=0$. On putting these values into the equation, the final equation becomes

$$
y=7.5x+85
$$

$$
y=7.5x+85
$$

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

We can choose any two set of points from the table to find the slope.

$textbf{(a)}$ Let $(x_1,y_1)=(0,9)$ and $(x_2,y_2)=(1,4)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{4-9}{1-0}\
&=dfrac{-5}{1}\
&=-5
end{align*}
$$

$textbf{(b)}$ Let $(x_1,y_1)=(2,22)$ and $(x_2,y_2)=(4,40)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{40-22)}{4-2}\
&=dfrac{18}{2}\
&=9
end{align*}
$$

$textbf{(a)}$ -5

$textbf{(b)}$ 9

Let $x$ be the figure number and $y$ be the number of tiles so that the three figures correspond to the points:

$$
(1,6),(2,9),(3,12)
$$

Using any two points, say $(1,6)$ and $(2,9)$, we have $Delta x=2-1=1$ and $Delta y=9-6=3$. So, the slope is:

$$
m=dfrac{Delta y }{Delta x}=dfrac{3}{1}=3
$$

Use the equation of the line in the form $y=mx+b$. Substituting any of the two points and the slope, we can solve for $b$. I used $(x,y)=(1,6)$:

$$
begin{align*}
y&=mx+b\
6&=3(1)+b\
6&=3+b\
3&=b\
end{align*}
$$

So, the equation of the line (rule for the tile pattern) is:

$$
color{#c34632}y=3x+3
$$

For figure 58, $x=58$, there are:

$$
y=3(58)+3=174+3=color{#c34632}177text{ tiles}
$$

$y=3x+3$ where $x$ is the figure number and $y$ is the number of tiles ; 177 tiles

Slope of line passing through 2 given points $(x_1,y_1)$ and $(x_2,y_2)$ can be written as

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

Now, we have points as $(-5,7)$ and $(10,1)$

$Rightarrow$
$$
begin{align*}
text{slope}&=dfrac{1-7}{10-(-5)}\
&=dfrac{-6}{15}\
&=dfrac{-2}{5}\
end{align*}
$$

$$
-dfrac{2}{5}
$$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
& text{For x=-2 we solve this}\
&-3left(-2right)^2+4left(-2right)+5\\
&=-3cdot :4+4left(-2right)+5 tag{Calculate exponents} \
&=-12+4left(-2right)+5 tag{Multiply and Divide}\
&=-12-8+5 tag{Multiply and Divide}\\
&=boxed{{color{#c34632} -15 } }
end{align*}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
& text{For x=1 we solve this}\
&6-left(5cdot :1-9right)^2\\
&=6-left(-4right)^2 tag{Calculate within parentheses} \
&=6-16 tag{Calculate exponents}\\
&=boxed{{color{#c34632} -10 } }
end{align*}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
& text{For k=-8 we solve this}\
&frac{-4}{-8+7}\\
&=frac{-4}{-1} tag{Add/Subtract the numbers} \
&=frac{4}{1}\\
&=boxed{{color{#c34632} 4 } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{-a}{-b}=frac{a}{b}
$$

$$
color{#c34632} text{} mathrm{Apply:rule}:frac{a}{1}=a
$$

$$
text{}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
& text{For m=-2 and n=3 we solve this}\
&frac{2left(-2right)}{3-1}-left(-2right)^3-3\\
&=frac{-2cdot :2}{3-1}-left(-2right)^3-3 tag{Remove parentheses} \
&=-2-left(-2right)^3-3\
&=-2-left(-2^3right)-3\
&=-2+2^3-3 \
&=2^3-5 \
&=8-5 \\
&=boxed{{color{#c34632} 3 } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Apply:exponent:rule}:quad left(-aright)^n=-a^n,:mathrm{if:}nmathrm{:is:odd}
$$

$$
color{#c34632} text{} mathrm{Apply:rule}:-left(-aright)=a
$$

$$
text{}
$$

$$
{color{#4257b2}text{ e) }}
$$

$$
begin{align*}
& text{K, can not equal to -7 because denominator can not be 0 }
end{align*}
$$

$$
color{#4257b2} text{a)}-15
$$

$$
color{#4257b2} text{b)}-10
$$

$$
color{#4257b2}text{c)} 4
$$

$$
color{#4257b2} text{d)} 3
$$

$$
color{#4257b2} text{e)K, can not equal to -7 because denominator can not be 0}
$$

Given that a page contains an average of 300 words and it takes someone to read one page in 68 seconds.

$Rightarrow$ Words that can be read in 1 second is given by $dfrac{300}{68}$.

Words that can be read in 1 minute (60 seconds) is given by $dfrac{300}{68}times 60=264.7$

Therefore, a person can read around 265 words per minute of the given book.

$bullet$ Given that it takes 68 seconds to read a page, then number of pages that can be read in an hour can be found as shown below

$$
1 text{hour}=60times 60 =3600 text{seconds}
$$

$$
text{pages per second} = dfrac{1}{68}
$$

$$
text{pages in 3600 seconds} = dfrac{1}{68}times 3600=52.94
$$

Therefore, one can read around 53 pages of the book in an hour.