
All Solutions
Page 529: Closure Activity
$$
m=dfrac{Delta y}{Delta x }=dfrac{-2-0}{0-4}=dfrac{-2}{-4}=dfrac{1}{2}
$$
Since $b=-2$, then the equation is:
$$
y=dfrac{1}{2}x-2
$$
Since the line is dashed, the points on the line itself are not solutions in the inequality. So, either use $$.
We can then assign a point that is on the shaded region, say $(0,0)$ and determine what inequality to use:
$$
begin{align*}
y&=dfrac{1}{2}x-2\
0&stackrel{?}{=}dfrac{1}{2}(0)-2\
0&stackrel{?}{=}0-2\
0&stackrel{?}{=}-2
end{align*}
$$
The appropriate inequality to use is $>$ since $0> -2$. Hence, the inequality for the graph is:
$$
color{#c34632} y>dfrac{1}{2}x-2
$$
y>dfrac{1}{2}x-2
$$
$$
yle-3x+4 y>5x-2
$$
Substitute the value of $x=0$ for both inequalities as follows:
$$
yle0+4 yle4
$$
$$
y>0-2 y>-2
$$
Since the value of $y=4$ is the correct solution for both inequalities, so the point $(0, 4)$ is the correct solution for both inequalities.
text{color{#4257b2}$(0, 4)$ Correct solution}
$$
Triple of Audrey’s age, plus 9 is less than Lew’s age, which is 60. So, the inequality is:
$$
color{#c34632}3A+9<60
$$
Solve for $A$. Subtract 9 from both sides:
$$
3A<51
$$
Divide both sides by 3:
$$
A<17
$$
So, $text{color{#c34632}Audrey is less than 17 years old.}$
Assume the age of Audrey is $x$ years.
$$
3 x+9le60
$$
Isolate the variables on left side as follows:
$$
3xle60-9 3xle51
$$
Divide both of sides by $3$ as follows:
$$
xledfrac{51}{3} xle17
$$
The possible age for Audrey is $17$ years.
text{color{#4257b2}$17$ years}
$$
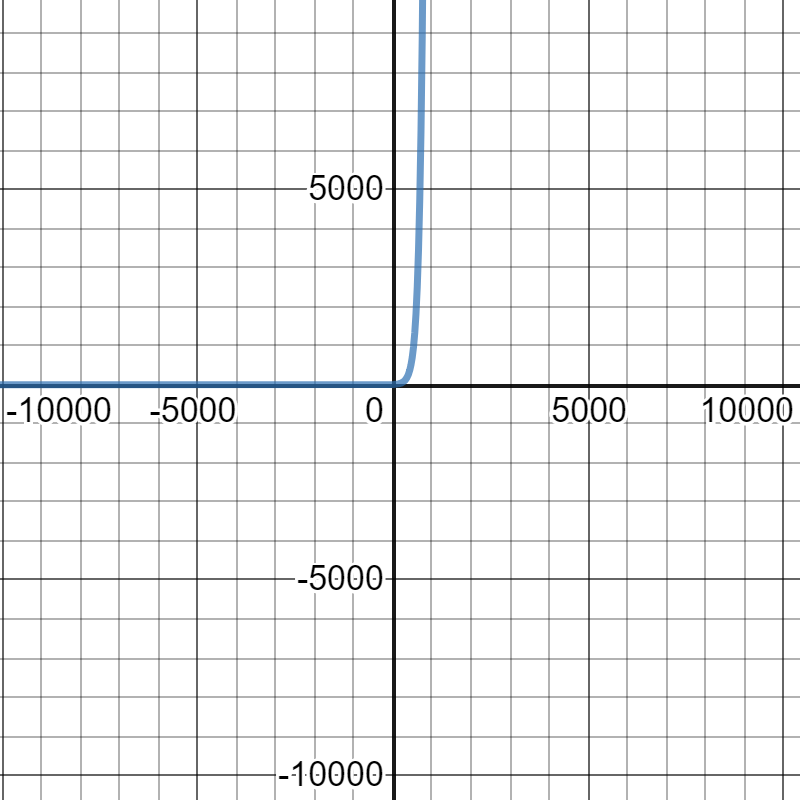
$$y=5(1.01)^x$$\
The following table is a table of values of the previous function:\
begin{center}
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$x$ & $y$ \
hline
$1$ & $5.05$ \
hline
$2$ & $5.1005$ \
hline
$3$ & $5.15$ \
hline
$4$ & $5.2$ \
hline
$5$ & $5.25$ \
hline
end{tabular}
end{center}
On the following picture, there is graph of previous equation.\
Let:
$$
begin{align}
2x-y&=9\
y&=x-7
end{align}
$$
Since $y$ is already isolated in eq. (2), use Substitution Method. Substitute eq. (2) to eq. (1) then solve for $x$:
$$
begin{align*}
2x-(x-7)&=9\
2x-x+7&=9\
x+7&=9\
x&=2
end{align*}
$$
Solve for $y$ using eq. (2):
$$
begin{align*}
y&=2-7\
y&=-5
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(2,-5)
$$
Let:
$$
begin{align}
-4x+y&=5\
2x&=-y-13
end{align}
$$
Using either of the two equations, we can isolate $y$. I chose eq. (1) to obtain the equation:
$$
y=4x+5tag{3}
$$
Use Substitution Method. Substitute eq. (3) to eq. (2) then solve for $x$:
$$
begin{align*}
2x&=-(4x+5)-13\
2x&=-4x-5-13\
2x&=-4x-18\
6x&=-18\
x&=-3
end{align*}
$$
Solve for $y$ using eq. (3):
$$
begin{align*}
y&=4(-3)+5\
y&=-12+5\
y&=-7
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(-3,-7)
$$
b. $(-3,-7)$
$$
color{#4257b2}text{(a)} (0, 2) text{and multiplier of} 0.8
$$
The exponent function form is $y=a b^x$. Substitution values of $(x, y)$ in the exponential form as follows:
$$
2=a b^0 2=a b=0.8
$$
$$
y=a b^x y=2cdot0.8^x
$$
$$
color{#4257b2}text{(b) passes through points} (0, 3.5) (2, 31.5)
$$
The exponent function form is $y=a b^x$. Substitution values of $(x, y)$ in the exponential form as follows:
$$
3.5=a b^0 3.5=a
$$
Substitution value of $a$ in the second equation as follows:
$$
31.5=3.5cdot b^2
$$
Divide both of sides by $3.5$ as follows:
$$
b^2=dfrac{31.5}{3.5} b^2=9
$$
Use square root property as follows:
$$
sqrt{b^2}=sqrt{9} b=3
$$
$$
y=a b^x y=3.5 (3)^x
$$
color{#4257b2}text{(c) passes through points} (3, 13.5) (5, 30.375)
$$
The exponent function form is $y=a b^x$. Substitution values of $(x, y)$ in the exponential form as follows:
$$
13.5=a b^3 a=dfrac{13.5}{b^3}
$$
Substitution value of $a$ in the second equation as follows:
$$
30.375=dfrac{13.5}{b^3}cdot b^5 30.375=13.5 b^2
$$
Divide both of sides by $13.5$ as follows:
$$
b^2=dfrac{30.375}{13.5} b^2=2.25
$$
$$
sqrt{b^2}=sqrt{2.25} b=1.5
$$
Substitution value of $b=1.5$ in the first equation as follows:
$$
a=dfrac{13.5}{b^3} a=dfrac{13.5}{1.5^3}
$$
$$
a=dfrac{13.5}{3.375} a=4
$$
$$
y=a b^x y=4 (1.5)^x
$$
text{color{#4257b2}(a) $y=2cdot0.8^x$ (b) $y=3.5cdot3^x$ (c) $y=4cdot1.5^x$}
$$
$$
color{#4257b2}text{(a)} 100, 10, 1, 0.1, ……
$$
$$
a_{0}=100
$$
$$
a_{1}=10=100cdot0.1=a_{0}cdot0.1
$$
$$
a_{2}=1=a_{1}cdot0.1=a_{0}cdot0.1cdot0.1 a_{2}=a_{0}cdot(0.1)2
$$
$$
color{#4257b2}a_{n}=100cdot(0.1)^n
$$
$$
color{#4257b2}text{(b)} 0, -50, -100, ……
$$
$$
a_{0}=0
$$
$$
a_{1}=-50=0-50=a_{0}-50
$$
$$
a_{2}=-100=a_{1}-50=a_{0}-50-50 a_{2}=a_{0}-(2cdot50)
$$
$$
color{#4257b2}a_{n}=-50 n
$$
text{color{#4257b2}(a) $a_{n}=100cdot(0.1)^n$ (b) $a_{n}=-50cdot n$}
$$
$because$ $angle PMQ=angle KML$
$because$ PM=LM
$because$ KM=QM
$therefore$ The two triangles are congruent
text{color{#4257b2}The two triangles are congruent}
$$
$$
color{#4257b2}text{(a)} |x|+3=8
$$
Equal $x+3=8$ as follows:
$$
x=8-3 x=5
$$
Equal $-x+3=8$ as follows:
$$
-x=8-3 -x=5 x=-5
$$
The values of $x$ are equal
$$
x=5 text{ when} xge0
$$
$$
x=-5 text{ when} x<0
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=5, x=-5$ in the equation as follows:
$$
|x|+3=8 |5|+3=8 5+3=8 8=8
$$
$$
|x|+3=8 |-5|+3=8 5+3=8 8=8
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(b)} |x-5|=17
$$
Equal $x-5=17$ as follows:
$$
x=17+5 x=22
$$
Equal $-x+5=17$ as follows:
$$
-x=17-5 -x=12 x=-12
$$
The values of $x$ are equal
$$
x=22 text{ when} x-5ge0 xge5
$$
$$
x=-12 text{ when} x-5<0 x<5
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=22, x=-12$ in the equation as follows:
$$
|x-5|=17 |22-5|=17 |17|=17 17=17
$$
$$
|x-5|=17 |-12-5|=17 |-17|=17 17=17
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}(a) $x=5$ or $x=-5$
\ \
(b) $x=22$ or $x=-12$}
$$
There you can see what are your problems in this chapter and try to work on that and make it better.

