
All Solutions
Page 365: Questions
Since the polygons are similar, the ratio of the corresponding sides shall be equal which is known as the scale factor.
By observation we see that
Polygon ABCDE $sim$ Polygon PLMNO
Since, $dfrac{MN}{CD} = dfrac{NO}{DE}$,
Therefore,
$$
begin{align*}
text{Scaling Factor} &=dfrac{10}{25} \
&= dfrac{14}{35} \
&= dfrac{2}{5} \
&= 0.4
end{align*}
$$
By property of similarity, we know that
$$
dfrac{PL}{AB} = dfrac{LM}{BC} =dfrac{OP}{EA}=0.4 text{(scaling factor)}
$$
$$
begin{align*}
dfrac{8}{z} &=dfrac{y}{25}\
&=dfrac{x}{17.5}\
&= 0.4\
end{align*}
$$
Therefore, the required values are,
$$
begin{align*}
z&= 8div 0.4 \
&= 20 \
y &= 25times0.4\
&= 10\
x &= 17.5times0.4 \
&= 7\
end{align*}
$$
Hence by the property of similarity of triangles we know that the ratio of the length of the similar sides are equal.
Therefore $dfrac{AB}{AD}=dfrac{BC}{DE}=dfrac{AC}{AE}$
After substituting the values respectively we get,
$dfrac{x+27}{x}=dfrac{28}{11.2}=dfrac{m+p}{m}$…….(1)
Therefore for solving for $x$ we get,
$$
begin{align*}
28x &=11.2x+302.4 \
x &= 18
end{align*}
$$
Now since $triangle ADE$ is a right angled triangle with hypotenuse as AE, we can apply the Pythagoras theorem,
$AD^{2}+DE^{2} = AE^{2}$
After substituting the values we get,
$$
begin{align*}
x^{2}+11.2^{2} &= AE^{2}\
AE =m &= 21.2
end{align*}
$$
Substituting value pf $m$ in equation (1) we get,
$$
dfrac{28}{11.2}=dfrac{21.2+p}{p}
$$
After solving for $p$ we get,
$$
28times11.2=11.2p+237.44
$$
$$
p=6.8
$$
The following polygons appear to be congruent:
1. Polygon B and Polygon D
2. Polygon L and Polygon G
3. Polygon E and Polygon H
Following are the sequence of rigid transformations that would demonstrate the congruence between the above mentioned polygons:
1. Clockwise rotation of polygon B
2. Translation upwards and anticlockwise rotation of polygon L
3. Reflection of polygon H
The corresponding angle measures and the corresponding sides of congruent polygons shall be equal.
According to the definition, congruent polygons need to have same number of sides and all corresponding sides and angles are equal and also the polygons shall have same shape and size for which one may be rotated or made a mirror image of.
Hence the corresponding side and angles shall be equal.
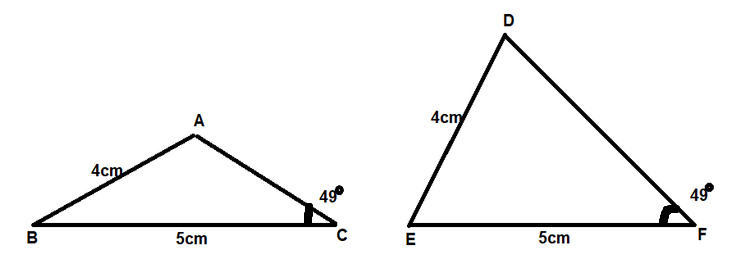
Since $triangle ABC$ is a right-angled triangle at $angle A$, we can apply the Pythagoras theorem.
$AB^{2}+BC^{2}=AC^{2}$
After substituting the values we get,
$$
63^{2}+16^{2}=AC^{2}
$$
Hence $AE=65$.
Similarly $triangle DEF$ is a right-angled triangle at $angle E$, we can apply the Pythagoras theorem.
$$
DE^{2}+EF^{2}=DF^{2}
$$
After substituting the values we get,
$$
DE^{2}+16^{2}=65^{2}
$$
Hence $DE=63$.
By observation we can see that
$AB=DE; BC=EF; AC=DF$
Hence $triangle ABC cong triangle DEF$ by SSS test of congruency.
The triangle on right can be mapped on the triangle on right by two rigid transformations which are as follows:
1. 90 degrees of Clockwise rotation
2. Translation towards right
$triangle MNP cong triangle UWV$
Here we can observe that
$MN = UW = 20 cm$
$$
NP = WV = 16cm
$$
$$
MP = UV = 8cm
$$
So by using SSS test of ongruence we can say that $triangle MNP cong triangle UWV$
Let us first make a mirror image of $triangle MNP$ with mirror along side MN. Now perform lateral translation of $triangle MNP$ towards right and we can have them map on each other.
$triangle ABC cong triangle DEF$
We know that $triangle ABC$ is a right-angled triangle at $angle A$, thus we can apply the Pythagoras theorem.
Accotding to the pythagorus theorem:
$$
AB^{2}+BC^{2}=AC^{2}
$$
After substituting the values we get,
$$
63^{2}+16^{2}=AC^{2}
$$
$AE=65$ …..(1)
Similarly $triangle DEF$ is a right-angled triangle at $angle E$, thus even here we can apply the Pythagoras theorem.
$$
DE^{2}+EF^{2}=DF^{2}
$$
After substituting the values we get,
$$
DE^{2}+16^{2}=65^{2}
$$
$DE=63$…..(2)
By observation we can see that
$AB=DE; BC=EF; AC=DF$
Hence $triangle ABC cong triangle DEF$ by SSS test of congruency.
$UV = XZ = 110$
$UW = XY = 280$
$VW = ZY = 240$
Hence we can conclude that $triangle UVW cong triangle XZY$ by SSS test of congruency.
1. Clockwise rotation of $triangle UVW$ such that side $VW$ is on the base. We should get a triangle similar to the one on the left.
2. Mirror image of the $triangle UVW$ with a vertical mirror.
3. Translation of the triangle on top of the triangle on right.
triangle UVW cong triangle XZY
$$
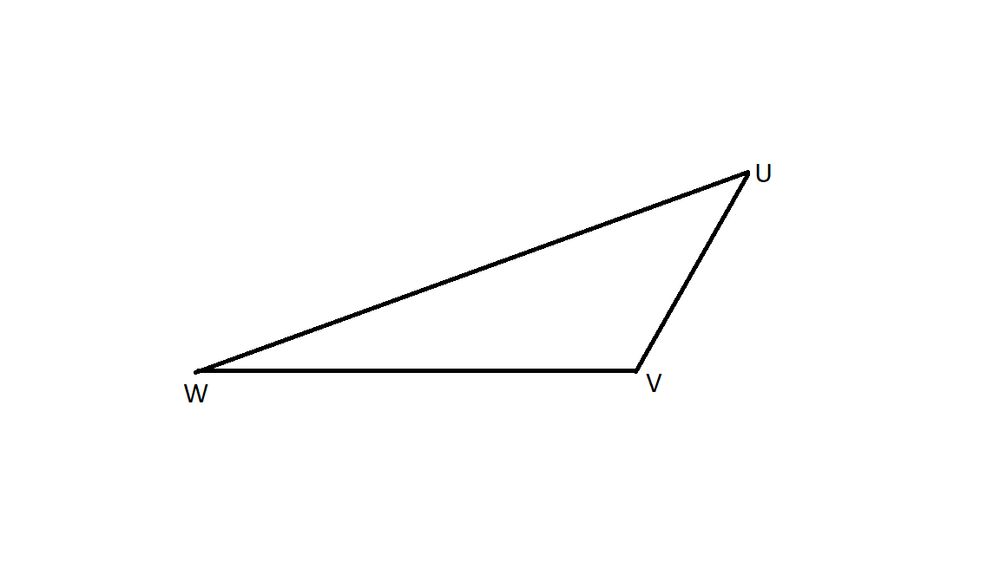
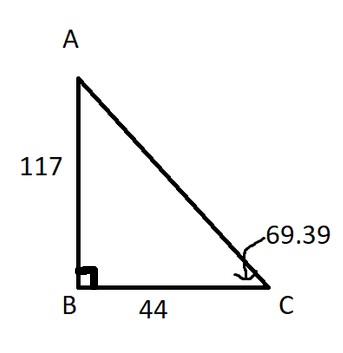
We can see that $triangle ABC$ is right angled on $angle B$.
By the property of triangle we know that,
$$
angle A + angle B + angle C = 180^{0}
$$
After substitution we get $angle A = 20.61$
Also we can apply the Pythagoras theorem on $triangle ABC$, we get
$$
AB^{2}+BC^{2}=AC^{2}
$$
After substitution of values we get, $AC = 125$.
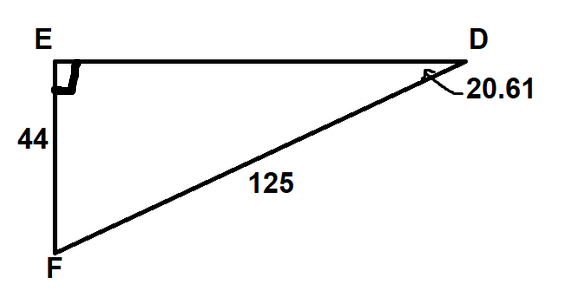
By the property of triangle we know that,
$$
angle D + angle E + angle F = 180^{0}
$$
After substitution we get $angle F = 69.39^{0}$
Also we can apply the Pythagoras theorem on $triangle ABC$, we get
$$
DE^{2}+EF^{2}=DF^{2}
$$
After substitution of values we get, $DE = 117$
Hence we can say that $triangle ABC cong triangle DEF$ by SSS test of congruency.
angle A= 20.61
$$
$$
angle F = 69.39
$$
$$
AC = 125
$$
$$
DE = 117
$$
$triangle ABC cong triangle DEF$ by SSS test of congruency.
$textbf{(a)}$ Scale factor is defined as the ratio of the side length of the new figure to the similar side length of the old figure.
$Rightarrow$
$$
text{Scale factor}=dfrac{text{PQ}}{text{AB}}=dfrac{10}{4}=2.5
$$
Therefore, the scale factor is 2.5
$textbf{(b)}$ The scaling factor will be the same for any two similar sides. The side AD is similar to the side PS.
$Rightarrow$
$$
begin{align*}
dfrac{text{PS}}{text{AD}}&=2.5\
dfrac{x}{7}&=2.5tag{multiply each side by 7}\
dfrac{x}{7}cdot 7&=2.5cdot 7\
x&=17.5
end{align*}
$$
As all the sides are in mm, therefore, the value of $x$ will be 17.5 mm.
$textbf{(b)}$ 17.5 mm
Let point A $= (x_1,y_1) = (-4,0)$
Let point B $= (x_2,y_2) = (0,9)$
Slope of the line $= m = dfrac{y_2-y_1}{x_2-x_1}$
Hence, slope of the line $= m = dfrac{9-0}{0-(-4)} = dfrac{9}{4}$
$y-y_1=m(x-x_1)$
$y-0 = dfrac{9}{4} (x + 4)$
$4y=9x+36$
Therefore, $9x – 4y + 36 = 0$
textbf{(a)} The given sequence cannot be arithmetic as the difference between every consecutive term is not constant here.\
Every next term of this sequence can be obtained by multiplying the previous term by $dfrac{1}{2}$ and hence this is a geometric sequence with the common ratio equal to $r=dfrac{t(n+1)}{t(n)}=dfrac{1}{2}$\\
textbf{(b)} For graphing the sequence we need to find $t(5)$ and $t(6)$. $t(5)$ can be obtained by multiplying $t(4)$ by $dfrac{1}{2}$ and similarly, $t(6)$ can be obtained by multiplying $t(5)$ by $dfrac{1}{2}$\
$Rightarrow$
begin{align*}
t(5)&=dfrac{1}{2}cdot t(4)=dfrac{1}{2}cdot 5=2.5\
t(6)&=dfrac{1}{2}cdot t(5)=dfrac{1}{2}cdot 2.5=1.25
end{align*}
Therefore, we have mentioned set of points to locate on the graph and draw a curve through them.
begin{center}
begin{tabular}{|p{1cm}|p{1cm}|}
hline
x&y\
hline
1&40\
hline
2&20\
hline
3&10\
hline
4&5\
hline
5&2.5\
hline
6&1.25\
hline
end{tabular}
end{center}
$$
t(n)=40(dfrac{1}{2})^{n-1}
$$
From the explicit equation, we can see that the lowest value this sequence can obtain is close to 0 when the value of $n$ will tend to infinity. Therefore, the values of the sequence will never become negative or zero (not exact as $n$ infinity can never be achieved). Although an approximate zero value can be obtained when the term number $(n)$ tends to infinity.
$textbf{(b)}$ Exponential function (discrete valued)
$textbf{(c)}$ No, sequence can never attain zero (exact) or negative values. Although an approximate zero value can be obtained when the term number $(n)$ tends to infinity.
We have given pair of equations as
$$
begin{align}
y&=3x\
2y&-5x=4
end{align}
$$
This pair of equation can be solved by substitution method. On putting $y=3x$ into the equation (2), it will result in an equation of single variable in terms of $x$ only.
$$
begin{align*}
2y-5x&=4\
2(3x)-5x&=4\
6x-5x&=4\
x&=4
end{align*}
$$
We can solve for $y$ by putting $x=4$ into $y=3x$, which gives
$$
y=3cdot(4)=12
$$
Therefore , the solution point is $(4,12)$.
We have given pair of equations as
$$
begin{align}
x-4&=y\
-12=&3y-3x
end{align}
$$
This pair of equation can be solved by substitution method. On putting $y=x-4$ into the equation (2), it will result in an equation of single variable in terms of $x$ only.
$$
begin{align*}
-12&=3y-3x\
-12&=3(x-4)-3x\
-12&=3x-12-3x\
-12&=-12tag{true always}
end{align*}
$$
Therefore, the given system is true for any values of $x$ and $y$. hence, this system has infinite number of solutions. In fact, equation (2) can be obtained by multiplying the equation (1) by 3 and then rearrangment. Therefore, these are the same equations.
$textbf{(b)}$ Infinite number of solutions.
Let us look at $triangle NMP$.
Since the triangle is right-angled triangle at $angle M$, we can apply the pythagoras theorem.
$NM^{2}+MP^{2}=NP^{2}$
After substituting the values we get, $MP =21$
Since we know that sum of all interior angles of a triangle is 180 degrees, that is $angle N + angle M +angle P = 180^{0}$
Hence $angle N = 36.87^{o}$
Let us now look at $triangle QRS$.
Since the triangle is right-angled triangle at $angle Q$, we can apply the pythagoras theorem.
$RQ^{2}+QS^{2}=RS^{2}$
After substituting the values we get, $QS =28$
Since we know that sum of all interior angles of a triangle is 180 degrees, that is $angle Q + angle R +angle S = 180^{0}$
Hence $angle R = 53.13^{o}$
We can say that the triangles are congruent by SSS test of congruency
No Jovan is not correct, there is always a certain set of rigid transformations which would make one triangle map onto other if the triangles are congruent.
It isn’t possible to have equal measures of angles and equal side lengths and even then the triangles are not congruent.
Yes Mia is right.
If two segments have equal length, they must be congruent. There is always a sequence of rigid transformations that maps one segment onto the other. We saw in the earlier 7.12 a how each sides are equal.
$angle N cong angle S$
$angle M cong angle Q$
$angle P cong angle R$
$overline{MN} cong overline{QS}$
$overline{NP} cong overline{SR}$
$overline{MP} cong overline{QR}$
No I do not think that 2 triangles must be congruent if all three pairs of corresponding angles are congruent. They will be similar triangles but not necessarily congruent.
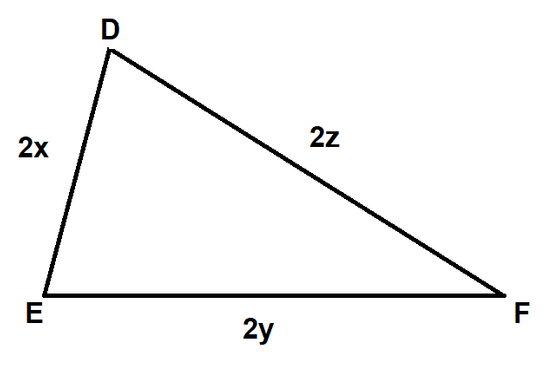
$angle A = angle D = 62^{o}$
$angle B = angle E = 80^{o}$
$angle C = angle F = 38^{o}$
Thus we can say $triangle ABC sim triangle DEF$ by AAA test of similarity.
The two triangles are not congruent since their side lengths are not equal.
$dfrac{DE}{AB} = dfrac{EF}{BC} = dfrac{DF}{AC} = 2 = scaling factor$
Thus this shows that if we keep changing the scaling factor then we can have numerous triangles which are similar to $triangle ABC$ but aren’t congruent to it.
No Jovan’s method of comparing just the angle measures isn’t the correct way to state if the triangles are congruent. One must also check if the corresponding side lengths are equal as well along with the corresponding angles.
If we know that all three pairs of corresponding angle measures are congruent and also one pair of corresponding side is equal then the triangles also willl be congruent.
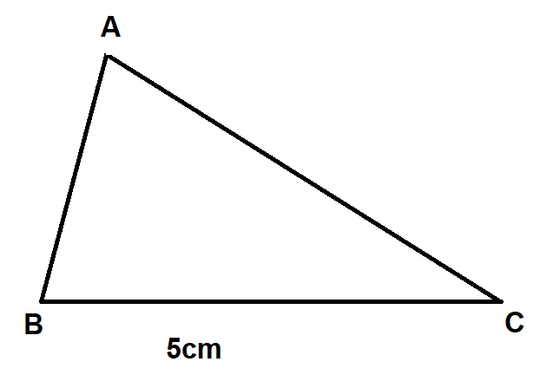

$angle A = angle D = 62^{o}$
$angle B = angle E = 80^{o}$
$angle C = angle F = 38^{o}$
$BC = EF = 5$ cm
Since all the three angles are equal we know that $triangle ABC sim triangle DEF$.
We know that for similar triangles the ratio of their corresponding sides is equal to the scaling factor.
$dfrac{AB}{DE} = dfrac{BC}{EF} = dfrac{5}{5} = dfrac{AC}{DF} = 1$
Now since the scaling factor is equal to 1, the corresponding sides of both triangles is equal.
Hence we can conclude that $triangle ABC cong triangle DEF$
It is $textbf{NOT}$ possible to make a pair of triangles with the three given corresponding angle measures, and one equal corresponding side length, that are not congruent
Yes Jovan’s method to compare three pairs of corresponding angles and 1 pair of corresponding side is a good method of identifying if the triangles are congruent or not
For the above drawn triangles, the rigid transformations that we would perform are a clockwise rotation of $triangle DEF$ and then followed by lateral translation towards left, to map it on the $triangle ABC$.
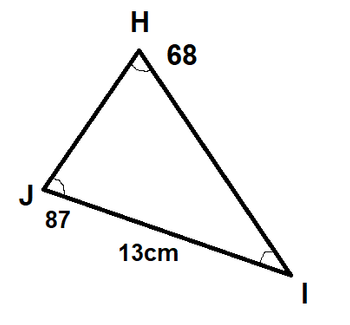
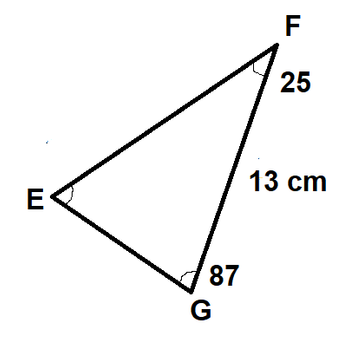
$measuredangle H = 68^{o}$
$measuredangle F = 25^{o}$
$measuredangle J = measuredangle G = 87^{o}$
$$
IJ = FG = 13cm
$$
For the triangle on the left we know that
$measuredangle H = 68^{o}$; $measuredangle J = 87^{o}$ Thus $measuredangle I = 25^{o}$
For triangle on the right we know that
$measuredangle F = 25^{o}; measuredangle G = 87^{o}$ Thus $measuredangle E = 68^{o}$
Since all three pairs of corresponding angles are congruent, the $triangle HJI sim triangle EGF$
For similar triangles,
$dfrac{HJ}{EG}=dfrac{JI}{GF}=dfrac{13}{13}=dfrac{HI}{EF}= 1 =$ scaling factor
Thus all the three pair of corresponding sides are equal.
Hence $triangle HJI cong triangle EGF$
2 pairs of corresponding angles need to be equal to make sure that the triangles are congruent.
The minimum amount of information required to determine that 2 triangles are congruent are as follows:
1. 2 pairs of corresponding angles
2. 1 pair of corresponding sides
By knowing that 2 angles are congruent we know that the third angle is also congruent since sum of 3 angles of a triangle is $180^{o}$.
Hence having 3 pairs of angles congruent makes the triangle similar. For similar triangles, we know that the ratio of corresponding sides is a constant which is equal to the scale factor.
By an additional information that one corresponding side is congruent, we know that the scaling factor is 1.
Thus all sides are congruent.
Hence we can say the triangles are congruent.
b$triangle RDC cong triangle WBY$; It is congruent by AAS $cong$; mirror image of $triangle RDC$ along side $CD$ will map the triangle on the $triangle WBY$
c.$triangle ABC cong triangle ZXY$: It is congruent by AAS$cong$ and ASA$cong$; Anticlockwise rotation of $triangle ZYX$ will map the triangle on $triangle ABC$
d.$triangle ABC cong triangle CDA$; It is congruent by AAS$cong$ and ASA$cong$; Taking a mirror image of $triangle ADC$ along the side $AC$ followed by another mirror image with mirror $bot$ to side $AC$.
1. How to identify if triangles are similar.
2. SSS, ASA, AAS test of congruency.
3. We just need a minimum of 2 pair of corresponding angles and 1 pair of corresponding side to determine if the pair of triangles are congruent.
First, we need to give the name to the vertices so that we can easily name the side we are talking. The labeled diagram is attached below.
$$
Rightarrow
$$
It is given that the polygons are similar, therefore each similar sides will be scaled with the same factor.
$$
begin{align*}
text{Scaling factor}&=dfrac{text{PQ}}{text{AB}}=dfrac{text{QR}}{text{BC}}=dfrac{text{QS}}{text{CD}}=dfrac{text{SP}}{text{DA}}\
text{Scaling factor}&=dfrac{4}{6}=dfrac{y}{12}=dfrac{6}{x}=dfrac{z}{5.7}
end{align*}
$$
The scaling factor is $dfrac{4}{6}=0.667$. Using the ratio from the above equation, we can calculate the length of the missing sides in parts.
$bullet$ Solving for $y$.
$$
begin{align*}
dfrac{4}{6}&=dfrac{y}{12}tag{multiply each side by 12}\
dfrac{4}{6}cdot 12&=dfrac{y}{12}cdot 12\
4cdot 2&=y\
y&=8 text{ ft}
end{align*}
$$
$$
begin{align*}
dfrac{6}{x}&=dfrac{4}{6} tag{multiply each side by $6x$}\
dfrac{6}{x} cdot 6x&=dfrac{4}{6}cdot 6x\
6cdot 6&=4cdot x\
36&=4xtag{ divide each side by $4$}\
dfrac{36}{4}&=dfrac{4x}{4}\
9&=x\
x&=9 text{ ft}
end{align*}
$$
$bullet$ Solving for $z$.
$$
begin{align*}
dfrac{z}{5.7}&=dfrac{4}{6}tag{multiply each side by 5.7}\
dfrac{z}{5.7} cdot 5.7&=dfrac{2}{3}cdot 5.7 \
z&=3.8 text{ ft}
end{align*}
$$
$x$ $rightarrow$ 9 ft
$y$ $rightarrow$ 8 ft
$z$ $rightarrow$ 3.8 ft
Side NA $=$ side EO
Side AH $=$ side OJ
Side NH $=$ side EJ
Therefore, $Delta text{NAH} cong Delta text{EOJ}$ by SSS $cong$.
A vertical reflection by a line passing through the middle of the figures, will map them onto each other.
A vertical reflection by a line passing through the middle of the figures, will map them onto each other.
$$
begin{align}
y&=-dfrac{2}{5}x+1\
y&=-dfrac{2}{5}x-2
end{align}
$$
We can try to solve the given system by using the Substitution method.Substitute $y=-dfrac{2}{5}x+1$ into the equation $(2)$. This will result in an equation of a single variable in terms of $x$ and we will try to solve that.
$$
begin{align*}
y&=-dfrac{2}{5}x-2\
(-dfrac{2}{5}x+1)&=-dfrac{2}{5}x-2tag{ add $dfrac{2}{5}x $ to the each side}\
-dfrac{2}{5}x+dfrac{2}{5}x+1&=-dfrac{2}{5}x+dfrac{2}{5}x-2\
1&=-2tag{not true}
end{align*}
$$
We can see that we have got a mathematically false equation, while trying to solve for the system. Therefore, the given system has no solution.
In fact, on comparing the equations given in the system with $y=mx+c$ where $m$ represents the slope of the line and $c$ represents the $y$-intercept, We can see that the slopes of the given two equations are the same by the $y$-intercepts are different. This means that the given lines are parallel to the each other with no point of intersection at any point.
In fact, on comparing the equations given in the system with $y=mx+c$ where $m$ represents the slope of the line and $c$ represents the $y$-intercept, We can see that the slopes of the given two equations are the same but the $y$-intercepts are different. This means that the given lines are parallel to the each other with no point of intersection at any point.
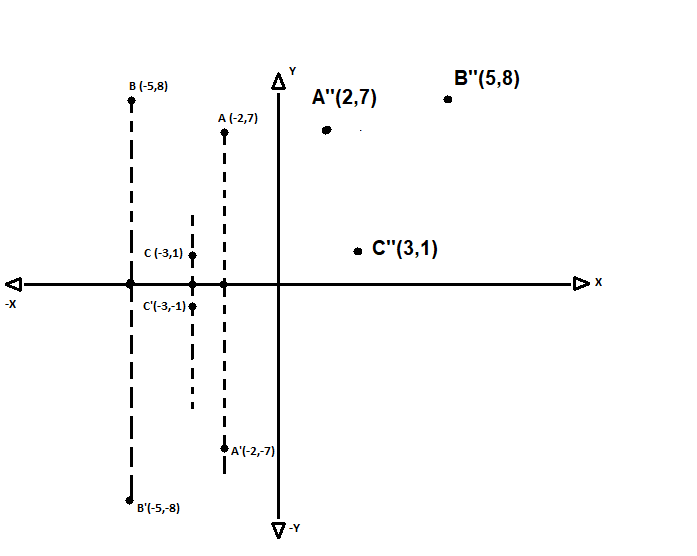
We know that vertices of $triangle ABC$ are $A(-2,7); B(-5,8); C(-3,1)$
When we reflect these vertices about the X-axis, that means the midpoint of the old vertice and the new vertice should lie on the X-axis.
Hence the Y coordinate of the midpoint should be zero.
Hence the new vertices are $A'(-2,-7); B'(-5,-8); C'(-3,-1)$.
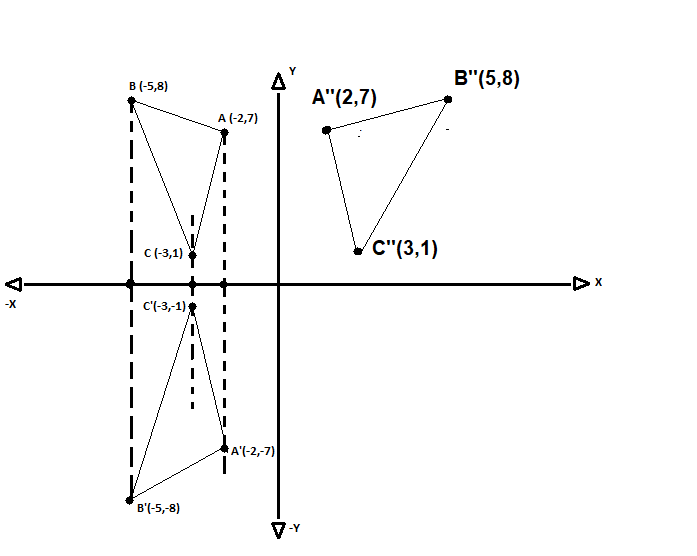
When we rotate the vertice about the origin that is by an angle of $180^{o}$, both the x-coordinate and the y-coordinate are negated (their signs are changed). In a point reflection in the origin, the image of the point (x,y) is the point (-x,-y).
Thus after taking reflections of $A’;B’;C’$ in the origin, we have our new vertices $A”(2,7); B”(5,8), C”(3,1)$.
To get the $triangle ABC$ to be mapped on $triangle A”B”C”$ by a single transformation, we shall need to perform reflection of the vertices of $triangle ABC$ about the Y-axis.
Now that it is given that Nina has some nickels and 9 pennies. Her friend Maurice has twice as many nickels as Nina. Let $x$ represents the number of nickels that Nina has, and $y$ represents the number of nickels of Maurice. So the equation for this situation is
$$
y=2x
$$
Given that their coins are worth 84textcent. so the equation for this situation can be written by multiplying the number of coins (variables) by its worth in cents.
$$
(x+y)cdot 5+9cdot 1=84
$$
We have the system of the equation to solve as
$$
begin{align*}
y&=2x\
5x&+5y+9=84
end{align*}
$$
We can solve this system by using the Substitution method. Substitute the value of $y$ form the first equation into the second equation and solve for $x$.
$$
begin{align*}
5x+5y+9&=84\
5x+5(2x)+9&=84\
5x+10x&=84-9\
15x&=75tag{ divide each side by $15 $}\
dfrac{15x}{15}&=dfrac{75}{15}\
x&=5
end{align*}
$$
Put $x=5$ into $y=2x$ and solve for $y$.
$$
begin{align*}
y&=2x\
y&=2(5)\
y&=10
end{align*}
$$
Therefore, Nina has 5 nickels and 9 pennies and Maurice has 10 nickels.
$textbf{(a)}$ The inputs and outputs of this function are discrete as it takes only integral inputs and outputs.
Domain $rightarrow$ ${0,1,2}$
Range $rightarrow$ ${-2,0,1}$
$textbf{(b)}$ $x$ is varying from $-1$ to $+1$ and $y$ is varying from $-1$ to $2$. Therefore,
Domain $rightarrow$ $[-1,1]$
Range $rightarrow$ $[-1,2]$
$textbf{(c)}$ $x$ is varying from $-infty$ to $+2$ and $y$ is varying from $-2$ to $+infty$. Therefore,
Domain $rightarrow$ $(-infty,2]$
Range $rightarrow$ $[-2,+infty)$
$textbf{(d)}$ $x$ is varying from $-infty$ to $+infty$ and $y$ is varying from $-1$ to $+infty$ . Therefore,
Domain $rightarrow$ $(-infty,+infty)$
Range $rightarrow$ $[-1,+infty)$
Range $rightarrow$ ${-2,0,1}$
$textbf{(b)}$ Domain $rightarrow$ $[-1,1]$
Range $rightarrow$ $[-1,2]$
$textbf{(c)}$ Domain $rightarrow$ $(-infty,2]$
Range $rightarrow$ $[-2,+infty)$
$textbf{(d)}$ Domain $rightarrow$ $(-infty,+infty)$
Range $rightarrow$ $[-1,+infty)$
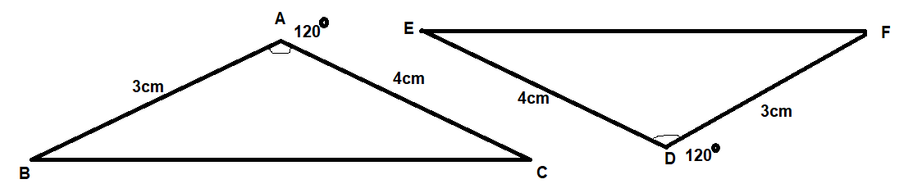
$mangle B=mangle F$ but $mangle C ne mangle E$
Therefore, the given triangles are not congruent. Although these have all the angle pairs similar but, these are not the in the required manner. Having all same angles will only give the guarantee of similarities between the two. For congruence, they should be following SSS, SAS, ASA, AAS or RHS$cong$. but the above case is not following any of these.
$$
bullet
$$
$$
begin{align*}
180text{textdegree}-(90text{textdegree}+55text{textdegree})&=35text{textdegree}
end{align*}
$$
$$
bullet
$$
$$
begin{align*}
180text{textdegree}-(90text{textdegree}+35text{textdegree})&=55text{textdegree}
end{align*}
$$
So, we got that all the three angles of the triangle are equal to each other. But we have no information available for the side length. AAA rule is not sufficient condition for congruence. For congruence, information about equality of at least one side should be there, along with the AAA condition. Without this information, we can only say that the given triangles are similar but we cannot comment about congruence.
If these were congruent triangles, then we could map one triangle onto the other by performing reflection along the hypotenuse followed by a rotation.
$$
begin{align}
6x-2y&=10\
3x-2&=y
end{align}
$$
we can solve this system using Substitution method. Substitute the $y=3x-2$ into the equation $(1)$ and solve for $x$.
$$
begin{align*}
6x-2y&=10\
6x-2(3x-2)&=10\
6x-6x+4&=10\
4&=10tag{not true}
end{align*}
$$
All the $x$ terms got cancelled and we got a non-true equatlity. Therefore, this system of the equations have no solutions.
$$
textbf{(b)}
$$
$$
begin{align*}
3x-9y&=3\
2x&=16-y
end{align*}
$$
We can rearrange $2x=16-y$ to write $-2x+16=y$, so now we can substitute the $y$ equal to $-2x+16$ into the equation $3x-9y=3$, and solve for $x$.
$$
begin{align*}
3x-9y&=3\
3x-9(-2x+16)&=3\
3x+18x-144&=3tag{ add $ 144$ to the each side}\
21x&=147tag{ divide each side by $21$}\
dfrac{21x}{21}&=dfrac{147}{21}\
x&=7
end{align*}
$$
put $x=7$ into $-2x+16=y$ and solve for $y$.
$$
begin{align*}
-2x+16&=y\
-2(7)+16&=y\
-14+16&=y\
2&=y
end{align*}
$$
The solution point is $(7,2)$
$$
begin{align}
y&=3x+1\
x&+2y=-5
end{align}
$$
substitute $y=3x+1$ into the equation (2) and solve for $x$.
$$
begin{align*}
x+2y&=-5\
x+2(3x+1)&=-5\
x+6x+2&=-5tag{subtract $2 $ from the each side}\
7x+2-2&=-5-2\
7x&=-7tag{ divide each side by $7$}\
x&=-1
end{align*}
$$
Put $x=-1$ into the equation $(1)$ and solve for $y$.
$$
begin{align*}
y&=3x+1\
y&=3(-1)+1\
y&=-3+1\
y&=-2
end{align*}
$$
The solution point is $(-1,-2)$
textbf{(d)}
$$
$$
begin{align}
2x+3y&=9\
x-2y&=1
end{align}
$$
We can rearrange $x-2y=1$ to write $x=2y+1$, so now we can substitute the $x$ equal to $2y+1$ into the equation $(1)$, and solve for $y$.
$$
begin{align*}
2x+3y&=9\
2(2y+1)+3y&=9\
4y+2+3y&=9tag{subtract $2 $ from the each side}\
7y+2-2&=9-2\
7y&=7tag{ divide each side by $7$}\
y&=1
end{align*}
$$
put $y=1$ into $x=2y+1$ and solve for $x$.
$$
begin{align*}
x&=2y+1\
x&=2(1)+1\
x&=2+1\
x&=3
end{align*}
$$
The solution point is $(3,1)$
$textbf{(b)}$ The solution point is $(7,2)$.
$textbf{(c)}$The solution point is $(-1,-2)$
$textbf{(d)}$ The solution point is $(3,1)$
$$
text{rebound ratio}=dfrac{text{final height}}{text{Initial drop height}}=dfrac{120}{160}=dfrac{3}{4}=0.75
$$
$textbf{(a)}$ Height after $2^text{nd}$ bounce.
$$
begin{align*}
text{height}_2&=160times 0.75times 0.75\
&=160times (0.75)^2\
&=160times 0.5625\
&=90 text{ cm}
end{align*}
$$
$textbf{(b)}$ Height after $5^text{th}$ bounce.
$$
begin{align*}
text{height}_5&=160times 0.75times 0.75times 0.75times 0.75times 0.75\
&=160times (0.75)^5\
&=160times 0.2373\
&=37.968\
&approx38 text{ cm}
end{align*}
$$
$textbf{(c)}$ Height after $n^text{th}$ bounce.
$$
begin{align*}
text{height}_n&=160times (0.75)^n
end{align*}
$$
$textbf{(b)}$ 38 cm
$textbf{(c)}$ $text{height}_n=160times (0.75)^n$
Rebound ratio = 0.75
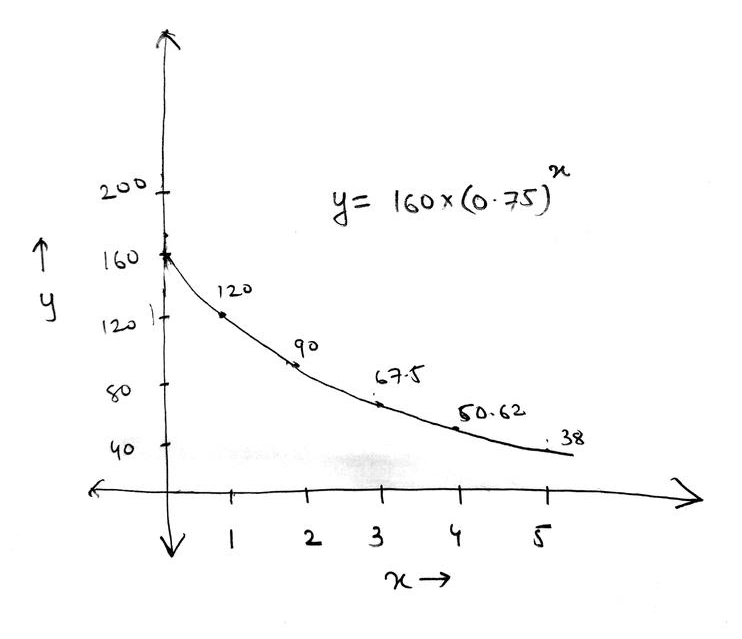
This problem is a typical problem of a geometric progression with
$a_1 = 160$; $a_2 = 120$; $a_3 = 90$; $a_4 = 67.5$ etc
Thus we can make a graph such that
$y=160 times 0.75^{x}$, ( $x$ takes positive numbers)
We shall get a graph like the one in the right.
Here $y$ stands for the height of the bounce and value of $x$ stands for the number of bounces.
We can find the time to travel 325 miles with a total speed of 125 miles per hour by using the formula.
$$
begin{align*}
text{Time}&=dfrac{text{Distance}}{text{Speed}}\
&=dfrac{325}{125} left ( dfrac{text{miles}}{text{miles}/text{hour}} right)\
&=2.6 text{ hours}
end{align*}
$$
We know that 1 hour has 60 minutes, therefore, $0.6$ hours will we equivalent to $0.6times 60=36$ minutes.
Therefore, It will take 2 hours and 36 minutes for Esther and Agnes to meet each other.
Yes $triangle ABC cong triangle TPO$
We can see that
$measuredangle A cong measuredangle T$;
$measuredangle B cong measuredangle P$;
$AC cong TO$
Thus we have 2 pairs of corresponding angles congruent and one pair od side length congruent.
Hence the 2 pair of triangles are congruent by $AAScong$.
Our method of solving is analogous to that of Julio’s. We used the given data whereas Julio made a flowchart for the solution. A flowchart helps us better to visualize. the problem at hand.
He used the same reasoning to determine if the pairs of triangles are congruent.
by AAS test.
Since the 2 pair of triangles are congruent, the corresponding side lengths shall be equal.
It is given that $overline{CT} = 15$; thus $overline{PI}=15$
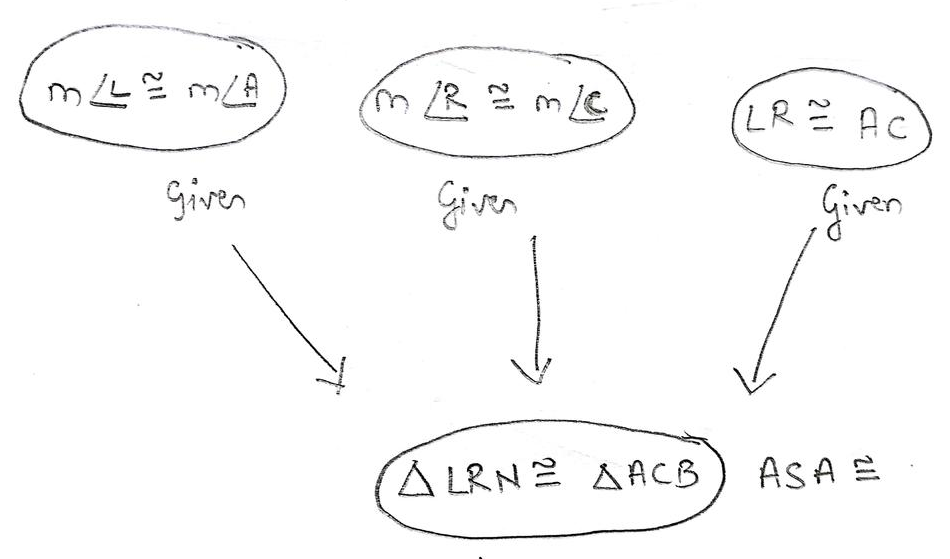
To make the 2 pairs of triangles congruent by ASA$cong$, Ramon would be using
1. $measuredangle L cong measuredangle A$
2. $measuredangle R cong measuredangle C$
Check detailed solution inside.
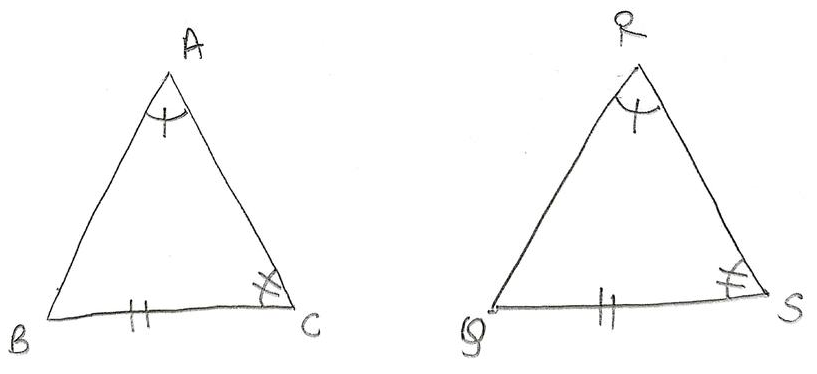
In Marcy’s flowchart, it is stated already that the 2 pairs of triangles are congruent by AAS $cong$.
Later she identifies which are the two congruent pair of angles and one congruent pair of sides.
Whereas in Lindsay’s problem, she was identifying how are the pair of triangles congruent given that we know the two pairs of angles and one pairs of sides as congruent.
Basically, the two given statements are different in both cases.
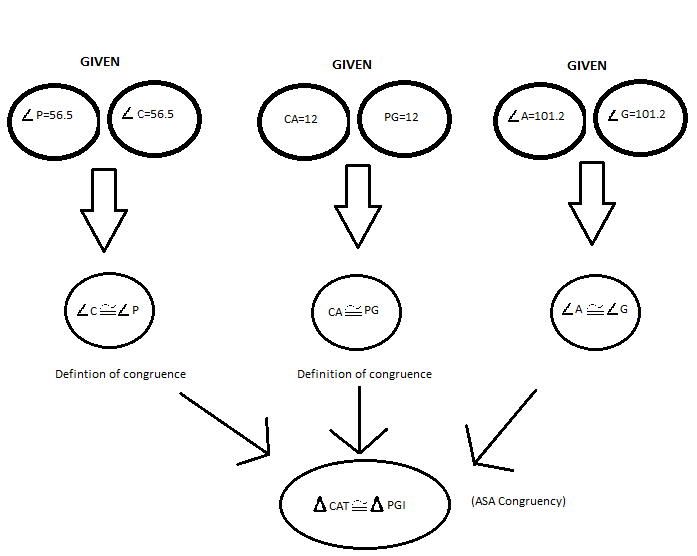
If we look at the question 7-32, we made this flowchart as we can see in the right.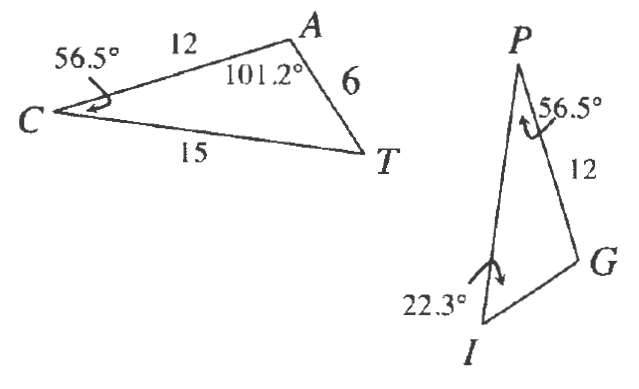

The reasins besides the ovals are decided by what we are trying to mention in the oval, for example if we mention a given statement, we need to write Given and if we mention a congruency statement, we need to mention the reason for it.
Examining $triangle ABC$
$measuredangle B = 25^{0}; measuredangle C = 39^{0}$; hence $measuredangle A = 116^{0}$ (sum of all angles of a triangle is $180^{o}$.
After examinig $triangle DEF$, we see the following on the right
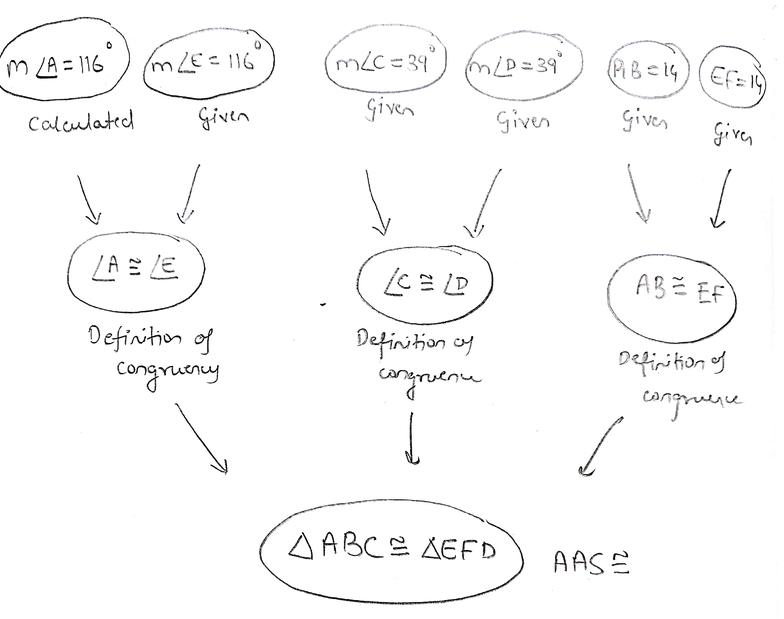
We know that the triangles are congruent. Hence the pair of corresponding angles must be equal.
Hence $DF = 20’$
$$
begin{align*}
text{Scaling ratio}&=dfrac{text{new side length}}{text{original side length}}\
&=dfrac{8}{18}\
&=0.4445
end{align*}
$$
In the similar triangles, all the sides grow in the same proportion of the scaling ratio. To find the value of $x$ we need to multiply the similar side of bigger triangle (length 8 ) with the scaling ratio.
$$
Rightarrow
$$
$$
begin{align*}
x&=0.4445times 8\
x&=3.556
end{align*}
$$
$$
begin{align}
2x+2y&=18\
x=3&-y
end{align}
$$
We can solve this system using Substitution method. Substitute the value of variable $x$ from the equation (2) into the equation (1) and solve for $y$ in the resultant equation.
$$
begin{align*}
2x+2y&=18\
2(3-y)+2y&=18\
6-2y+2y&=18\
6&=18tag{not true}
end{align*}
$$
The variable $x$ gets cancelled and we get an equality which is not true. Therefore, the given system has no solution. In fact the given lines are parallel to each other with the same slope and different $y$-intercepts.
textbf{(b)}
$$
$$
begin{align}
c&=-b-11\
3c&+6=6b
end{align}
$$
substitute the value of $c$ from the equation (1) into the equation (2) and solve for $b$.
$$
begin{align*}
3c+6&=6b\
3(-b-11)+6&=6b\
-3b-33+6&=6btag{ add $3b$ to the each side}\
-3b+3b-27&=6b+3b\
-27&=9btag{ divide each side by $9$}\
dfrac{-27}{9}&=dfrac{9b}{9}\
-3&=b
end{align*}
$$
put $b=-3$ into the equation $c=-b-11$ and solve for $c$.
$$
begin{align*}
c&=-b-11\
c&=-(-3)-11\
c&=+3-11\
c&=-8
end{align*}
$$
Therefore, the solution point is $(b,c)=(-3,-8)$
$textbf{(b)}$ The solution point is $(b,c)=(-3,-8)$
$$
begin{align*}
& dfrac{1.32times 10^5}{2times 10^{-3}}\
&=left (dfrac{1.32}{2} right)times left ( dfrac{10^5}{10^{-3}} right) tag{use $dfrac{a^m}{a^n}=a^{m-n}$}\
&=0.66times 10^{5-(-3)}\
&=0.66times 10^8\
&=0.66times 10 times 10^7\
&boxed{=6.6times 10^7}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
& left ( dfrac{-3x^2}{y^{-2}} right)^3tag{use $(dfrac{a}{b})^m=dfrac{a^m}{b^m}$}\
&= dfrac{(-3x^2)^3}{(y^{-2})^3} tag{use $(ab)^m=a^mb^m$}\
&=dfrac{(-3)^3(x^2)^3}{(y^{-2})^3} tag{use $(a^m)^n=a^{mcdot n}$}\
&=dfrac{-27x^{2cdot 3}}{y^{-2cdot 3}}\
&=dfrac{-27x^6}{y^{-6}}tag{use $dfrac{1}{a^{-m}}=a^m$}\
&=-27x^{6}(y^6)\
&boxed{=-27x^{6}y^6}
end{align*}
$$
$$
begin{align*}
&(3x+4)(4y-1)tag{use distributive property}\
&=3x(4y-1)+4(4y-1)\
&=3xcdot 4y+3xcdot -1+4cdot 4y+4cdot -1\
&boxed{=12xy-3x+16y-4}
end{align*}
$$
$textbf{(d)}$
$$
begin{align*}
&(x-2)^2+2tag{use $(a-b)^2=(a-b)cdot (a-b)$}\
&=(x-2)cdot (x-2)+2\
&=x(x-2)-2cdot (x-2)+2\
&=xcdot x+xcdot (-2)+(-2)cdot x+(-2)cdot (-2)+2\
&=x^2+-2x-2x+4+2\
&boxed{=x^2-4x+6}
end{align*}
$$
$textbf{(b)}$ $-27x^{6}y^6$
$textbf{(c)}$ $12xy-3x+16y-4$
$textbf{(d)}$ $x^2-4x+6$
$textbf{(b)}$ The $R$-squared value can be calculated by squaring the given correlation coefficient $(r)$.
$Rightarrow$
$$
R-text{squared value}=r^2=(-0.66)^2=0.4356
$$
The value of $R^2=0.4356$ signifies that 43 percent variation in the weight of the backpack can be predicted by the number of quarter passed in the high school and the rest 57 percent variation depends on the other factors.
$textbf{(c)}$ The residual with the greatest magnitude is $|-6.5|=6.5$ which corresponds to the point $(3,5.96)$
$textbf{(d)}$ For estimating the weight of a backpack for a student who has completed 10 quarters of high school we need to put $x=10$ into the LSRL equation.
$$
begin{align*}
y&=13.84-0.55x\
y&=13.84-0.55(10)\
y&=13.84-5.5\
y&=8.34 text{ lbs}
end{align*}
$$
$textbf{(e)}$ No, the magnitude of the residuals are big and the correlation coefficient is moderate so this linear model is not very good to predict the backpack weight. Also, from the $R$-squared value we can see that almost 57 percent variation in the weight of the backpack is dependent on the other factors.
$textbf{(b)}$ The value of $R^2=0.4356$ signifies that 43 percent variation in the weight of the backpack can be predicted by the number of quarter passed in the high school and the rest 57 percent variation depends on the other factors.
$textbf{(c)}$ The residual with the greatest magnitude is $|-6.5|=6.5$ which corresponds to the point $(3,5.96)$
$textbf{(d)}$ 8.34 lbs
$textbf{(e)}$ No, the magnitude of the residuals are big and the correlation coefficient is moderate so this linear model is not very good to predict the backpack weight.
Given that $mangle ACB = mangle DCE$
and $mangle ABC = mangle CDE$. This implies the remaining angle of the triangles is equal to the each other which is $mangle BAC = mangle DEC$.
This means that the $Delta ABC sim Delta EDC$. Therefore, the ratio of the respective similar sides will be equal for each side.
$Rightarrow$
$$
begin{align*}
dfrac{AC}{EC}&=dfrac{BC}{DC}\\
dfrac{20}{x}&=dfrac{24}{x+2}tag{multiply each side by $(x+2)(x)$}\
dfrac{20}{x}cdot (x+2)(x) &=dfrac{24}{x+2}cdot (x+2)(x)\
20 cdot (x+2)&=24cdot x\
20x+40&=24xtag{subtract $ 20x$ from the each side}\
20x-20x+40&=24x-20x\
40&=4xtag{ divide each side by $4$}\
dfrac{40}{4}&=dfrac{4x}{4}\
x&=10
end{align*}
$$
Therefore, One side is 10 units and other is $10+2=12$ units long.
The third flowchart best represents what happened on Saturday. It clearly states the two given statements which were the reasons for the conclusion.
Flowchart 1 states that the second statement is an outcome of the first statement and later that the third statement is the outcome of the second statement. But that is incorrect. In fact the first and second statements are independent.
Flowchart 2 on the other hand makes it appear like a cyclic process, which means all the three statements are dependent on one another and using any two statements, one can conclude the third statement, which is not the case.
$$
mangle ADB=mangle CDB=90text{textdegree}
$$
$$
mangle ABD=mangle CBD
$$
The side BD is common for both the triangles. hence, we can write
$$
BD=BD
$$
So, in the given triangles we have two angles congruent with each other and the side between these angles is common and hence, the common side is congruent. So we can use ASA $cong$ rule to prove the congruence.
we can say that $boxed{Delta ADB cong Delta CDB}$ by ASA rule.
$textbf{(c)}$ From the given figure we can see that
$$
GH=EF
$$
$$
begin{align*}
FH=FH tag{common side}
end{align*}
$$
$$
mangle GFH=mangle EHF
$$
We can see that the angle is not between the known sides. So, SAS $cong$ is not applicable here. SSA is not sufficient for congruency and it may make different triangles. hence, we $textbf{ don’t have enough information to determine congruence.}$
$$
DC=BC=6
$$
$$
mangle DCE= mangle BCA
$$
We don’t have any other information about equality of sides or the angles. So,we $textbf{ don’t have enough information to determine congruence.}$
$textbf{(e)}$ From the given figure, we have
$$
mangle ADB= mangle BCA
$$
$$
mangle DBA= mangle CAB
$$
$$
begin{align*}
AB=ABtag{common side}
end{align*}
$$
So, in the given triangles we have two angles congruent with each other and a side is common for both the traingles therefore, the common side is congruent. So we can use AAS $cong$ rule to prove the congruence as the side is not between the congruent angles.
we can say that $boxed{Delta ADB cong Delta BCA}$ by AAS rule.
$textbf{(b)}$ $Delta ADB cong Delta CDB$ by ASA rule
$textbf{(c)}$ Don’t have enough information to determine congruence.
$textbf{(d)}$ Don’t have enough information to determine congruence.
$textbf{(e)}$ $Delta ADB cong Delta BCA$ by AAS rule.
A single rigid transformation that we shall need to perform is reflection of $triangle DBA$ over a mirror at the perpendicular bisector of side $BA$ then we will be able to map it over $triangle CAB$.
$triangle MNR; triangle NPR; triangle PQR; triangle QMR; triangle MNP; triangle MQP; triangle QMN; triangle QPN$
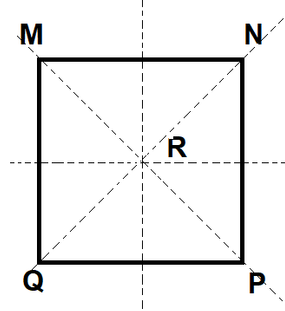
1.The diagonals are also angle bisectors.
2.Diagonals are perpendicular bisectors of each other at the intersection.
Hence we can conclude from statement 1:
$measuredangle RMN= measuredangle RNM = measuredangle RNP = measuredangle RPN= measuredangle RPQ= measuredangle RQP= measuredangle RQM = measuredangle RMQ = 45^{0}$
The following we can conclude from statement 2:
$MR = RP = NR = RQ$
Thus we can get the below congruence statements:
$triangle RMN cong triangle RNP cong triangle RQP cong triangle RQM$
$triangle PMN cong triangle PMQ cong triangle QNM cong triangle QNP$
$triangle ABC cong triangle ADC$ by AAS $cong$
Here we are given that $measuredangle BAC cong measuredangle DAC; measuredangle B cong measuredangle D$.
Also $AC cong AC$ by reflexive property.
We can’t say that if $triangle PLM cong triangle ONM$ as there is no statement comparing the side lengths of each triangle.
$$
triangle WXY cong triangle TZY
$$
We are given that $measuredangle X cong measuredangle Z; measuredangle WYX cong measuredangle TYZ$.
Also $WY cong TY; XY cong ZY$
Hence the triangles are congruent by SAS and ASA and AAS test of similarity.
It is given that $triangle XYZ$ was reflected across $XZ$.
To take the reflection of side $XY$, we shall take reflection of point $X$ and point $Y$ and then join those reflected points. Since $X$ lies on the line $XZ$, $X’$ shall be on X. To find $Y’$, we shall drop a perpendicular on $XZ$ from $Y$ and extend it such that $YZ = Y’Z$
Now since when we know that Y and Y’ are mirror images, they would lie on the same perpendicular line to XZ, hence they lie on the same straight line.
$triangle XYZ cong triangle XY’Z$
Since they are mirror images of each other,
$XY cong XY’$ (Mirror images of each other)
$YZ cong Y’Z$ (Mirror images of each other)
$XZ cong XZ$ (Reflexive property)
In earlier solution we concluded that $triangle XYZ cong triangle XY’Z$
Hence,
$measuredangle ZXY cong measuredangle ZXY’$
$measuredangle Y cong measuredangle Y’$
$measuredangle YZX cong measuredangle Y’ZX$
$XY cong XY’$
$YZ cong Y’Z$
$XZ cong XZ$
Let $a_n$ represent the $n^text{th}$ term corresponding to the term number $n$. we can find the difference in the consecutive terms as shown below.
$$
begin{align*}
a_2-a_1&=120-108=12\
a_3-a_2&=132-120=12\
a_{n+1}&-a_n=12tag{ on generalising}\
a_{n+1}&=a_n+12tag{on rearranging}
end{align*}
$$
The recursvive equation for this sequence is
$$
boxed{a_{n+1}=a_n+12}
$$
$textbf{(b)}$ The given sequence is $dfrac{2}{5},dfrac{4}{5},dfrac{8}{5},cdots$
Let $a_n$ represent the $n^text{th}$ term corresponding to the term number $n$. we can find the ratio between the consecutive terms as shown below.
$$
begin{align*}
dfrac{a_2}{a_1}&=dfrac{4/5}{2/5}=dfrac{4}{2}=2\
dfrac{a_3}{a_2}&=dfrac{8/5}{4/5}=dfrac{8}{4}=2\
&dfrac{a_{n+1}}{a_n}=2 tag{on generalising}\
&a_{n+1}=2cdot a_n tag{on rearranging}
end{align*}
$$
The recursvive equation for this sequence is
$$
boxed{a_{n+1}=2cdot a_n}
$$
Let $t(n)$ represent the $n^text{th}$ term corresponding to the term number $n$. So we can represent each term as shown below.
$$
begin{align*}
t(1)&=3741\
t(2)&=3702=3741-39=3741-1cdot 39=3741-(2-1)cdot 39\
t(3)&=3663=3741-39-39=3741-2cdot 39=3741-(3-1)cdot 39\
t(n)&=3741-(n-1)cdot 39
end{align*}
$$
The explicit equation for the given sequence is
$$
boxed{t(n)=3741-(n-1)cdot 39}
$$
$textbf{(d)}$ The given sequence is $117, 23.4, 4.68,cdots$
Let $t(n)$ represent the $n^text{th}$ term corresponding to the term number $n$. So we can represent each term as shown below.
$$
begin{align*}
t(1)&=117=117cdot 1=117cdot (0.2)^0\
t(2)&=23.4=170cdot (0.2)=170cdot (0.2)^{2-1}\
t(3)&=4.68=170cdot (0.2)cdot (0.2)=170cdot (0.2)^{3-1}\
t(n)&=117cdot (0.2)^{n-1}
end{align*}
$$
The explicit equation for the given sequence is
$$
boxed{t(n)=117cdot (0.2)^{n-1}}
$$
$textbf{(b)}$ $a_{n+1}=2cdot a_n$
$textbf{(c)}$ $t(n)=3741-(n-1)cdot 39$
$textbf{(d)}$ $t(n)=117cdot (0.2)^{n-1}$
$$
Rightarrow
$$
$$
begin{align*}
mangle D+mangle F+mangle E&=180text{textdegree}\
48text{textdegree}+117text{textdegree}+mangle E&=180text{textdegree}\
165text{textdegree}+mangle E&=180text{textdegree}tag{subtract $ 165text{textdegree}$ from the each side}\
mangle E&=180text{textdegree}-165text{textdegree}\
mangle E&=15text{textdegree}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
mangle D+mangle F+mangle E&=180text{textdegree}\
4x+2text{textdegree}+7x-8text{textdegree}+4x+6text{textdegree}&=180text{textdegree}\
(4x+7x+4x)+(2-8+6)text{textdegree}&=180text{textdegree}\
15x&=180text{textdegree}tag{ divide each side by $15$}\
dfrac{15x}{15}&=dfrac{180text{textdegree}}{15}\
x&=12text{textdegree}
end{align*}
$$
Therefore, $mangle D=4(12)+2text{textdegree}=50text{textdegree}$
$textbf{(c)}$ If all the angles of the triangle are equal then such triangle is called an equilateral triangle. Given that $mangle D=mangle F=mangle E$, therefore, the triangle $Delta FED$ is an equilateral triangle.
$textbf{(b)}$ $mangle D=50text{textdegree}$
$textbf{(c)}$ If all the angles of the triangle are equal then such triangle is called an equilateral triangle. Given that $mangle D=mangle F=mangle E$, therefore, the triangle $Delta FED$ is an equilateral triangle.
textbf{(a)}
$$
$$
begin{align}
y-3x&=-2\
4x+2y&=6
end{align}
$$
We can rearrange the equation (1) to write it as $y=3x-2$ then we can solve the system by using Substitution method. Substitute the $y=3x-2$ into the equation (2) and solve for $x$ into the resulting equation.
$$
begin{align*}
4x+2y&=6\
4x+2(3x-2)&=6\
4x+6x-4&=6\
10x-4&=6tag{ add $ 4$ to the each side}\
10x-4+4&=6+4\
10x&=10tag{ divide each side by $10 $}\
dfrac{10x}{10}&=dfrac{10}{10}\
x&=1
end{align*}
$$
put $x=1$ into the equation $y=3x-2$ and solve for $y$.
$$
begin{align*}
y&=3x-2\
y&=3(1)-2\
y&=3-2\
y&=1
end{align*}
$$
Therefore , the solution point is $(1,1)$.
For drawing the graph , we need to find at least two set of points on each line so that we can locate them on the graph and easily draw a straight line passing through them. The graph is attached below and we can verify from the graph that the solution point is $(1,1)$ which is the intersection of both the lines on the graph.
$$
begin{align}
x&=y-4\
2x&-y=-5
end{align}
$$
Substitute the value of $x$ from the equation (1) into the equation (2) and solve for the $y$ into the resulting equation.
$$
begin{align*}
2x-y&=-5\
2(y-4)-y&=-5\
2y-8-y&=-5\
y-8&=-5tag{ add $8 $ to the each side}\
y-8+8&=-5+8\
y&=3
end{align*}
$$
put $y=3$ into $x=y-4$ and solve for $x$.
$$
begin{align*}
x&=y-4\
x&=(3)-4\
x&=-1
end{align*}
$$
Therefore, the solution point is $(-1,3)$.
For drawing the graph , we need to find at least two set of points on each line so that we can locate them on the graph and easily draw a straight line passing through them. The graph is attached below and we can verify from the graph that the solution point is $(-1,3)$ which is the intersection of both the lines on the graph.
$textbf{(b)}$ The solution point is $(-1,3)$
$$
(x,y) rightarrow (-y,x)
$$
$Rightarrow$ $A(-2,5)rightarrow A'(-5,-2)$.
We can also verify the result by drawing the graph for 90$text{textdegree}$ rotation as shown below.
A(-2,5)rightarrow A'(-5,-2)
$$
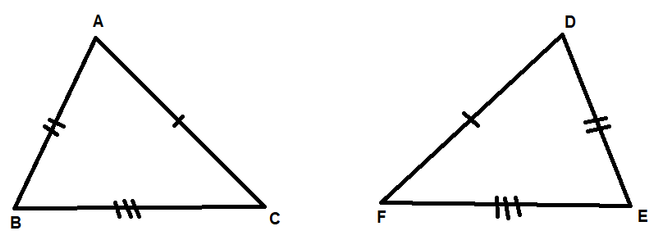
Yes if all three corresponding sides are congruent, then the triangles are congruent.
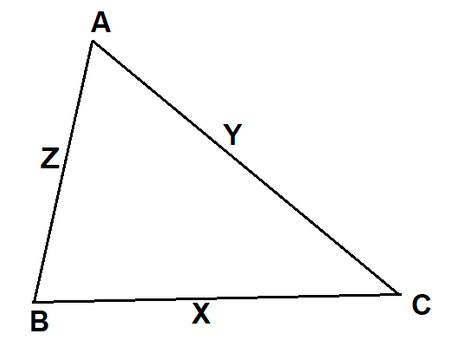
It isn’t possible to sketch a triangle which is having the same side lengths as compared to the earlier triangle and not be congruent.
In the right we can see that $triangle ABC cong triangle DEF$
Yes $SSS cong$ is a valid triangle congruence condition.
Thus by just having two corresponding sides congruent we can’t determine if the pair of triangles are congruent.
By the Pythagoras theorem,
$$
begin{align*}
DE^{2}+DF^{2} &= EF^{2} \
DF^{2} &=EF^{2}-DE^{2} \
AB^{2}+AC^{2} &=BC^{2} \
AC^{2} &=BC^{2}-AB^{2} \
end{align*}
$$
Now since it was given that $AB=DE, EF=BC$ we can conclude that $DF=AC$. The $triangle ABC cong triangle DEF$ by $SSS$ congruence test.
This test is also know as $RHS cong$ that is Right-angled Hypotenuse Side test

We can see the $triangle ABC$ is having two sides 4cm, 5cm and the included angle $20^{o}$.
It is not possible to create another triangle with same measurements which isn’t congruent. Both the triangles shall become congruent by SAS $cong$.
As we can see from the triangle drawn in the above diagram, we have 2 triangles $triangle ABC text{ and } triangle DEF$ which are congruent by SAS $cong$.
Hence it is not possible to draw 2 triangles which are not congruent but with the same measurements.
SAS $cong$ is a deterministic test for triangle congruency. When we observe the triangles in part (a), we can perform rigid transformations like rotation and map the two triangles onto each other. For part (b) we can performa couple of reflections and we can map the two triangles. This proves that SAS$cong$ is a test to determine of two triangles are congruent.
We can see that SSA is not a valid triangle test.
List of valid triangle congruence conditions are (without extra information): SSS, SAS, ASA, AAS, RHS (Right angle, Hypotenuse, Side). All the others are carrying extra information or are the repetition of these tests.

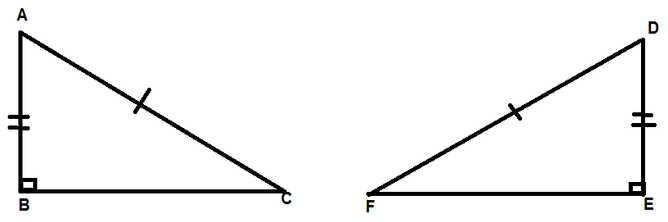
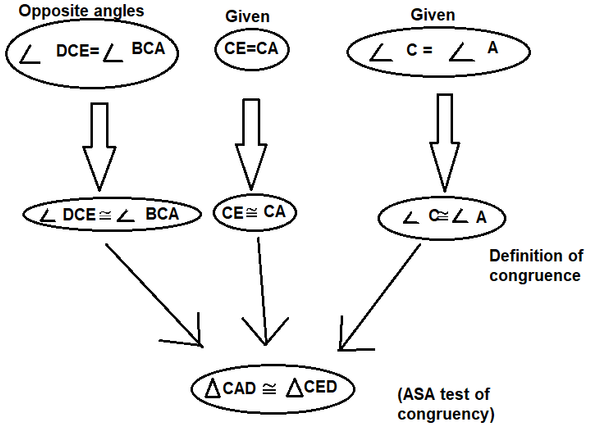
$triangle CAB cong triangle CED$ by ASA $cong$
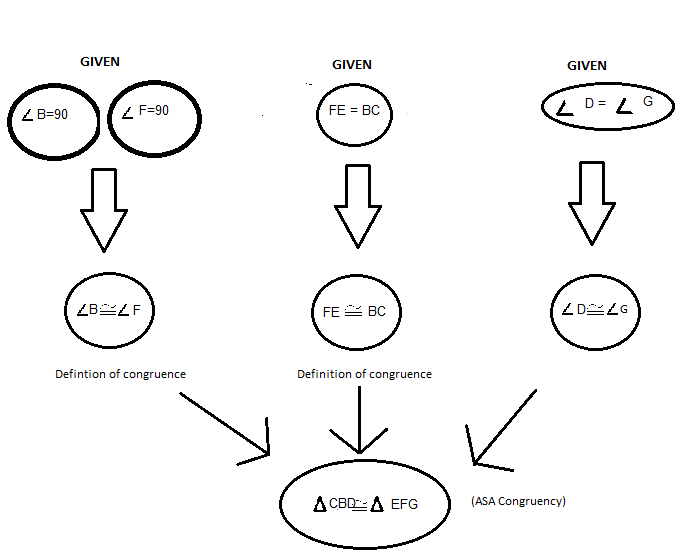
$triangle CBD cong triangle EFG$ by AAS $cong$
Here we can not say if the triangles are congruent because, $triangle ILJ$ the side which is between the two congruent angles is congruent to another side in $triangle KHM$. Hence two corresponding sides are not congruent.Thus we can’t comment if the triangles are congruent.
Here we know that the triangles are similar as all three angles are congruent. But since we do not know anything about any of the sides, we can’t comment if they are congruent.
$$
begin{align}
y+3x&=-10\
5x-y&=2
end{align}
$$
The given system can be solved using elimination method. We can combine both the equation to eliminate the $y$ and solve for $x$ from the resulting equation.
$$
begin{align*}
y+3x&=-10\
+(5x-y)&+(2)\
y-y+3x+5x&=-10+2\
8x&=-8tag{ divide each side by $8$}\
dfrac{8x}{8}&=dfrac{-8}{8}\
x&=-1
end{align*}
$$
Put $x=-1$ into the equation (1) and solve for $x$.
$$
begin{align*}
y+3(-1)&=-10\
y-3&=-10tag{ add $3 $ to the each side}\
y&=-10+3\
y&=-7
end{align*}
$$
The solution point is $(-1,-7)$
textbf{(b)}
$$
$$
begin{align}
6x&=7-2y\
4x&+y=4
end{align}
$$
We can rearrange equation (2) to write it as $y=-4x+4$, the we can substitute the value of $y$ from this reformed equation into the equation (1) and solve for $x$.
$$
begin{align*}
6x&=7-2y\
6x&=7-2(-4x+4)\
6x&=7+8x-8\
6x&=8x-1tag{subtract $6x$ from the each side}\
6x-6x&=8x-6x-1\
0&=2x-1\
2x&=1\
x&=dfrac{1}{2}
end{align*}
$$
put $x=dfrac{1}{2}$ into the equation $y=-4x+4$ and solve for $y$.
$$
begin{align*}
y&=-4x+4\
y&=-4(dfrac{1}{2})+4\
y&=-2+4\
y&=2
end{align*}
$$
The solution point is $(dfrac{1}{2},2)$
$textbf{(b)}$ The solution point is $(dfrac{1}{2},2)$
Hence, the multiplier is 0.87
In this manner the point $(t,s)=(45,77)$ will give the least sum hence, It will be the best total score for Diego. The point is marked on the graph with a red color.
The association between the time taken and the number of strokes played is positive and which means with the increase in time, the number of strokes played increases.
$textbf{(c)}$ The point is $(t,s)=(92,90)$. This point best represent the situation when he was suffering from seasonal allergies. He took more time to score 90 strokes whereas, in normal condition for scoring 91 strokes he took only 58 minutes.
From intuition, the line of best fit should pass through $(45,77)$ and $(56,86)$.
Slope of a line which passes through a pair or points $(t_1,s_1)$ and $(t_2,s_2)$ is given by
$$
text{slope}=dfrac{s_2-s_1}{t_2-t_1}
$$
Now, we have given points as $(45,77)$ and $(56,86)$. Let $(t_1,s_1)=(45,77)$ and $(t_2,s_2)=(56,86)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{86-77}{56-45}\
&=dfrac{9}{11}\
&=0.8182
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(t_1,s_1)$ is given by
$$
s-s_1=mcdot (t-t_1)
$$
Therefore, the equation of a line of slope $0.8182$ passing through a point $(45,77)$ is given by
$$
begin{align*}
s-(77)&=0.8182cdot (t-45)\
s-77&=0.8182cdot t +0.8182cdot (-45)\
s&=0.8182cdot t -36.8182 +77\
&boxed{s=0.8182t+40.1818}
end{align*}
$$
$textbf{(e)}$ Yes, Diego should train to reduce his time so that he sees a decrease in his golf score. In real life, it is unlikely that the number of strokes played to complete a course will decrease with the decrease in the time but from the given data, we can advise that.
$textbf{(b)}$ The association between the time taken and the number of strokes played is positive and which means with the increase in time, the number of strokes played increases.
$textbf{(c)}$ $s=0.8182t+40.1818$
$textbf{(d)}$ The slope of the trend line is $0.8182$ which represents the number of strokes played per minute.
$textbf{(e)}$ Yes, Diego should train to reduce his time so that he sees a decrease in his golf score. In real life, it is unlikely that the number of strokes played to complete a course will decrease with the decrease in the time but from the given data, we can advise that.
$$
begin{align*}
V&=LWHtag{ divide each side by $LH $}\
dfrac{V}{LH}&=left ( dfrac{LH}{LH} right)(W)\
dfrac{V}{LH}&=W
end{align*}
$$
The equation the the form of $W=cdots$ is $boxed{W=dfrac{V}{LH}}$
$textbf{(b)}$ Solving for $x$
$$
begin{align*}
y&=dfrac{x}{2}+3tag{subtract $3 $ from the each side}\
y-3&=dfrac{x}{2}+3-3\
y-3&=dfrac{x}{2}tag{multiply each side by 2}\
(y-3)cdot 2&=dfrac{x}{2}cdot 2\
2y-6&=x\
&boxed{x=2y-6}
end{align*}
$$
$$
begin{align*}
dfrac{E}{R}&=I tag{multiply each side by $R$}\
dfrac{E}{R}cdot R&=I cdot R\
E&=IRtag{ divide each side by $ I$}\
dfrac{E}{I}&=dfrac{IR}{I}\
dfrac{E}{I}&=R\
&boxed{R=dfrac{E}{I}}
end{align*}
$$
$$
textbf{(d)}
$$
$$
begin{align*}
2x+dfrac{1}{y}&=3tag{subtract $2x$ from the each side}\
2x-2x+dfrac{1}{y}&=3-2x\
dfrac{1}{y}&=3-2xtag{multiply each side by $y$}\
dfrac{1}{y}cdot y&=(3-2x)cdot y\
1&=(3-2x)ytag{ divide each side by $3-2x$}\
dfrac{1}{3-2x}&=dfrac{(3-2x)y}{3-2x}\
&boxed{y=dfrac{1}{3-2x}}
end{align*}
$$
$textbf{(b)}$ $x=2y-6$
$textbf{(c)}$ $R=dfrac{E}{I}$
$textbf{(d)}$ $y=dfrac{1}{3-2x}$
$$
begin{align*}
text {Speed of boat in still water} &= 8 text{miles/hour}\
text {Current of river} &= 2 text{miles/hour}
end{align*}
$$
$$
begin{align*}
text{Time taken to come upstream} &= dfrac{text{Distance to the crocodiles}}{text{Speed of the boat relative to ground}} \
&= y\
& =dfrac{x}{8-2}
end{align*}
$$
$$
begin{align*}
text{Time taken to go downstream} &= dfrac{text{Distance to the crocodiles} }{text{Speed of the boat relative to the ground}}\
&= y-1\
&= dfrac{x}{8+2}
end{align*}
$$
After solving the 1st equation we get, $6y=x$
After solving the 2nd equation we get $10y-10=x$
By solving the above equations, we get $y=dfrac{5}{2} text{ hours and } x = 15 text{ miles }$
Distance to the Crocodiles is 15 miles.
Hence total distance travelled by Maya is 30 miles.
{color{#4257b2}text{a)}}
$$
$$
begin{align*}
3x-7left(4+2xright)=-x+2& {;}quad : -11x-28=-x+2tag{Expand}\
&-11x-28+28=-x+2+28tag{Add 28 to both sides} \\
&-11x=-x+30tag{Simplify} \
&-11x+x=-x+30+xtag{Add x to both sides } \
&-10x=30tag{Simplify} \
&frac{-10x}{-10}=frac{30}{-10}tag{Divide both sides by -10} \
&{color{#c34632}x=-3}
end{align*}
$$
{color{#4257b2}text{b)}}
$$
$$
begin{align*}
-5x+2-x+1=0& {;}quad : -5x-x+1+2=0tag{Group like terms}\
&-6x+3=0tag{Simplify} \
&-6x+3-3=0-3tag{Subtract 3 from both sides} \
&-6x=-3tag{Simplify} \
&frac{-6x}{-6}=frac{-3}{-6}tag{Divide both sides by -6 } \
&{color{#c34632}x=frac{1}{2}}
end{align*}
$$
color{#4257b2} text{ a) }x=-3
$$
$$
color{#4257b2} text{ b) }x=frac{1}{2}
$$
$$
begin{align}
y&=-x-2\
5x&-3y=22
end{align}
$$
This pair of equation can be solved by substitution method. On putting $y=-x-2$ into the equation (2), it will result in an equation of single variable in terms of $x$ only.
$$
begin{align*}
5x-3y&=22\
5x-3(-x-2)&=22\
5x+3x+6&=22tag{subtract $6$ from the each side}\
8x+6-6&=22-6\
8x&=16tag{ divide each side by $8 $}\
dfrac{8x}{8}&=dfrac{16}{8}\
x&=2
end{align*}
$$
We can solve for $y$ by putting $x=2$ into $y=-x-2$, which gives
$$
y=-(2)-2=-4
$$
Therefore , the solution point is $(2,-4)$.
$$
x_{mid}=dfrac{x_1+x_2}{2}
$$
$textbf{(a)}$ We have $x_1=3$ and $x_2=9$
$Rightarrow$
$$
text{midpoint }=dfrac{9+3}{2}=6
$$
$textbf{(b)}$ We have $x_1=-1$ and $x_2=7$
$Rightarrow$
$$
text{midpoint }=dfrac{-1+7}{2}=3
$$
$textbf{(c)}$ We have $x_1=-15$ and $x_2=2$
$Rightarrow$
$$
text{midpoint }=dfrac{-15+2}{2}=-6.5
$$
$textbf{(b)}$ 3
$textbf{(c)}$ $-6.5$
We have
$mangle A=mangle G$
$mangle T=mangle I$
$mangle C=mangle P$
From AAA rule we can say that $Delta ATC sim Delta GIP$ but AAA is not sufficient condition for congruence, therefore, we need to prove at least one side of the triangle are congruent.
Let’s assume that $Delta ATC cong Delta GIP$. which means that sides $AT=GI$.
But it is given that $AT=4$
and $GI=6$. Therefore, our assumption is not correct and the triangles are not congruent with each other.
$$
16,000M+14,500J=120,000
$$
We can simplify the equation by diving each term by 100. which will give the equation
$$
boxed{160M+145J=1200}
$$
$textbf{(b)}$ We have 1 metric ton equivalent to 2200 pounds.
From the previous part, we have a yield from the Macintosh trees, equal to $16,000M$ pounds and yield of from the Jonathan trees equal to $14,500J$ pounds. So we can convert it into metric tons by dividing each of them by 2200.
$Rightarrow$
Yield from Macintosh trees $=dfrac{16000M}{2200}=7.272M$ metric tons.
Yield from Jonathan trees $=dfrac{14500J}{2200}=6.591J$ metric tons.
Now, we are given that Macintosh apples sell for $650 per metric ton and Jonathan apples sell for$700 per metric ton and the total production was worth $1,070,000. So, we can represent the situation by equation by multiplying the yield per metric ton by selling cost per metric ton. Therefore, the equation is given by
$$
begin{align*}
7.272Mtimes650+6.591Jtimes 700&=1,070,000\
4726.8M+4613.7J&=1,070,000
end{align*}
$$
$$
boxed{4726.8M+4613.7J=1,070,000}
$$
$textbf{(b)}$ $4726.8M+4613.7J=1,070,000$
$$
Rightarrow
$$
$$
begin{align*}
3x+13&=5x+2tag{subtract $3x $ from the each side}\
3x-3x+13&=5x-3x+2\
13&=2x+2tag{subtract $2$ from the each side}\
13-2&=2x+2-2\
11&=2xtag{ divide each side by $2$}\
dfrac{11}{2}&=dfrac{2x}{2}\
&boxed{x=dfrac{11}{2}}
end{align*}
$$
$textbf{(b)}$ In the figure, we marked the corresponding angles between the parallel lines ($7x-3text{textdegree}$ drawn in red colour). These should be equal. Also, Now $mangle {7x-3text{textdegree}}$ and $mangle {4x+12text{textdegree}}$ are the supplementary angles and their sum should be equal to 180$text{textdegree}$.
$Rightarrow$
$$
begin{align*}
7x-3text{textdegree}+4x+12text{textdegree}&=180text{textdegree}\
11x+9text{textdegree}&=180text{textdegree}tag{subtract $9text{textdegree}$ from the each side}\
11x&=180text{textdegree}-9text{textdegree}\
11x&=171text{textdegree}tag{ divide each side by $11$}\
dfrac{11x}{11}&=dfrac{171}{11}\
x&=dfrac{171}{11}\
&boxed{x= 15.54text{textdegree}}
end{align*}
$$
Now, we know that the sum of all the angles of a triangle is equal to 180$text{textdegree}$.
$$
Rightarrow
$$
$$
begin{align*}
110text{textdegree}+40text{textdegree}+x&=180text{textdegree}\
150text{textdegree}+x&=180text{textdegree}tag{subtract $150text{textdegree}$ from the each side}\
x&=180text{textdegree}-150text{textdegree}\
&boxed{x=30text{textdegree}}
end{align*}
$$
$textbf{(b)}$ $x=15.54 text{textdegree}$
$textbf{(c)}$ $x=30 text{textdegree}$
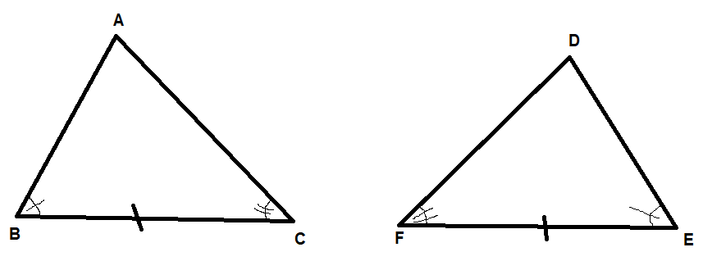
$bullet$ Reflection of $Delta AEB$ through a vertical line passing through point E.
$bullet$ Rotation through the centroid of the resultant triangle after reflection.
$textbf{(b)}$ The series of rigid transformations that would map $Delta AEB$ and $Delta CED$
Reflection of $Delta AEB$ through a vertical line passing through point E followed by Rotation through the centroid of the resultant triangle after reflection.
“cannot be determined”
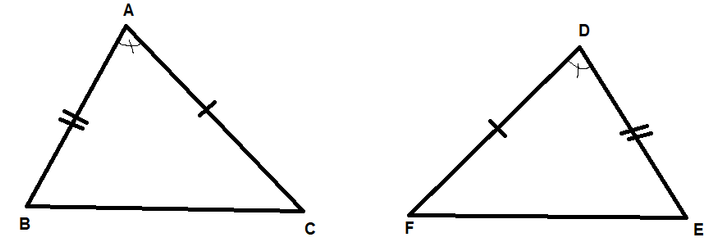
$textbf{(c)}$ We have all the three angles congruent. But AAA is not sufficient to prove congruence. We need at least one congruent side to prove congruence along with AAA condition.
“cannot be determined”
$textbf{(b)}$ cannot be determined
$textbf{(c)}$ cannot be determined
$textbf{(d)}$ Congruent by SSS rule
$textbf{(e)}$ Congruent by AAS rule
$bullet$ Equilateral triangle – It has all of its sides of equal length, as well as all three angles, are also equal.
$bullet$ Rectangle – A rectangle has four sides, which has all its four angles equal to 90$text{textdegree}$ and has an equal pair of opposite sides. The opposite sides of the rectangle are parallel to each other.
$bullet$ Parallelogram- It is a quadrilateral which has parallel opposite sides.
$bullet$ Kite- It has two equal pairs of disjoint adjacent sides. The two diagonals cut each other at an angle of 90$text{textdegree}$.
$bullet$ Trapezoid- A quadrilateral which has one pair of the parallel sides.
$bullet$ Square- A quadrilateral has all its four sides equal to each other and all of its angles are equal to 90$text{textdegree}$. The diagonals of the square bisect each other.
$bullet$ Rhombus- It has four equal sides. The diagonals bisect the vertex angles and cut each other perpendicularly.
We also have $mangle R =mangle C$, which means $mangle URN cong mangle ACT$.
Therefore, by using SAS congruence rule, we can say that
$$
Delta URN cong Delta ACT
$$
Hence, the given triangles are congruent. We can use translation as a rigid transformation to map one triangles onto the other.
$textbf{(a)}$ The length between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{Length}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$Rightarrow$
$$
begin{align*}
text{Length}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(3-(-5))^2+(1-7)^2}\
&=sqrt{8^2+(-6)^2}\
&=sqrt{64+36}\
&=sqrt{100}\
&=10
end{align*}
$$
Therefore, the length of the segment AB is 10 units.
$$
x_text{ midpoint}=dfrac{(x_2+x_1}{2}
$$
$$
y_text{ midpoint}=dfrac{(y_2+y_1}{2}
$$
$$
Rightarrow
$$
$$
x_text{ midpoint}=dfrac{(3+-5}{2}=-1
$$
$$
y_text{ midpoint}=dfrac{1+7}{2}=4
$$
Therefore, the coordinates of the midpoint are $(-1,4)$.
$textbf{(c)}$ Yes, we can find the length of the segment AC without using the pythagoras therorem. As we are given that the C is the middle point of the segment AB. Therefore it will didvide the segment AB into half. Hence, the length of the AC is the half of the length of AB
$Rightarrow$
$$
text{Length}_{AC}=dfrac{10}{2}=5 text{ units}
$$
$textbf{(b)}$ $(-1,4)$
$textbf{(c)}$ 5 units
$textbf{(a)}$ Two lines can have an infinite number of intersection points when they coincide with each other. Their equation should be identical when simplified.
Let’s assume the equation for our first line is $y=2x+3$. We can find the equation for the second line of the system by multiplying or dividing each term by any constant number and rearranging to look different than the first equation. In this way, these will represent the identical equation on simplification and will be coinciding when plotted on the graph.
$Rightarrow$ The equation of the second line is
$$
begin{align*}
2(y)&=2(2x+3)\
2y&=4x+6tag{subtract $4x$ from the each side}\
2y-4x&=4x-4x+6\
2y-4x&=6
end{align*}
$$
Therefore, we have our system of the equation as
$$
begin{align*}
y&=2x+3\
2&y-4x=6
end{align*}
$$
The graph of the system of lines is attached below. The lines are represented separately by displacing it a little bit, so that these are visible as different lines. Otherwise, Theoretically, these should coincide exactly.
we have our system of the equation as
$$
begin{align*}
y&=2x+3\
2&y-4x=6
end{align*}
$$
We can solve this system, using the Substitution method. Substitute the value of $y$ from the equation (1) into the equation $(2)$ and solve for $x$ from the resulting equation.
$$
begin{align*}
2y-4x&=6\
2(2x+3)-4x&=6\
4x+6-4x&=6\
6&=6tag{true always}
end{align*}
$$
We can see, that we obtained an equation which is free from any variable and true always. Therefore, our system has an infinite number of solutions.
Let’s assume the equation for our first line is $y=2x+3$. We can find the equation for the second line of the system by multiplying or dividing each term by any constant number and rearranging to look different than the first equation. In this way, these will represent the identical equation on simplification and will be coinciding when plotted on the graph.
$textbf{(b)}$ When solving for a system with the infinite solutions, we obtain an equation which is free of any variable and is true universally. So we can say that the equation has a solution which is independent of the value of $x$ and $y$ and therefore, they have an infinite number of solutions together.
Given that Apollo currently weighs 75 kg and is gaining 2 kg per month. So we can represent this situation by an equation shown below.
$$
y=2x+75
$$
It is also given that Zeus currently weighs 130 kg and is losing 3 kg per month. So we can represent this situation by an equation shown below.
$$
y=130-3x
$$
For finding the months when they both have the same weight, we need to equate the variable $y$ from both the equations, this will result into an equation only in terms of $x$ which on solving give the value for $x$.
$$
Rightarrow
$$
$$
begin{align*}
2x+75&=130-3xtag{ add $ 3x$ to the each side}\
2x+3x+75&=130-3x+3x\
5x+75&=130tag{subtract $75 $ from the each side}\
5x+75-75&=130-75\
5x&=55 tag{ divide each side by $5$}\
dfrac{5x}{5}&=dfrac{55}{5}\
x&=11text{ months}
end{align*}
$$
Therefore, after 11 months they will weigh the same. Yes, our solution does make sense in the context of this problem.
$bullet$ The slope of the LSRL equation is positive which means that per F$text{textdegree}$ change in the next day high temperature per F$text{textdegree}$ change in Random day’s high temperature, is positive and the graph is of increasing manner.
$bullet$ The given value of $r$ is equal to $0.928$. The value of $R^2$ can be calculated by squaring $r$.
$Rightarrow$
$$
R^2=(0.928)^2=0.8611
$$
The value of $R^2$ signifies that approximately 86 percent variation in the next day high temperature of any day can be predicted by the high temperature of its previous day and rest 14 percent variation is dependent upon the other factors.
$textbf{(b)}$ From the residual plot we can see that the highest magnitude of the residual is around $17$ F$text{textdegree}$.
The point which is most distant from the LSRL will correspond to this residual. By the graph of the points and the LSRL equation, we can see that the point $(70,90)$ is most distant from the LSRL. Hence the largest residual is 17F$text{textdegree}$ and it belongs to the point $(70,90)$.
$$
Rightarrow
$$
$$
begin{align*}
y&=13.17+0.85x\
y&=13.17+0.85(55)\
y&=13.17+46.75\
y&=59.92
end{align*}
$$
Therefore, tomorrow’s high temperature will be $59.92$ $text{textdegree}$, if today’s high temperature of Mitchell’s area is 55$text{textdegree}$.
$textbf{(d)}$ The maximum variation in the prediction we can say, varies by the highest value of the residual.
$Rightarrow$ Lower bound $=59.92-18=40.92text{textdegree}$
Upper bound $=59.92+17=76.92text{textdegree}$
No, Mitchell’s model is immature if we compare it with the models proposed by the professional meteorologists. We cannot rely on only 86 percent variation prediction of the previous day and exclude the 14 percent deciding factors. Moreover, the model itself has some large magnitudes of the residuals which can not be neglected.
The slope of the LSRL equation is positive which means that per F$text{textdegree}$ change in the next day high temperature per F$text{textdegree}$ change in Random day’s high temperature, is positive and the graph is of increasing manner.
The value of $R^2$ signifies that approximately 86 percent variation in the next day high temperature of any day can be predicted by the high temperature of its previous day and rest 14 percent variation is dependent upon the other factors.
$textbf{(b)}$ The largest residual is 17F$text{textdegree}$ and it belongs to the point $(70,90)$.
$textbf{(c)}$ Tomorrow’s high temperature will be $59.92$ $text{textdegree}$, if today’s high temperature of Mitchell’s area is 55$text{textdegree}$.
$textbf{(d)}$ Lower bound $=59.92-18=40.92text{textdegree}$
Upper bound $=59.92+17=76.92text{textdegree}$
No, Mitchell’s model is immature if we compare it with the models proposed by the professional meteorologists. We cannot rely on only 86 percent variation prediction of the previous day and exclude the 14 percent deciding factors. Moreover, the model itself has some large magnitudes of the residuals which cannot be neglected.
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$Rightarrow$
$$
begin{align*}
text{Length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(9-0)^2+(2-8)^2}\
&=sqrt{(9)^2+(-6)^2}\
&=sqrt{81+36}\
&=sqrt{117}\
&=10.82
end{align*}
$$
$$
begin{align*}
text{Length}_{CD}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(9-1)^2+(15-3)^2}\
&=sqrt{(8)^2+(12)^2}\
&=sqrt{64+144}\
&=sqrt{208}\
&=14.42
end{align*}
$$
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we are given points as $A(0,8)$ and $B(9,2)$. Let $(x_1,y_1)=(0,8)$ and $(x_2,y_2)=(9,2)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{2-8}{9-0}\
&=dfrac{-6}{9}\
&=-dfrac{2}{3}
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $-dfrac{2}{3}$ passing through a point $(0,8)$ is given by
$$
begin{align*}
y-(8)&=-dfrac{2}{3}cdot (x-0)\
y-8&=-dfrac{2}{3}cdot x\
&boxed{y=-dfrac{2}{3}x+8}
end{align*}
$$
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we are given points as $C(1,3)$ and $D(9,15)$. Let $(x_1,y_1)=(1,3)$ and $(x_2,y_2)=(9,15)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{15-3}{9-1}\
&=dfrac{12}{8}\
&=dfrac{3}{2}
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $dfrac{3}{2}$ passing through a point $(1,3)$ is given by
$$
begin{align*}
y-(3)&=dfrac{3}{2}cdot (x-1)\
y-3&=dfrac{3}{2}cdot x+dfrac{3}{2}cdot -1\
y&=dfrac{3}{2}cdot x-dfrac{3}{2}+3\
y&=dfrac{3}{2}cdot x+dfrac{-3+6}{2}\
&boxed{y=dfrac{3}{2}x+dfrac{3}{2}}
end{align*}
$$
The product of their slopes is
$$
-dfrac{2}{3}times dfrac{3}{2}=-1
$$
Therefore, the line segments $AB$ and $CD$ are perpendicular.
$textbf{(d)}$ The point of intersection of the $AB$ and $CD$ can be found out by solving for the solution of the system of equations of these lines.
$$
begin{align*}
y&=-dfrac{2}{3}x+8\
y&=dfrac{3}{2}x-dfrac{3}{2}
end{align*}
$$
We can solve this system by using Equal values method. Equate the $y$ variable of both the equations and solve for $x$ in the resulting equation.
$$
begin{align*}
-dfrac{2}{3}x+8&=dfrac{3}{2}x+dfrac{3}{2}tag{ add $ dfrac{2}{3}x$ to the each side}\
-dfrac{2}{3}x+dfrac{2}{3}x+8&=dfrac{3}{2}x+dfrac{2}{3}x+dfrac{3}{2}\
8=dfrac{9+4}{6}&x+dfrac{3}{2}tag{subtract $dfrac{3}{2} $ from the each side}\
8-dfrac{3}{2}=&dfrac{13}{6}x+dfrac{3}{2}-dfrac{3}{2}\
dfrac{16-3}{2}&=dfrac{13}{6}xtag{multiply each side by $dfrac{6}{13}$}\
dfrac{13}{2}cdot dfrac{6}{13}&=x\
x&=3
end{align*}
$$
Now put $x=3$ into the equation $y=-dfrac{2}{3}x+8$ and solve for $y$.
$$
begin{align*}
y&=-dfrac{2}{3}x+8\
y&=-dfrac{2}{3}(3)+8\
y&=-2+8\
y&=6
end{align*}
$$
Therefore, the point of intersection of $AB$ and $CD$ is $(3,6)$
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$textbf{(b)}$ $AB rightarrow y=-dfrac{2}{3}x+8$ and $CD rightarrow y=dfrac{3}{2}x+dfrac{3}{2}$
$textbf{(c)}$ The line segments $AB$ and $CD$ are perpendicular.
$textbf{(d)}$ The point of intersection of $AB$ and $CD$ is $(3,6)$
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$Rightarrow$
$$
begin{align*}
text{Length}_{SH}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(0-0)^2+(5-0)^2}\
&=sqrt{(25}\
&=5
end{align*}
$$
$$
begin{align*}
text{Length}_{HA}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(4-0)^2+(8-5)^2}\
&=sqrt{(16+9}\
&=sqrt{25}\
&=5
end{align*}
$$
$$
begin{align*}
text{Length}_{AY}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(7-4)^2+(4-8)^2}\
&=sqrt{(9+16}\
&=sqrt{25}\
&=5
end{align*}
$$
begin{align*}
text{Length}_{SY}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(7-0)^2+(4-0)^2}\
&=sqrt{(49+16}\
&=sqrt{65}\
&=8.062
end{align*}
$$
Therefore, the perimeter of the Shayla’s quadrilateral is given by
$$
begin{align*}
text{perimeter}&=text{Length}_{SH}+text{Length}_{HA}+text{Length}_{AY}+text{Length}_{SY}\
&=5+5+5+8.062\
&=23.0662
end{align*}
$$
$textbf{(b)}$ Two lines are parallel to each other if they have the same slopes. We can find the slope by using the method mentioned below.
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Let’s find out the slope of the line HA, with given points as $(0,5)$ and $(4,8)$. Let $(x_1,y_1)=(0,5)$ and $(x_2,y_2)=(4,8)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{8-5}{4-0}\
&=dfrac{3}{4}
end{align*}
$$
Now, Let’s find out the slope of the line SY, with given points as $(0,0)$ and $(7,4)$. Let $(x_1,y_1)=(0,0)$ and $(x_2,y_2)=(7,4)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{7-0}{4-0}\
&=dfrac{7}{4}
end{align*}
$$
We can see that sides HA ans SY has different slopes and hence these are not parallel. Similarly, we can easily see that side HS and AY cannot be parallel to each other as HS is vertical with infinite slope and AY is not vertical.
So, the quadrilateral SHAY does’not have any pair of parallel lines. Hence the quadrilateral SHAY is not a trapezoid and Shayla is incorrect.
$textbf{(d)}$ It does not have any special property expect it has equal length of its three sides, which we proved in part (a).
$textbf{(b)}$ The quadrilateral SHAY does’not have any pair of parallel lines. Hence, the quadrilateral SHAY is not a trapezoid and Shayla is incorrect.
$textbf{(c)}$ No, Shayla’s quadrilateral does not have any properties of another quadrilateral that we studied.
$textbf{(d)}$ It does not have any special property expect it has equal length of its three sides, which we proved in part (a).
$textbf{(a)}$ Let’s find out the length of each side by using the below mentioned distance formula.
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$Rightarrow$
$$
begin{align*}
text{Length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(6-1)^2+(6-4)^2}\
&=sqrt{(5)^2+(2)^2}\
&=sqrt{25+4}\
&=sqrt{29}\
&=5.39
end{align*}
$$
$$
begin{align*}
text{Length}_{BC}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(4-6)^2+(1-6)^2}\
&=sqrt{(-2)^2+(-5)^2}\
&=sqrt{4+25}\
&=sqrt{29}\
&=5.39
end{align*}
$$
begin{align*}
text{Length}_{CD}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(4-(-1))^2+(1-(-1))^2}\
&=sqrt{(5)^2+(2)^2}\
&=sqrt{25+4}\
&=sqrt{29}\
&=5.39
end{align*}
$$
$$
begin{align*}
text{Length}_{DA}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(-1-1)^2+(-1-4)^2}\
&=sqrt{(-2)^2+(-5)^2}\
&=sqrt{4+25}\
&=sqrt{29}\
&=5.39
end{align*}
$$
We can see that the quadrilateral $ABCD$ is having all its four sides of equal side length of 5.39 units. Therefore, we can say that $ABCD$ is a rhombus.
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we are given points as $A(1,4)$ and $C(4,1)$. Let $(x_1,y_1)=(1,4)$ and $(x_2,y_2)=(4,1)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{1-4}{4-1}\
&=dfrac{-3}{3}\
&=-1
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $-1$ passing through a point $(1,4)$ is given by
$$
begin{align*}
y-4&=-1cdot (x-1)\
y-4&=-1cdot x-1cdot (-1)\
y&=-x+1+4\
&boxed{y=-x+5}
end{align*}
$$
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we are given points as $B(6,6)$ and $D(-1,-1)$. Let $(x_1,y_1)=(-1,-1)$ and $(x_2,y_2)=(6,6))$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{6-(-1)}{6-(-1)}\
&=dfrac{7}{7}\
&=1
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $1$ passing through a point $(6,6)$ is given by
$$
begin{align*}
y-6&=1cdot (x-6)\
y-6&=1cdot x+1cdot 6\
y&=x+6+6\
&boxed{y=x+12}
end{align*}
$$
Tomika correctly heard that the diagonals of a rhombus are perpendicular to each other.
$textbf{(b)}$ The equation for $AC$ is $y=-x+5$ and the equation for $BD$ is $y=x+12$
$textbf{(c)}$ On comparing the slopes, we can see that $AC$ and $BD$ are perpendicular to each other. Therefore, Tomika correctly heard that the diagonals of a rhombus are perpendicular to each other.
In this way, we can see that the coordinates of the endpoints of the segment $a$ are $(2,3)$ and $(7,3)$.
The coordinates of the endpoints of the segment $b$ are $(-3,-1)$ and $(-3,4)$.
The coordinates of the endpoints of the segment $c$ are $(-2,-2)$ and $(5,-2)$.
Now, the midpoint of any segment with the given endpoint coordinates $(x_1,y_1)$ and $x_2,y_2$ is given by
$$
text{midpoint}_{x}=dfrac{x_1+x_2}{2}
$$
$$
text{midpoint}_{y}=dfrac{y_1+y_2}{2}
$$
$bullet$ Midpoint of segment $a$ with endpoints $(2,3)$ and $(7,3)$.
$$
text{midpoint}_{x}=dfrac{2+7}{2}=dfrac{9}{2}=4.5
$$
$$
text{midpoint}_{y}=dfrac{3+3}{2}=3
$$
Therefore, the coordinates of the midpoint of the segment $a$ are $(4.5,3)$
$bullet$ Midpoint of segment $b$ with endpoints $(-3,-1)$ and $(-3,4)$.
$$
text{midpoint}_{x}=dfrac{-3+-3}{2}=-3
$$
$$
text{midpoint}_{y}=dfrac{-1+4}{2}=dfrac{3}{2}=1.5
$$
Therefore, the coordinates of the midpoint of the segment $b$ are $(-3,1.5)$
$bullet$ Midpoint of segment $c$ with endpoints $(-2,-2)$ and $(5,-2)$.
$$
text{midpoint}_{x}=dfrac{-2+5}{2}=dfrac{3}{2}=1.5
$$
$$
text{midpoint}_{y}=dfrac{-2+-2}{2}=-2
$$
Therefore, the coordinates of the midpoint of the segment $c$ are $(1.5,-2)$
The coordinates of the midpoint of the segment $b$ are $(-3,1.5)$
The coordinates of the midpoint of the segment $c$ are $(1.5,-2)$
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we are given the points $(-24,7)$ and $(30,25)$. Let $(x_1,y_1)=(-24,7)$ and $(x_2,y_2)=(30,25)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{25-7}{30-(-24)}\
&=dfrac{18}{54}\
&=dfrac{1}{3}
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $dfrac{1}{3}$ passing through a point $(30,25)$ is given by
$$
begin{align*}
y-25&=dfrac{1}{3}cdot (x-30)\
y-25&=dfrac{1}{3}cdot x+dfrac{1}{3}cdot (-30)\
y-25&=dfrac{1}{3}cdot x-10\
y&=dfrac{1}{3}cdot x-10+25\
&boxed{y=dfrac{1}{3} x+15}
end{align*}
$$
$$
begin{align*}
y&=dfrac{1}{3}x+15\
(33)&=dfrac{1}{3}(51)+15\
33&=17+15\
33&=32tag{not true}
end{align*}
$$
Therefore, the point $(51,33)$ does not lie on the given line.
$textbf{(b)}$ The point $(51,33)$ does not lie on the given line.
$$
begin{align*}
dfrac{x}{4}-dfrac{x}{6}&=dfrac{2}{3}tag{multiply each side by LCM of 6 and 4 (12)}\
dfrac{x}{4}cdot 12-dfrac{x}{6}cdot 12&=dfrac{2}{3}cdot 12\
3x-2x&=2cdot 4\
&boxed{x=8}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
5^{3x}&=25^{(x+2)}tag{write 25 as $5^2$}\
5^{3x}&=(5^2)^{(x+2)}tag{use $(a^m)^n=a^{mcdot n}$}\
5^{3x}&=5^{2cdot (x+2)}tag{equate powers, as base is same}\
3x&=2(x+2)\
3x&=2x+4tag{subtract $2x$ from the each side}\
3x-2x&=2x-2x+4\
&boxed{x=4}
end{align*}
$$
$textbf{(b)}$ $x=4$
$textbf{(b)}$
The labelled figure with the flowchart is attached below.
$textbf{(b)}$ Congruent by ASA rule.
$textbf{(c)}$ Congruent by RH or SSS rule.
$textbf{(d)}$ Not congruent
Let’s the slope of the lines is $3$, assuming the first line has $y$-intercept equal to $4$ and the second line has $y$-intercept equal to $6$.
$$
Rightarrow
$$
$$
begin{align}
y&=3x+4\
y&=3x+6
end{align}
$$
The given system has no solutions because from the graph attached below we can see that they never intersect each other at any point.
$$
begin{align}
y&=3x+4\
y&=3x+6
end{align}
$$
We can solve the system by using Equal value method. Equate the variable $y$ of both equations and try to solve for the value of $x$.
$$
Rightarrow
$$
$$
begin{align*}
3x+4&=3x+6tag{subtract $3x $ from the each side}\
3x-3x+4&=3x-3x+6\
4&=6tag{not true}
end{align*}
$$
In the case of the system with no solutions , we get a non true equality, which shows that your equation is incorrect which means the given system doesn’t have any possible solution.
$$
begin{align*}
y&=3x+4\
y&=3x+6
end{align*}
$$
$textbf{(b)}$ In the case of the system with no solutions, we get a non-true equality, which shows that your equation is incorrect which means the given system doesn’t have any possible solution.
Given that $D$ and $E$ are the midpoints of the respective sides. this implies
$$
DB=dfrac{1}{2}AB
$$
$$
BE=dfrac{1}{2}BC
$$
we can also see that $angle B$ is common to both the smaller and bigger triangle. Therefore using SAS rule we can say that $Delta DBE sim Delta ABC$.
Now, scaling factor for this case is $dfrac{1}{2}$ by assuming $Delta ABC$ as original triangle. Because each side is scaled in the same proportion.
$$
Rightarrow
$$
$$
dfrac{BD}{AB}=dfrac{BE}{BC}=dfrac{DE}{AC}=dfrac{1}{2}
$$
Therefore, we can say that the length of $DE$ is equal to the half the length of $AC$.
$$
text{midpoint}(x,y)=left ( dfrac{x_1+x_2}{2} right),left (dfrac{y_1+y_2}{2} right)
$$
$bullet$ Finding the midpoint of segment $AB$ with end point coordinates $A(0,0)$ and $B(2,6)$. Let $(x_1,y_1)=(0,0)$ and $(x_2,y_2)=(2,6)$
$Rightarrow$
$$
text{midpoint}_x=dfrac{0+2}{2}=1
$$
$$
text{midpoint}_y=dfrac{0+6}{2}=3
$$
Therefore, the coordinates of the point $D$ are $(1,3)$.
similarly, we can find the coordinates of the point $E$ which is midpoint of the segment $BC$ with the endpoints $B(2,6)$ and $C(7,0)$.
$$
Rightarrow
$$
$$
text{midpoint}_x=dfrac{2+7}{2}=4.5
$$
$$
text{midpoint}_y=dfrac{6+0}{2}=3
$$
Therefore, the coordinates of the point $E$ are $(4.5,3)$
Given that $D$ and $E$ are the midpoints of the respective sides. this implies
$$
DB=dfrac{1}{2}AB
$$
$$
BE=dfrac{1}{2}BC
$$
we can also see that $angle B$ is common to both the smaller and bigger triangle. Therefore using SAS rule we can say that $Delta DBE sim Delta ABC$.
Now, scaling factor for this case is $dfrac{1}{2}$ by assuming $Delta ABC$ as original triangle. Because each side is scaled in the same proportion.
$$
Rightarrow
$$
$$
dfrac{BD}{AB}=dfrac{BE}{BC}=dfrac{DE}{AC}=dfrac{1}{2}
$$
Therefore, we can say that the length of $DE$ is equal to the half the length of $AC$.
$bullet$ For showing that $DE$ is parallel to $AC$ we need to show that these segments have equal slopes.The slopes for these segments can be calculated by the method explained below.
Slope of a line which passes through a pair of points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we are given the endpoints $A(0,0)$ and $C(7,0)$. Let $(x_1,y_1)=(0,0)$ and $(x_2,y_2)=(7,0)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{0-0}{7-0}\
&=dfrac{0}{7}\
&=0
end{align*}
$$
$bullet$ Calculating the slope of $DE$
we are given the endpoints $D(1,3)$ and $E(4.5,3)$. Let $(x_1,y_1)=(1,3)$ and $(x_2,y_2)=(4.5,3)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{3-3}{4.5-1}\
&=dfrac{0}{3.5}\
&=0
end{align*}
$$
We can see that the slopes of both the segments $AC$ and $DE$ are the same. Therefore, we can say that $DE$ is parallel to $AC$.
For calculating the perimeter of the $Delta ABC$ we need to find the length of each side.
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$
is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$bullet$ The legth of the side $AB$ with given end points $A(0,0)$ and B$(2,6)$ will be
$$
begin{align*}
text{length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(2-0)^2+(6-0)^2}\
&=sqrt{(2)^2+(6)^2}\
&=sqrt{4+36}\
&=sqrt{40}\
&=6.324
end{align*}
$$
$bullet$ The legth of the side $BC$ with given end points $B(2,6)$ and $C(7,0)$ will be
$$
begin{align*}
text{length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(7-2)^2+(0-6)^2}\
&=sqrt{(5)^2+(-6)^2}\
&=sqrt{25+36}\
&=sqrt{61}\
&=7.81
end{align*}
$$
$bullet$ The legth of the side $AC$ with given end points $A(0,0)$ and $C(7,0)$ will be
$$
begin{align*}
text{length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(7-0)^2+(0-0)^2}\
&=sqrt{(7)^2+(0)^2}\
&=sqrt{49}\
&=7
end{align*}
$$
Therefore, the perimeter of the $Delta ABC$ will be
$$
begin{align*}
text{Perimeter}&=text{Length}_{AB}+text{Length}_{BC}+text{Length}_{AC}\
&=6.324+7.81+7\
&=21.134
end{align*}
$$
We proved in the previous parts that the length of each side of the $Delta DBE$ is half the length of the respective sides of $Delta ABC$.
$Rightarrow$
$$
begin{align*}
text{Perimeter}&=text{Length}_{DB}+text{Length}_{BE}+text{Length}_{DE}\
&=dfrac{text{Length}_{AB}}{2}+dfrac{text{Length}_{BC}}{2}+dfrac{text{Length}_{AC}}{2}\
&=dfrac{6.324}{2}+dfrac{7.81}{2}+dfrac{7}{2}\
&=3.162+3.905+3.5\
&=10.567
end{align*}
$$
The perimeter of the $Delta DBE$ is half the perimeter of the $Delta ABC$.
The Area of any triangle is given by
$$
text{Area}=dfrac{1}{2}times text{Base}times text{perpendicular height}
$$
$bullet$ Calculating the area of $Delta ABC$
We have length of the base $text{length}_AC$ equal to $7$ units and perpendicular height from the graph is $6$ units. Therefore, the area of the $Delta ABC$ will be.
$$
begin{align*}
text{Area}_{ABC}&=dfrac{1}{2}times7times 6\
&=dfrac{42}{2}\
&=21
end{align*}
$$
$bullet$ Calculating the area of $Delta DBE$
We have length of the base $text{length}_AC$ equal to $dfrac{7}{2}=4.5$ units and perpendicular height from the graph is $3$ units. Therefore, the area of the $Delta ABC$ will be.
$$
begin{align*}
text{Area}_{DBE}&=dfrac{1}{2}times4.5times 3\
&=dfrac{13.5}{2}\
&=6.75
end{align*}
$$
Now, we can take the ratio of the areas of $Delta ABC$ and $Delta DBE$ to compare.
$$
dfrac{text{Area}_{ABC}}{text{Area}_{DBE}}=dfrac{21}{6.75}=4
$$
$Rightarrow$
$$
text{Area}_{ABC}=4times text{Area}_{DBE}
$$
$textbf{(b)}$ The coordinates of the point $D$ are $(1,3)$.
The coordinates of the point $E$ are $(4.5,3)$.
$textbf{(c)}$ The length of $DE$ is equal to the half the length of $AC$. Yes, $DE$ is parallel to $AC$.
$textbf{(d)}$ The perimeter of the $Delta DBE$ is half the perimeter of the $Delta ABC$.
$textbf{(e)}$ $text{Area}_{ABC}=4times text{Area}_{DBE}$
The midpoint of two point with the given coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{midpoint}_x=dfrac{x_1+x_2}{2}
$$
$$
text{midpoint}_y=dfrac{y_1+y_2}{2}
$$
Therefore, we can find the $x$ and $y$ coordinates of the midpoint for the given points $(3,1)$ and $(15,7)$.
$$
text{midpoint}_x=dfrac{3+15}{2}=dfrac{18}{2}=9
$$
$$
text{midpoint}_y=dfrac{1+7}{2}=dfrac{8}{2}=4
$$
therefore, the coordinates of the midpoint between the towns is $(9,4)$.
The distance between the any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
Therefore, distance between the town of Coyner and the woottonville can be found out by putting the coordinates into the above equation. Let $(x_1,y_1)=(3,1)$ and $(x_2,y_2)=(15,7)$
$Rightarrow$
$$
begin{align*}
text{distance}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(15-3)^2+(7-1)^2}\
&=sqrt{(12)^2+(6)^2}\
&=sqrt{144+36}\
&=sqrt{180}\
&=13.416
end{align*}
$$
The school is located at the midpoint of the town therefore it’s distance from each of the towns will be the half of the distance between the cities. Therefore, the distance will be $dfrac{13.416}{2}=6.708$ units.
$Rightarrow$
$R(1,7)$, $D(3,1)$ and $N(9,3)$.
We can find the distance between the vertex point to find the length of each side and compare if they are equal or not.
The distance between the any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
Therefore, the length of the side $RD$ is
$$
text{Length}_{RD}=sqrt{(3-1)^2+(1-7)^2}=sqrt{40}
$$
The length of the side $DN$ is
$$
text{Length}_{DN}=sqrt{(9-3)^2+(3-1)^2}=sqrt{40}
$$
We can see that the length of the $RD$ and $DN$ is equal. Let’s check if they are perpendicular to each other by finding their slopes and then checking if the product of their slopes is equal to $-1$ or not. If the product of slopes is $-1$ then these sides are perpendicular, otherwise they are not.
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
First, let’s find out the slope of the side $RD$. We are given the points $(1,7)$ and $(3,1)$. Let $(x_1,y_1)=(1,7)$ and $(x_2,y_2)=(3,1)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{1-7}{3-1}\
&=dfrac{-6}{2}\
&=-3
end{align*}
$$
Now, the slope of the side $DN$ with the points $(3,1)$ and $(9,3)$ will be. Let $(x_1,y_1)=(3,1)$ and $(x_2,y_2)=(9,3)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{3-1}{9-3}\
&=dfrac{2}{6}\
&=dfrac{1}{3}
end{align*}
$$
$$
-3times dfrac{1}{3}=-1
$$
Therefore, the taken sides are perpendicular to each other. Hence, we can say that the given triangle is indeed an isosceles right triangle because it has two of its sides equal and a right angle triangle.
$textbf{(b)}$ The perimeter of any polygon is the sum of its all sides. We have already calculated the two of its perpendicular sides and we can find the third by applying the Pythagoras theorem as shown below.
$$
begin{align*}
text{hypotenuse}&=sqrt{text{base}^2+text{perpendicular height}^2}\
RN&=sqrt{(DN)^2+(RD)^2}\
RN&=sqrt{(sqrt{40})^2+(sqrt{40})^2}\
RN&=sqrt{40+40}\
RN&=sqrt{80}\
RN&=8.944
end{align*}
$$
Therefore, the perimeter of the $Delta RDN$ is
$$
RD+DN+RN=(6.324+6.324+8.944)=21.592text{ units}
$$
Now , The area of a right-angled triangle is given by
$$
text{Area}=dfrac{1}{2}times text{Base}times text{Perpendicular height}
$$
We have Base $=6.324$ and $text{Perpendicular height}=6.324$, so the area will be equal to
$$
text{Area}=dfrac{1}{2}times 6.324times 6.324=19.996 text{ units}^2
$$
$textbf{(b)}$ Perimeter $=21.592$ units
Area $=19.996 text{ units}^2$
The midpoint of any given segment is the point on that segment which is equidistant from both its endpoints. The diagram is attached below.
In the figure, we have line segment $AB$ which is of length 8 units with the endpoints $A(1,3)$ and $B(9,3)$. Here, $C(5,3)$ is the midpoint of the segment which is dividing it in an equal length of 4 units and hence it is equidistant from both the ends.
We can determine the midpoint of any segment with the given endpoints $(x_1,y_1)$ and $(x_2,y_2)$ by the formula
$$
text{midpoint}_x=dfrac{x_1+x_2}{2}
$$
$$
text{midpoint}_y=dfrac{y_1+y_2}{2}
$$
We can determine the midpoint of any segment with the given endpoints $(x_1,y_1)$ and $(x_2,y_2)$ by the formula
$$
text{midpoint}_x=dfrac{x_1+x_2}{2}
$$
$$
text{midpoint}_y=dfrac{y_1+y_2}{2}
$$
$$
text{midpoint}(x,y)=left ( dfrac{x_1+x_2}{2} right),left (dfrac{y_1+y_2}{2} right)
$$
$bullet$ Finding the midpoint of segment $AD$ with end point coordinates $A(0,0)$ and $D(2,6)$. Let $(x_1,y_1)=(0,0)$ and $(x_2,y_2)=(2,6)$
$Rightarrow$
$$
text{midpoint}_x=dfrac{0+2}{2}=1
$$
$$
text{midpoint}_y=dfrac{0+6}{2}=3
$$
Therefore, the coordinates of the point $E$ are $(1,3)$.
$bullet$ Similarly, we can find the coordinates of the point $F$ which is midpoint of the segment $BC$ with the endpoints $B(9,0)$ and $C(5,6)$.
$$
Rightarrow
$$
$$
text{midpoint}_x=dfrac{9+5}{2}=7
$$
$$
text{midpoint}_y=dfrac{0+6}{2}=3
$$
Therefore, the coordinates of the point $F$ are $(7,3)$
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$
is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$bullet$ The legth of the side $AB$ with given end points $A(0,0)$ and B$(9,0)$ will be
$$
begin{align*}
text{length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(9-0)^2+(0-0)^2}\
&=sqrt{(9)^2+(0)^2}\
&=sqrt{81}\
&=9
end{align*}
$$
$bullet$ The legth of the side $DC$ with given end points $D(2,6)$ and $C(5,6)$ will be
$$
begin{align*}
text{length}_{DC}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(5-2)^2+(6-6)^2}\
&=sqrt{(3)^2+(0)^2}\
&=sqrt{9}\
&=3
end{align*}
$$
$bullet$ The legth of the side $EF$ with given end points $E(1,3)$ and $F(7,3)$ will be
$$
begin{align*}
text{length}_{EF}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(7-1)^2+(3-3)^2}\
&=sqrt{(6)^2+(0)^2}\
&=sqrt{36}\
&=6
end{align*}
$$
We can see that the length of the midsegment $EF$ is equal to the half of the sum of the lengths of both the bases. That is
$$
text{Length}_{EF}=dfrac{text{Length}_{AB}+text{Length}_{DC}}{2}=dfrac{9+3}{2}=6
$$
Let’s check if the midsegment $EF$ is parallel to bases $AB$ and $DC$ or not.
We already know that both the bases are parallel to each other which is an inherent property of a trapezoid. So we need to check with any one of the bases. Let’s check for the equality of slopes of the midsegment $EF$ and the base $AB$. First, we need to find the slopes by using the method shown below.
Slope of a line which passes through a pair of points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
$bullet$ Finding the slope of base $AB$
Now, we are given the points $A(0,0)$ and $B(9,0)$. Let $(x_1,y_1)=(0,0)$ and $(x_2,y_2)=(9,0)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{0-0}{9-0}\
&=dfrac{0}{9}\
&=0
end{align*}
$$
$bullet$ Finding the slope of midsegment $EF$
Now, we are given the points $E(1,3)$ and $F(7,3)$. Let $(x_1,y_1)=(1,3)$ and $(x_2,y_2)=(7,3)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{3-3}{7-1}\
&=dfrac{0}{6}\
&=0
end{align*}
$$
We can see that the slopes of Base $AB$ and midsegment $EF$ are equal. Therefore, we can say that the midsegment of a trapezoid is parallel to both of its bases.
The midpoint of any segment with given endpoint coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{midpoint}(x,y)=left ( dfrac{x_1+x_2}{2} right),left (dfrac{y_1+y_2}{2} right)
$$
$bullet$ Finding the midpoint of segment $AD$ with end point coordinates $A(-4,0)$ and $D(-2,2)$. Let $(x_1,y_1)=(-4,0)$ and $(x_2,y_2)=(-2,2)$
$Rightarrow$
$$
text{midpoint}_x=dfrac{-4+-2}{2}=-3
$$
$$
text{midpoint}_y=dfrac{0+2}{2}=1
$$
Let $E$ is the midpoint of the segment $AD$. Therefore, the coordinates of the point $E$ are $(-3,1)$.
$bullet$ Similarly, we can find the coordinates of the point $F$ which is midpoint of the segment $BC$ with the endpoints $B(2,0)$ and $C(0,2)$.
$$
Rightarrow
$$
$$
text{midpoint}_x=dfrac{2+0}{2}=1
$$
$$
text{midpoint}_y=dfrac{0+2}{2}=1
$$
Therefore, the coordinates of the point $F$ are $(1,1)$
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$
is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$bullet$ The legth of the side $AB$ with given end points $A(-4,0)$ and B$(2,0)$ will be
$$
begin{align*}
text{length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(2-(-4))^2+(0-0)^2}\
&=sqrt{(6)^2+(0)^2}\
&=sqrt{36}\
&=6
end{align*}
$$
$bullet$ The legth of the side $DC$ with given end points $D(-2,2)$ and $C(0,2)$ will be
$$
begin{align*}
text{length}_{DC}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(0-(-2))^2+(2-2)^2}\
&=sqrt{(2)^2+(0)^2}\
&=sqrt{4}\
&=2
end{align*}
$$
$bullet$ The legth of the side $EF$ with given end points $E(-3,1)$ and $F(1,1)$ will be
$$
begin{align*}
text{length}_{EF}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(1-(-3))^2+(1-1)^2}\
&=sqrt{(4)^2+(0)^2}\
&=sqrt{16}\
&=4
end{align*}
$$
Here also, we can see that the length of the midsegment $EF$ is equal to the half of the sum of the lengths of both the bases. That is
$$
text{Length}_{EF}=dfrac{text{Length}_{AB}+text{Length}_{DC}}{2}=dfrac{6+2}{2}=4
$$
Let’s check if the midsegment $EF$ is parallel to bases $AB$ and $DC$ or not.
We already know that both the bases are parallel to each other which is an inherent property of a trapezoid. So we need to check with any one of the bases. Let’s check for the equality of slopes of the midsegment $EF$ and the base $AB$. First, we need to find the slopes by using the method shown below.
Slope of a line which passes through a pair of points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
$bullet$ Finding the slope of base $AB$
Now, we are given the points $A(-4,0)$ and $B(2,0)$. Let $(x_1,y_1)=(-4,0)$ and $(x_2,y_2)=(2,0)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{0-0}{2-(-4)}\
&=dfrac{0}{6}\
&=0
end{align*}
$$
$bullet$ Finding the slope of midsegment $EF$
Now, we are given the points $E(-3,1)$ and $F(1,1)$. Let $(x_1,y_1)=(-3,1)$ and $(x_2,y_2)=(1,1)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{1-1}{1-(-3)}\
&=dfrac{0}{4}\
&=0
end{align*}
$$
We can see that the slopes of Base $AB$ and midsegment $EF$ are equal. Therefore, we can say that the midsegment of a trapezoid is parallel to both of its bases.
$textbf{(b)}$ Yes, the new trapezoid formed by the given set of points follows the same relationship as in part (a).
$textbf{(c)}$The midsegment of a trapezoid is parallel to the bases and is equal in length to the average of the lengths of the two bases.
We know that parallel sides have equal slope.
Therefore, If the slope of the line $AB$ is equal to the slope of the line $DC$ and slope of line $BC$ is equal to the slope of the line $AD$ then we can say that quadrilateral $ABCD$ is a parallelogram.
Slope of a line which passes through a pair of points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Therefore, slope of line $AB$ with endpoints $A(1,1)$ and $B(2,3)$ is
$$
begin{align*}
text{slope}_{AB}&= dfrac{3-1}{2-1}\
&=dfrac{2}{1}\
&=2\
end{align*}
$$
Slope of line $DC$ with endpoints $D(4,1)$ and $C(5,3)$ is
$$
begin{align*}
text{slope}_{DC}&= dfrac{3-1}{5-4}\
&=dfrac{2}{1}\
&=2\
end{align*}
$$
Since, slope of the line $AB$ is equal to the slope of the line $DC$ therefore $AB$ is parallel to $DC$.
$$
begin{align*}
text{slope}_{BC}&= dfrac{3-3}{5-2}\
&=dfrac{0}{3}\
&=0\
end{align*}
$$
Slope of line $AD$ with endpoints $A(1,1)$ and $D(4,1)$ is
$$
begin{align*}
text{slope}_{AD}&= dfrac{1-1}{4-1}\
&=dfrac{0}{3}\
&=0\
end{align*}
$$
Since, slope of the line $BC$ is equal to the slope of the line $AD$ therefore $BC$ is parallel to $AD$.
Thus, we get equal slopes for both the pairs of opposite sides of quadrilateral $ABCD$, therefore quadrilateral $ABCD$ is a parallelogram.
To draw the graph of any line we need any two points on the line so that we can locate these points on the graph and then we can easily draw a straight line passing through these points.
Let $x$-intercept and $y$-intercept are those two points. We already have $y$-intercept (0,-3) so only need to find the $x$-intercept .
$bullet$ For finding the $x$-intercept
Let $y=0$
$$
begin{align*}
y&=4x-3\
(0)&=4x-3tag{ add $3$ to the each side}\
3&=4xtag{ divide each side by $4$}\
dfrac{3}{4}&=x\
x&=0.75
end{align*}
$$
Therefore, the x-intercept is $(0.75,0)$.
Now we could draw the graph of $f(x)=4x-3$ by plotting both intercepts of this function as shown below.
$bullet$ For finding the $x$-intercept
Let $y=0$
$$
begin{align*}
y&=9x-13\
(0)&=9x-13tag{ add $13$ to the each side}\
13&=9xtag{ divide each side by $9$}\
dfrac{13}{9}&=x\
x&=1.44
end{align*}
$$
Therefore, the x-intercept is $left ( 1.44,0 right)$.
Now we could draw the graph of $f(x)=4x-3$ by plotting both intercepts of this function as shown below.
$$
Rightarrow
$$
$$
begin{align*}
4x-3&=9x-13tag{subtract $4x$ from the each side}\
4x-4x-3&=9x-4x-13\
-3&=5x-13tag{ add $ 13$ to the each side}\
-3+13&=5x-13+13\
10&=5xtag{ divide each side by $5$}\
dfrac{10}{5}&=dfrac{5x}{5}\
x&=2
end{align*}
$$
Now, put $x=2$ in equation $y=4x-3$ and solve for $y$.
$$
begin{align*}
y&=4x-3\
y&=4(2)-3\
y&=8-3\
y&=5
end{align*}
$$
Therefore, the intersection point is $(2,5)$.
The graph of both the lines along with the indicated point of intersection is attached below.
It is given that the number of bouquets sold was 15 more than the number of hearts sold. So, we can represent this situation by the equation shown below.
$$
x=y+15
$$
Given that the roses sold for $5 and the hearts sold for $3 and the club collected a total of $339. So this can be represented by the equation shown below.
$$
5x+3y=339
$$
We can solve this system of equation by using the Substitution method. We can substitute the value of $x$ from the first equation into the second equation $(5x+3y=339)$ and can solve for $y$ in the resulting equation in terms of a single variable $y$.
$$
Rightarrow
$$
$$
begin{align*}
5x+3y&=339\
5(y+15)+3y&=339\
5y+75+3y&=339tag{subtract $75$ from the each side}\
8y+75-75&=339-75\
8y&=264tag{ divide each side by $8$}\
dfrac{8y}{8}&=dfrac{264}{8}\
y&=33
end{align*}
$$
Now, put $y=33$ into equation $x=y+15$ and solve for $x$ as shown below.
$$
begin{align*}
x&=y+15\
x&=(33)+15\
x&=48
end{align*}
$$
Therefore, the number of rose bouquets sold on Valentine’s Day was 48 and the number of chocolate hearts sold was 33.
$$
t(n)=t(1)+(n-1)cdot d
$$
where, $t(n)$ is the term corresponding to the $n^text{th}$ term number and $t(1)$ is $1^text{st}$ term and $d$ is the common difference.
The difference between two consecutive terms of an arithmetic sequence is always equal when the term with lower term number is subtracted from the higher term number. This difference is called the common difference of the arithmetic progression.
A geometric sequence is a sequence when the ratio of two consecutive terms is equal for whole the sequence.
This ratio is called the common ratio $(r)$ for the geometric sequence and is defined as
$$
text{r}=dfrac{t(n+1)}{t(n)}
$$
For the given sequences we will first try to look for arithmetic sequence and check if the difference between the two consecutive terms is same or not. If it’s same then this sequence will be arithmetic and it is not an arithmetic then we will look for the geometric sequence by looking at the common ratio for the whole sequence.
If any sequence does not satisfy these two cases then it will not represents either arithmetic or geometric sequence.
$textbf{(a)}$ The given sequence is $1,4,7,10,13,cdots$
We can see that the difference between any two consecutive terms is the same and is equal to 3.
Therefore, the above sequence is an arithmetic sequence with the common difference $d=3$ and the $t(1)=1$. So we can put these values in the general term of the arithmetic sequence which is shown above.
$$
Rightarrow
$$
$$
begin{align*}
t(n)&=t(1)+(n-1)cdot d\
t(n)&=(1)+(n-1)cdot (3)\
&boxed{t(n)=1+(n-1)cdot 3}
end{align*}
$$
We can see that the difference between any two consecutive terms is not the same.
Therefore, the above sequence can not be an arithmetic sequence.
We can also see that this sequence also can not be a geometric sequence because when we try to find out the common ratio we will get a fraction with 0 in the denominator which will make the common ratio infinite. Therefore, Common ratio is not defined for this sequence.
In fact, 0 cannot be a term of any geometric sequence ever. This will create the same problem while calculating the common ratio $(r)$.
Hence, the given sequence is neither arithmetic nor geometric.
$textbf{(c)}$ The given sequence is $2,4,8,16,32,cdots$
We can see that the common ratio $r=dfrac{t(n+1)}{t(n)}=dfrac{4}{2}=dfrac{8}{4}=dfrac{16}{8}=dfrac{32}{16}=2$ is true for every consecutive terms of the sequence. Therefore, the given sequence is a geometric sequence.
$textbf{(d)}$ The given sequence is $5,12,19,26,cdots$
We can see that the difference between any two consecutive terms is same and is equal to $12-5=7$.
Therefore, the above sequence is an arithmetic sequence with the common difference $d=7$ and the $t(1)=5$. So we can put these values in the general term of arithmetic sequence.
$$
Rightarrow
$$
$$
begin{align*}
t(n)&=t(1)+(n-1)cdot d\
t(n)&=(5)+(n-1)cdot (7)\
&boxed{t(n)=5+(n-1)cdot 7}
end{align*}
$$
We can see that the difference between any two consecutive terms is same and is equal to $(x+1)-x=1$.
Therefore, the above sequence is an arithmetic sequence with the common difference $d=1$ and the $t(1)=x$. So we can put these values in the general term of arithmetic sequence.
$$
Rightarrow
$$
$$
begin{align*}
t(n)&=t(1)+(n-1)cdot d\
t(n)&=(x)+(n-1)cdot (1)\
t(n)&=x+(n-1)\
&boxed{t(n)=x+n-1}
end{align*}
$$
$textbf{(f)}$ The given sequence is $3,12,48,192,cdots$
We can see that the common ratio $r=dfrac{t(n+1)}{t(n)}=dfrac{12}{3}=dfrac{48}{12}=dfrac{192}{48}=4$ is true for every consecutive terms of the sequence. Therefore, the given sequence is a geometric sequence.
$textbf{(b)}$Neither arithmetic nor geometric.
$textbf{(c)}$ Geometric sequence with common ratio $r=2$
$textbf{(d)}$ Arithmetic Sequence with $d=7$ and equation of general term as $t(n)=5+(n-1)cdot 7$
$textbf{(e)}$ Arithmetic Sequence with common difference $d=1$ and equation of general term as $t(n)=x+n-1$
$textbf{(f)}$ Geometric sequence with common ratio $r=4$
To find the slope of equations of given lines we need to convert the lines into the slope-intercept form which is given by
$$
y=mx+c
$$
Where, $m$ represents the slope of the line and $c$ represents the $y$-intercept.
$$
textbf{(a)}
$$
$$
begin{align*}
-3x+y&=5\
-3x+3x+y&=5+3xtag{ add $3x$ to the each side}\
y&=3x+5
end{align*}
$$
On comparing with the slope-intercept form equation $y=mx+c$ we can see that the slope is equal to 3.
$$
textbf{(b)}
$$
$$
begin{align*}
-5x+y&=3\
-5x+5x+y&=3+5xtag{ add $5x$ to the each side}\
y&=5x+3
end{align*}
$$
On comparing with the slope-intercept form equation $y=mx+c$ we can see that the slope is equal to 5.
textbf{(c)}
$$
$$
begin{align*}
x+5y&=-15\
x-x+5y&=-15-xtag{ Subtract $x$ from the each side}\
5y&=-x-15tag{ divide each side by $5$}\
y&=dfrac{-x}{5}-3
end{align*}
$$
On comparing with the slope-intercept form equation $y=mx+c$ we can see that the slope is equal to $-dfrac{1}{5}$.
$$
textbf{(d)}
$$
$$
begin{align*}
-15x+5y&=-25\
-15x+15x+5y&=-25+15xtag{ add $15x$ to the each side}\
5y&=15x-25tag{ divide each side by $5$}\
y&=3x-5
end{align*}
$$
On comparing with the slope-intercept form equation $y=mx+c$ we can see that the slope is equal to $3$
Therefore, we can say that the equations given in the part $textbf{(a)}$ and $textbf{(d)}$ i.e. $-3x+y=5$ and $-15x+5y=-25$ are parallel to the each other.
Here, the slope of lines given in the part $textbf{(b)}$ and $textbf{(c)}$ is equal to $5$ and $dfrac{-1}{5}$ respectively. So the product of slopes is $5times -dfrac{1}{5}=-1$.
Hence lines $-5x+y=3$ and $x+5y=-15$ are perpendicular to each other.
The equations given in the part $textbf{(b)}$ and $textbf{(c)}$ i.e. $-5x+y=3$ and $x+5y=-15$ are perpendicular to each other.
$bullet$ Finding intersection point of $y=-dfrac{3}{2}x+3$ and $y=dfrac{3}{2}x-3$
We can solve this system by using Equal value method. We need to equate the value of the variable $y$ and solve for $x$ in the resulting equation in single variable in terms of $x$.
$$
Rightarrow
$$
$$
begin{align*}
-dfrac{3}{2}x+3 &=dfrac{3}{2}x-3 tag{ add $ dfrac{3}{2}x$ to the each side}\
-dfrac{3}{2}x+dfrac{3}{2}x+3 &=dfrac{3}{2}x+dfrac{3}{2}x-3\
3&=3x-3tag{ add $3$ to the each side}\
3+3&=3x-3+3\
6&=3xtag{ divide each side by $3$}\
dfrac{6}{3}&=dfrac{3x}{3}\
x&=2
end{align*}
$$
Now, put $x=2$ into $y=-dfrac{3}{2}x+3$ and solve for $y$.
$$
begin{align*}
y&=-dfrac{3}{2}x+3\
y&=-dfrac{3}{2}(2)+3\
y&=-3+3\
y&=0
end{align*}
$$
Therefore, the intersection point is $(2,0)$.
We can solve this system by using Equal value method. We need to equate the value of the variable $y$ and solve for $x$ in the resulting equation in single variable in terms of $x$.
$$
Rightarrow
$$
$$
begin{align*}
-dfrac{3}{2}x+3 &=dfrac{3}{2}x+3 tag{ add $ dfrac{3}{2}x$ to the each side}\
-dfrac{3}{2}x+dfrac{3}{2}x+3 &=dfrac{3}{2}x+dfrac{3}{2}x+3\
3&=3x+3tag{ subtract $3$ from the each side}\
3-3&=3x+3-3\
0&=3xtag{ divide each side by $3$}\
dfrac{0}{3}&=dfrac{3x}{3}\
x&=0
end{align*}
$$
Now, put $x=0$ into $y=-dfrac{3}{2}x+3$ and solve for $y$.
$$
begin{align*}
y&=-dfrac{3}{2}x+3\
y&=-dfrac{3}{2}(0)+3\
y&=0+3\
y&=3
end{align*}
$$
Therefore, the intersection point is $(0,3)$.
$$
Rightarrow
$$
$$
begin{align*}
-dfrac{3}{2}x+9&=dfrac{3}{2}x-3 tag{ add $ dfrac{3}{2}x$ to the each side}\
9&=3x-3tag{ add $3$ to the each side}\
12&=3xtag{ divide each side by $3$}\
x&=4
end{align*}
$$
Now, put $x=3$ into $y=-dfrac{3}{2}x+9$ and solve for $y$.
$$
begin{align*}
y&=-dfrac{3}{2}(4)+9\
y&=-dfrac{4}{2}(3)+9\
y&=-6+9\
y&=3
end{align*}
$$
Therefore, the intersection point is $(4,3)$.
$bullet$ Finding intersection point of $y=-dfrac{3}{2}x+9$ and $y=dfrac{3}{2}x+3$
$$
begin{align*}
-dfrac{3}{2}x+9&=dfrac{3}{2}x+3 tag{ add $ dfrac{3}{2}x$ to the each side}\
9&=3x+3tag{ subtract $3$ from the each side}\
6&=3xtag{ divide each side by $3$}\
x&=2
end{align*}
$$
Now, put $x=2$ into $y=-dfrac{3}{2}x+9$ and solve for $y$.
$$
begin{align*}
y&=-dfrac{3}{2}(2)+9\
y&=6
end{align*}
$$
Therefore, the intersection point is $(2,6)$.
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$
is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
$bullet$ The legth of the side with given end points $(0,3)$ and $(2,6)$ will be
$$
begin{align*}
text{length}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(2-0)^2+(6-3)^2}\
&=sqrt{(2)^2+(3)^2}\
&=sqrt{4+9}\
&=sqrt{13}
end{align*}
$$
$bullet$ The legth of the side with given end points $(2,6)$ and $(4,3)$ will be
$$
begin{align*}
text{length}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(4-2)^2+(3-6)^2}\
&=sqrt{(2)^2+(-3)^2}\
&=sqrt{13}
end{align*}
$$
$bullet$ The legth of the side with given end points $(4,3)$ and $(2,0)$ will be
$$
begin{align*}
text{length}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(2-4)^2+(0-3)^2}\
&=sqrt{(-2)^2+(-3)^2}\
&=sqrt{13}
end{align*}
$$
$bullet$ The legth of the side with given end points $(0,3)$ and $(2,0)$ will be
$$
begin{align*}
text{length}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(2-0)^2+(0-3)^2}\
&=sqrt{(2)^2+(-3)^2}\
&=sqrt{13}
end{align*}
$$
We have $y=-dfrac{3}{2}+3$ and $y=dfrac{3}{2}+3$ as a pair of adjacent sides.
$Rightarrow$ $text{product of slopes}=-dfrac{3}{2}times dfrac{3}{2}=-dfrac{9}{4} ne -1$
Therefore, the given system of lines intersect to make a rhombus.
The perimeter of the rhombus will be the sum of the lengths of its all sides.
$$
begin{align*}
text{Perimeter}&=sqrt{13}+sqrt{13}+sqrt{13}+sqrt{13}\
&=4times sqrt{13}\
&=4times 3.605\
&=14.422
end{align*}
$$
We can follow the same procedure as we did above, for all the parts. repeating the same for each part will make this answers enormously long and this will not serve the purpose.
Although the graphs and answers for each part is attached below.
$textbf{(b)}$ The quadrilateral formed by given points is a trapezium. There is one pair of opposite sides which have equal slope and hence are parallel.
$textbf{(b)}$ The quadrilateral formed by given points is a Trapezium. There is one pair of opposite sides which have equal slope and hence are parallel.
$textbf{(c)}$ The quadrilateral $WXYZ$ has no special properties.
The midpoint of any segment with given endpoint coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{midpoint}(x,y)=left ( dfrac{x_1+x_2}{2} right),left (dfrac{y_1+y_2}{2} right)
$$
$textbf{(a)}$ Finding the midpoint of segment $AB$ with end point coordinates $A(5,2)$ and $B(11,4)$. Let $(x_1,y_1)=(5,2)$ and $(x_2,y_2)=(11,14)$
$Rightarrow$
$$
text{midpoint}_x=dfrac{5+11}{2}=8
$$
$$
text{midpoint}_y=dfrac{2+14}{2}=8
$$
Therefore, the coordinates of the midpoint of points $A$ are $B$ are $(8,8)$.
$textbf{(b)}$ Similarly, we can find the coordinates of the segment $CD$ with the endpoints $C(3,8)$ and $D(10,4)$.
$$
Rightarrow
$$
$$
text{midpoint}_x=dfrac{3+10}{2}=6.5.5
$$
$$
text{midpoint}_y=dfrac{8+4}{2}=6
$$
Therefore, the coordinates of the points $C$ and $D$ are $(6.5,6)$
$textbf{(b)}$ The coordinates of the midpoint of points $(3,8)$ are $(10,4)$ are $(6.5,6)$.
$Rightarrow$
Calculating $angle B$ in $Delta ABC$
$$
begin{align*}
36text{textdegree} +angle B+42text{textdegree} &=180text{textdegree}\
angle B&=(180-42-36) text{textdegree}\
angle B&=102 text{textdegree}
end{align*}
$$
Similarly, we can find $angle Z$ in $Delta XYZ$
$$
begin{align*}
42text{textdegree} +angle Z+102text{textdegree} &=180text{textdegree}\
angle Z&=(180-42-102) text{textdegree}\
angle Z&=36 text{textdegree}
end{align*}
$$
So we have all the three angles of the given traingle pair, congruent. But AAA rule is not a sufficient condition for the traingle congruence. We need to have atleast one congreuent side along with this information to prove the congruence. Therefore, the given triangles are not congruent.
$$
text{hypotenuse}=sqrt{text{base}^2+text{height}^2}
$$
$bullet$ Finding length of the side $FD$
$$
begin{align*}
FD&=sqrt{{FE}^2+{ED}^2}\
FD&=sqrt{3^2+4^2}\
FD&=sqrt{25}\
FD&=5
end{align*}
$$
$bullet$ Finding length of the side $UG$
$$
begin{align*}
BG&=sqrt{{BU}^2+{UG}^2}\
5&=sqrt{3^2+{UG}^2}tag{square each side}\
25&=9+UG^2\
16&=UG^2tag{take square root on each side}\
UG&=4
end{align*}
$$
We can see that all the three sides of the given triangles are congruent. Therefore, we can say that $Delta FED cong Delta BUG$. The flowchart is attached below.
$textbf{(b)}$ Congruent by SSS rule.
$textbf{(c)}$ Congruent by SSS/RH rule.
$textbf{(a)}$
$bullet$ Checking the point $X(0,15)$ into the equation $y=dfrac{1}{3}x+15$
$$
begin{align*}
y&=dfrac{1}{3}x+15\
(15)&=dfrac{1}{3}(0)+15\
15&=15tag{true always}
end{align*}
$$
Therefore, the point $X(0,15)$ lie on the given line.
$bullet$ Checking the point $Y(3,16)$ into the equation $y=dfrac{1}{3}x+15$
$$
begin{align*}
y&=dfrac{1}{3}x+15\
(16)&=dfrac{1}{3}(3)+15\
16&=1+15\
16&=16 tag{true}
end{align*}
$$
Therefore, the point $Y(3,16)$ lie on the given line.
$bullet$ Checking the point $Z(7,0)$ into the equation $y=dfrac{1}{3}x+15$
$$
begin{align*}
y&=dfrac{1}{3}x+15\
(0)&=dfrac{1}{3}(7)+15\
0&=dfrac{7}{3}+15\
0ne 17.334
end{align*}
$$
We can see that point $Z(7,0)$ does not satisfice the line $y=dfrac{1}{3}x+15$. Therefore, the point $Z(7,0)$ does not lie on the given line.
$bullet$ Checking the point $X(0,15)$ into the equation $y-16=-4(x-3)$
$$
begin{align*}
y-16&=-4(x-3)\
(0)-16&=-4((15)-3)\
-16&=-4(12)\
-16ne -48
end{align*}
$$
We can see that point $X(0,15)$ does not satisfice the line $y-16=-4(x-3)$. Therefore, the point $X(0,15)$ lie on the given line.
$bullet$ Checking the point $Y(3,16)$ into the equation $y-16=-4(x-3)$
$$
begin{align*}
y-16&=-4(x-3)\
(16)-16&=-4((3)-3)\
0&=-4(0)\
0&=0tag{true always}
end{align*}
$$
Therefore, the point $Y(3,16)$ lie on the given line $y-16=-4(x-3)$.
$bullet$ Checking the point $Z(7,0)$ into the equation $y-16=-4(x-3)$
$$
begin{align*}
y-16&=-4(x-3)\
(0)-16&=-4((7)-3)\
-16&=-4(4)\
-16&=-16tag{true always}
end{align*}
$$
Therefore, the point $Z(7,0)$ lie on the given line $y-16=-4(x-3)$.
$textbf{(b)}$ The points $Y(3,16)$ and $Z(7,0)$ satisfice the equation $y-16=-4(x-3)$
Slope of a line which passes through a pair of points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
$bullet$ Finding slope of the Side $AB$
We are given the end points $A(2,3)$ and $B(6,6)$. Let $(x_1,y_1)=(2,3)$ and $(x_2,y_2)=(6,6)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{6-3}{6-2}\
&=dfrac{3}{4}
end{align*}
$$
$bullet$ Finding slope of the Side $AC$
We are given the end points $A(2,3)$ and $C(8,-5)$. Let $(x_1,y_1)=(2,3)$ and $(x_2,y_2)=(8,-5)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{-5-3}{8-2}\
&=dfrac{-8}{6}\
&=-dfrac{4}{3}
end{align*}
$$
Now, The product of the slopes of sides $AB$ and $AC$ is given by
$$
dfrac{3}{4}times -dfrac{4}{3}=-1
$$
We can see that their product of slopes is equal to $-1$ and hence sides $AB$ and $AC$ are perpendicular and therefore, $mangle A=90text{textdegree}$.
So, we can say that $Delta ABC$ is a right triangle.
$$
text{Isosceles triangle} rightarrow text{Two equal sides}
$$
$$
text{Equilateral triangle} rightarrow text{Three equal sides}
$$
$bullet$ Calculating the side length of $BC’$
The distance between any two points with given coordinates $(x_1,y_1)$ and $(x_2,y_2)$
is given by
$$
text{Distance}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
The legth of the side $BC’$ with given end points $B(6,6)$ and C’$(8,-5)$ will be
$$
begin{align*}
text{length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(8-6)^2+(6-(-5))^2}\
&=sqrt{(2)^2+(11)^2}\
&=sqrt{4+121}\
&=sqrt{125}\
&=5sqrt{5}
end{align*}
$$
$bullet$ Calculating the side length of $BB’$
The legth of the side $BC’$ with given end points $B(6,6)$ and B’$(-2,0)$ will be
$$
begin{align*}
text{length}_{AB}&=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\
&=sqrt{(6-(-2))^2+(6-0)^2}\
&=sqrt{(8)^2+(6)^2}\
&=sqrt{64+36}\
&=sqrt{100}\
&=10
end{align*}
$$
We can see that the side length of $BB’$ and sides $BC’/B’C’$ are different. Therefore, the $Delta BB’C’$ has only two equal sides and hence it is an Isosceles triangle.
$textbf{(b)}$ $Delta BB’C’$ has only two equal sides and hence it is an Isosceles triangle.
Assume number of boy $x$
Assume number of girl is $y$
$$
color{#4257b2} 5x+3y=175 x+y=45
$$
Multiply the second equ. by $3$ to get $3x+3y=135$
Using elimination property for the new equations as follows:
$$
(5x-3x)+(3y-3y)=(175-135) 2x=40
$$
Divide both of sides by $4$ as follows:
$$
x=dfrac{40}{2} x=20
$$
Substitution the value of $x=20$ for first equation as follows:
$$
(5cdot20)+3y=175 100+3y=175 3y=175-100
$$
$$
3y=75 y=-dfrac{75}{3} y=25
$$
Number of boys is $20$ boys. Number of girls is $25$ girls.
text{color{Brown}Number of boys is $20$ boys. Number of girls is $25$ girls.}
$$
$$a=dfrac{(sum y)(sum x^2)-(sum x)(sum xy)}{n(sum x^2)-(sum x)^2}$$\
$$b=dfrac{n(sum xy)-(sum x)(sum y)}{n(sum x^2)-(sum x)^2}$$
In the terms of $a$ and $b$ the LSRL equation is given by $$y=bx+a$$
The table of values is attached below.\
begin{tabular}{ |p{1.5cm}|p{2cm}|p{2cm}|p{1.5cm}|p{1.5cm}|p{1.5cm}| }
hline
Serial & $VO_2$max (ml/kg/min) $(x)$ & Power (watts) $(y)$ &$xy$ & $x^2$ & $y^2$\
hline
1 & 54 & 292 &15768 & 2916 & 85264\
hline
2& 51 & 362 &18462 & 2601 & 131044\
hline
3 & 49& 280 &13720 & 2401 & 78400\
hline
4 & 43 &293 &12599 & 1849 & 85849\
hline
5 & 53 & 280 &14840 & 2809 & 78400\
hline
6 & 59 & 413 &24367 & 3481 & 170569\
hline
7 & 64 & 358 &22912 & 4096 & 128164\
hline
8 & 58 & 293 &16994 & 3364 & 85849\
hline
9 & 56 & 342 &19152 & 3136 & 116964\
hline
10 & 55 & 335 &18425 & 3025 & 112225\
hline
$sum$ & 542 & 3248 &177239& 29678 & 1072728\
hline
end{tabular}\
Now, we need to calculate the values of $a$ and $b$ by using the values from the table above.
begin{align*}
a&=dfrac{(sum y)(sum x^2)-(sum x)(sum xy)}{n(sum x^2)-(sum x)^2}\
a&=dfrac{(3248)(29678)-(542)(177239)}{10(29678)-(542)^2}\
a&=dfrac{96394144-96063538}{296780-293764}\
a&=dfrac{330606}{3016}\
a&=109.6173\
a&=109.62tag{On estimating }
end{align*}
begin{align*}
b&=dfrac{n(sum xy)-(sum x)(sum y)}{n(sum x^2)-(sum x)^2}\
b&=dfrac{10(177239)-(542)(3248)}{10(29678)-(542)^2}\
b&=dfrac{1772390-1760416}{296780-293764}\
b&=dfrac{11974}{3016}\
b&=3.970159\
b&=3.9702tag{On estimating }
end{align*}
$$
Therefore, After putting $a=109.62$ and $b=3.9702$, the final equation of LSRL becomes
$$
boxed{y=3.9702x+109.62}
$$
$$
begin{align*}
y&=3.9702x+109.62\
y&=3.9702(43)+109.62\
y&=170.7186+109.62\
&boxed{y=280.34 text{ watts}}
end{align*}
$$
Therefore, the predicted power of the cyclist with $VO_2$max equal to 43 ml/kg/min will be 280.34 watts.
$textbf{(c)}$ The residual is defined as
$$
text{residual}=text{actual value}-text{predicted value}
$$
The actual value corresponding to $VO_2$max equal to 43 ml/kg/min is given 293 watts. We have calculated the predicted value from the LSRL as $280.34$
$Rightarrow$
$$
text{residual}=293-280.34=12.66
$$
The value of $rapprox 0.52$ shows that there is a positive correlation between the $VO_2$max value and the power which means when one of the variable increases, then the other variable also increases and varies similarly for the decrease.
The value of $r$ is not very significant (not very close to 1) and hence the association is not linear.
$textbf{(e)}$
$bullet$The association is positive which can be explained by the value of $r=0.52$
$bullet$ The direction is positive in this context which can be explained by its positive value of the slope, which is $text{slope}=3.9702$
$bullet$ The strength of this data can be predicted by finding the value of $R-squared$ value which is also called the coefficient of determination $(R^2)$.
$$
R^2=r^2=0.52^2=0.2704
$$
The value $R^2=0.27$ shows that the strength is weak and only 27 percent variation in the Power can be predicted by the value of $VO_2$max and rest variation is dependent on the other factors.
$textbf{(b)}$ 280.34 watts.
$textbf{(c)}$ 12.66
$textbf{(d)}$ The association is positive but not linear.
$textbf{(e)}$ The association is positive with $r=0.52$, the direction is positive with the value of slope equal to $3.9702$ and the strength is weak with $R^2=0.27$

