
All Solutions
Page 247: Questions
Every month thereafter, each pair of rabbits has two babies. Let $r(n)$ represents the number of rabbits in $n^text{th}$ month then the situation can be represented by the equation as shown below.
begin{align*}
r(0)&=2\
r(1)&=2times t(0)= 2times 2=2^2=2^{1+1}\
r(2)&=2times t(1)= 2times 2^2=2^3=2^{2+1}\
r(3)&=2times t(2)= 2times 2^3=2^4=2^{3+1}\
r(n)&=2times t(n-1)=2times 2^{n}=2^{n+1}
end{align*}
Therefore, the number of rabbits at the end of $n^text{th}$ month is given by the equation
$$boxed{r(n)=2^{n+1}}$$
$bullet$ The number of rabbits Lenny and George will have after 12 months can be found out by putting $n=12$ in the equation obtained above.
begin{align*}
r(n)&=2^{n+1}\
r(12)&=2^{12+1}\
r(12)&=2^{13}\
r(12)&=8192
end{align*}\
$bullet$ The pattern grows such as the number becomes two times of whatever the number of rabbits in the last month.\
The table for the growth is shown below where $n$ represents the number of months and $r(n)$ represents the number of rabbits.\\
begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}| }
hline
$n$ &0 &1&2&3&4&n \
hline
$r(n)$ &2&4&8&16&32&$2^{n+1}$\
hline
end{tabular}
$bullet$ This can be compared to any other pattern which grows two times at the end of each month and with the starting number is 2.
Most of the pattern we investigated earlier were linear and grew with the constant number but this pattern grows non linearly.
$$
r(n)=2^{n+1}
$$
For detailed explanation of each part see inside.
The number of rabbits at the end of $3^text{th}$ month is 16.
The table for the growth is shown below where $n$ represents the number of months and $r(n)$ represents the number of rabbits.\\
begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}| }
hline
$n$ &0 &1&2&3&4&5&6&n \
hline
$r(n)$ &2&4&8&16&32&64&128&$2^{n+1}$\
hline
end{tabular}\\
The pattern grows such as the number becomes two times of whatever the number of rabbits in the last month.\\
textbf{(c)} Let $r(n)$ represents the number of rabbits in $n^text{th}$ month then the situation can be represented by the equation as shown below.
begin{align*}
r(0)&=2\
r(1)&=2times t(0)= 2times 2=2^2=2^{1+1}\
r(2)&=2times t(1)= 2times 2^2=2^3=2^{2+1}\
r(3)&=2times t(2)= 2times 2^3=2^4=2^{3+1}\
r(n)&=2times t(n-1)=2times 2^{n}=2^{n+1}
end{align*}
Therefore, the number of rabbits at the end of $n^text{th}$ month is given by the equation
$$boxed{r(n)=2^{n+1}}$$
Hence,the number of rabbits Lenny and George will have after 12 months can be found out by putting $n=12$ in the equation obtained above.
begin{align*}
r(n)&=2^{n+1}\
r(12)&=2^{12+1}\
r(12)&=2^{13}\
&boxed{r(12)=8192}
end{align*}\
textbf{(d)} Most of the pattern we investigated earlier were linear and grew with the constant number but this pattern grows non linearly.\
$textbf{(b)}$ The pattern grows such as the number becomes two times of whatever the number of rabbits in the last month.
$textbf{(c)}$ 8192
$textbf{(d)}$ Most of the pattern we investigated earlier were linear and grew with the constant number but this pattern grows non linearly.
$bullet$ Case 2:\\
begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}| }
hline
$n$ &0 &1&2&3&4&5 \
hline
$r(n)$ &10&20&40&80&160&320\
hline
end{tabular}\\
$bullet$ Case 3:\\
begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}| }
hline
$n$ &0 &1&2&3&4&5 \
hline
$r(n)$ &2&8&32&128&512&2048\
hline
end{tabular}\\
$bullet$ Case 4:\\
begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}| }
hline
$n$ &0 &1&2&3&4&5 \
hline
$r(n)$ &2&12&72&432&2592&15552\
hline
end{tabular}\\
Therefore, a higher growth pattern will yield largest population rather than higher starting number of rabbits (if it is not very large starting value).\
Let $r(n)$ represents the number of rabbits in $n^text{th}$ month then the situation can be represented by the equation as shown below.
$$
begin{align*}
r(0)&=10=2times 5\
r(1)&=2times t(0)= 2times 2times 5= 2^2 times 5=2^{1+1}times 5\
r(2)&=2times t(1)= 2times 2^2 times 5=2^3times 5=2^{2+1}times 5\
r(n)&=2times t(n-1)=2times 2^{n}times 5 =2^{n+1}times 5
end{align*}
$$
Therefore, the number of rabbits at the end of $n^text{th}$ month is given by the equation
$$
boxed{r(n)=2^{n+1}times 5}
$$
Hence,the number of rabbits Lenny and George will have after 12 months can be found out by putting $n=12$ in the equation obtained above.
$$
begin{align*}
r(n)&=2^{n+1}times 5\
r(12)&=2^{12+1}times 5\
r(12)&=2^{13}times 5\
&boxed{r(12)=40960}
end{align*}
$$
Let $r(n)$ represents the number of rabbits in $n^text{th}$ month then the situation can be represented by the equation as shown below.
$$
begin{align*}
r(0)&=2\
r(1)&=r(0)times 4= 2times 4= 2times 4^1\
r(2)&=r(1)times 4= 2times 4^1 times 4= 2times 4^2\
r(n)&=r(n-1)times 4= 2times 4^(n-1) times 4= 2times 4^n\
end{align*}
$$
Therefore, the number of rabbits at the end of $n^text{th}$ month is given by the equation
$$
boxed{r(n)=2times 4^n }
$$
Hence,the number of rabbits Lenny and George will have after 12 months can be found out by putting $n=12$ in the equation obtained above.
$$
begin{align*}
r(n)&=2times 4^n\
r(12)&=2times 4^12\
r(12)&=2times 16777216\
&boxed{r(12)=33554432}
end{align*}
$$
Let $r(n)$ represents the number of rabbits in $n^text{th}$ month then the situation can be represented by the equation as shown below.
$$
begin{align*}
r(0)&=2\
r(1)&=r(0)times 6= 2times 6= 2times 6^1\
r(2)&=r(1)times 6= 2times 6^1 times 6= 2times 6^2\
r(n)&=r(n-1)times 6= 2times 6^(n-1) times 6= 2times 6^n\
end{align*}
$$
Therefore, the number of rabbits at the end of $n^text{th}$ month is given by the equation
$$
boxed{r(n)=2times 6^n }
$$
Hence,the number of rabbits Lenny and George will have after 12 months can be found out by putting $n=12$ in the equation obtained above.
$$
begin{align*}
r(n)&=2times 6^n\
r(12)&=2times 6^12\
r(12)&=2times 2176782336\
&boxed{r(12)=4353564672}
end{align*}
$$
$textbf{(b)}$ Case 2: $rightarrow$ 40960
Case 3: $rightarrow$ 33554432
Case 4: $rightarrow$ 4353564672
$textbf{(b)}$ The graph for case 1: is attached below.
The graph is growing exponentially with the equation of the function
$$
r(n)=2^{n+1}
$$
where, $r(n)$ is the number of rabbits and $n$ is the number of months.
The range of the graph is discrete points which are $(2,4,8,16,32,64,128,cdots)$
$bullet$ The graph is discrete as we are assuming that number are multiplying at the end of each month not at every point of time.
$bullet$ Yes, it is a discrete function, as corresponding to a value of input there is only single value of output.
$textbf{(b)}$ The graph is growing exponentially with the equation of the function
$$
r(n)=2^{n+1}
$$
where, $r(n)$ is the number of rabbits and $n$ is the number of months.
$textbf{(c)}$ The domain for the graph is whole numbers $(0,1,2,3,4,cdots)$
The range of the graph is discrete points which are $(2,4,8,16,32,64,128,cdots)$
The graph is discrete as we are assuming that number are multiplying at the end of each month not at every point of time.
Yes, it is a discrete function, as corresponding to a value of input there is only single value of output.
We can observe if it has vertical or horizontal asymptotes, holes and also end behavior as well.
Also, we can investigate if it is continuous or no, what is its domain and range.
begin{align*}
r(0)&=4\
r(1)&=12=3times 4=3times r(0)=3^1times 4 \
r(2)&=36=3times 12=3times r(1)=3^2times 4 \
r(n)&=3times r(n-1)=3^{n}times 4
end{align*}
Therefore, from the starting number of 4 rabbits we can find the number of rabbits after any $n^text{th}$ month by the equation $$boxed{r(n)=3^{n}times 4 } $$
For example, Number of rabbits in the $3^text{rd}$ month is given by
begin{align*}
r(n)&=3^{n}times 4 \
r(3)&=3^{3}times 4 \
r(3)&=27times 4 \
r(3)&=108
end{align*}
The table of other values is included below.
begin{center}
begin{tabular}{ |p{2cm}|p{2cm}| }
hline
Months & Rabbits \
hline
0 & 4 \
hline
1 & 12 \
hline
2 & 36 \
hline
3&108\
hline
4&324\
hline
end{tabular}
end{center}
begin{align*}
r(0)&=6\
r(2)&=24= 4times 6=2^2times 6 \
r(4)&=96=16times 6=2^4times 6 \
r(n)&=2^n times 6
end{align*}
Therefore, from the starting number of 6 rabbits we can find the number of rabbits after any $n^text{th}$ month by the equation $$boxed{r(n)=2^n times 6 } $$
For example, Number of rabbits in the $1^text{st}$ month is given by
begin{align*}
r(n)&=2^n times 6 \
r(1)&=2^1 times 6 \
r(1)&=2times 6\
r(1)&=12
end{align*}
Similarly, the number of rabbits in the $3^text{rd}$ month is given by
begin{align*}
r(n)&=2^n times 6 \
r(3)&=2^3 times 6 \
r(3)&=8times 6\
r(3)&=48
end{align*}
The table of other values is included below.
begin{center}
begin{tabular}{ |p{2cm}|p{2cm}| }
hline
Months & Rabbits \
hline
0 & 6 \
hline
1 & 12 \
hline
2 & 24 \
hline
3&48\
hline
4&96\
hline
end{tabular}
end{center}
$$
r(n)=3^{n}times 4
$$
$textbf{(b)}$ From the starting number of 6 rabbits, we can find the number of rabbits after any $n^text{th}$ month by the equation
$$
r(n)=2^{n}times 6
$$
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Lets choose the points $(3,4)$ and $(3,2)$. Let $(x_1,y_1)=(3,4)$ and $(x_2,y_2)=(3,2)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{2-4}{3-3}\
&=dfrac{-2}{0}\
&approx infty
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $infty$ passing through a point $(3,4)$ is given by
$$
begin{align*}
y-4&= infty cdot (x-3)\
dfrac{y-4}{infty}&= dfrac{infty}{infty}cdot (x-3)\
0&=1cdot (x-3)\
0&=x-3\
boxed{x=3}
end{align*}
$$
Therefore, the equation of line is is $x=3$ and coordinates of the other points on it are marked in the red in the graph attached below.
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Lets choose the points $(-3,-1)$ and $(1,-1)$. Let $(x_1,y_1)=(-3,-1)$ and $(x_2,y_2)=(1,-1)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{-1-(-1)}{1-(-3)}\
&=dfrac{-1+1}{1+3}\
&=dfrac{0}{4}\
&=0
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $0$ passing through a point $(-3,-1)$ is given by
$$
begin{align*}
y-(-1)&= 0 cdot (x-(-3))\
y+1&=0\
y&=-1\
boxed{y=-1}
end{align*}
$$
Therefore, the equation of line is is $y=-1$ and coordinates of the other points on it are marked in the red in the graph attached below.
The graph is attached below.
$textbf{(b)}$ $y=-1$
$textbf{(c)}$ $x=0$
Now, when we put $x=1$ into the $g(x)$ function we get
$$
begin{align*}
g(x)&=dfrac{x+2}{x-1}\
g(1)&=dfrac{1+2}{1-1}\
g(1)&=dfrac{3}{0}\
g(1)&=text{not defined}
end{align*}
$$
Therefore, $x=1$ cannot be in the domain of the function $g(x)$.
$$
begin{align*}
&3.295text{ kg} cdot( dfrac{1000 text{ g}}{1 text{kg}})\
&=3.295 1 cdot 1000 text{ g} cdot ( dfrac{1 text{ kg}}{1 text{ kg}})\
&=3.295cdot 1000 text { g}\
&=3295 text { g}
end{align*}
$$
Given that there are 28.3 grams in 1 ounce. Therefore, 3295 grams can be converted into ounce as shown below
$$
begin{align*}
&3295 text{ g} cdot dfrac{ 1 text{ ounce}}{28.3 text{ g}}\
&=dfrac{3295}{28.3}cdot dfrac{text{ g}}{text{ g}}cdot text{ ounce}\
&=dfrac{3295}{28.3}cdot text{ ounce}\
&=116.43 text{ ounce}
end{align*}
$$
Now, as we know that there are 16 ounces in 1 pound. Therefore, 116.43 ounces can be rewritten as
$$
dfrac{116.43}{16}=7. 2768text{ pounds}
$$
This can be also written as 7 pounds and $0.2768times 16=4.4288text { ounces}$
Hence, 3.295 kg is equivalent to 7 pounds and 4.4288 ounces.
$$
begin{align*}
A(1,1)&rightarrow A'(-1,1)\
B(-1,-1)&rightarrow B'(1,-1)\
C(4,-1)&rightarrow C'(-4,-1)
end{align*}
$$
Therefore, the coordinates of the vertex points of $Delta$A’B’C’ are $A'(-1,1)$, $B'(1,-1)$ and $C'(-4,-1)$.
The resultant figure $Delta$A’B’C’ is the result of reflection of $Delta$ABC across the line $x=0$.
$$
begin{align*}
A(1,1)&rightarrow A”(5,6)\
B(-1,-1)&rightarrow B”(3,4)\
C(4,-1)&rightarrow C”(8,4)
end{align*}
$$
$$
begin{align*}
A(1,1)&rightarrow A'(-1,1)\
B(-1,-1)&rightarrow B'(1,-1)\
C(4,-1)&rightarrow C'(-4,-1)
end{align*}
$$
$textbf{(b)}$ The coordinates of the resultant figure $Delta$A”B”C” are
$$
begin{align*}
A(1,1)&rightarrow A”(5,6)\
B(-1,-1)&rightarrow B”(3,4)\
C(4,-1)&rightarrow C”(8,4)
end{align*}
$$
In the second sentence, one more variable which can be the actual cause is $textbf{smoking cigarettes}$.
textbf{(b)}
begin{center}
begin{tabular}{|p{3cm}|p{4cm}|}
hline
Number of days & Number of bacteria\
hline
0 & 1000\
hline
1 & 2000\
hline
2 &4000\
hline
3 &8000\
hline
n & $2^ntimes 1000$\
hline
end{tabular}
end{center}
The points are connected on the graph to show the shape of the curve . It does imply that the function takes all those values. Yes, it is a Discrete function.
$textbf{(b)}$ The number of bacteria on $n^text{th} text{ day is }2^ntimes 1000$
$textbf{(c)}$ The graph is exponential which has domain as whole numbers $(0,1,2,3,4,cdots)$ and the range is the discrete points $(1000,2000,4000,8000,cdots)$
The points are connected on the graph to show the shape of the curve . It does imply that the function takes all those values. Yes, it is a Discrete function.
{color{#4257b2}text{a)}}
$$
$$
begin{align*}
frac{5^{723}}{5^{721}}& {=}quad : 5^{723-721}\
&=5^2 \
&={color{#c34632}25}
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad frac{x^a}{x^b}:=:x^{a-b}
$$
$$
text{ }
$$
{color{#4257b2}text{b)}}
$$
$$
begin{align*}
frac{3^{300}}{3^{249}}& {=}quad : 3^{300-249}\
&={color{#c34632}3^{51}}
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad frac{x^a}{x^b}:=:x^{a-b}
$$
$$
text{ }
$$
{color{#4257b2}text{c)}}
$$
$$
begin{align*}
left(frac{34^3}{3^{-2}cdot :4^{-7}}right)^0& {=}quad : color{#c34632}1\
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Apply:rule}:a^0=1,:ane :0
$$
$$
text{ }
$$
{color{#4257b2}text{d)}}
$$
$$
begin{align*}
left(frac{4cdot :10^3}{10^{-2}}right)^2& {=}quad : left(4cdot :10^5right)^2\
&=4^2left(10^5right)^2 \
&=color{#c34632}4^2cdot :10^{10} \
end{align*}
$$
color{#4257b2} text{ a) }25
$$
$$
color{#4257b2} text{ b) }3^{51}
$$
$$
color{#4257b2}text{ c) }1
$$
$$
color{#4257b2}text{ d) }4^2*10^{10}
$$
$$
(a+b)^2=a^2+2ab+b^2
$$
But during solving for $(x+4)^2$ she wrote $(x+4)^2=x^2+16$ which is wrong. Also, in the right side of equation, while opening $(x-1)^2$ she wrote $(x-1)^2=x^2+1$.
The correct solution is shown below
$$
begin{align*}
(x + 4)^2 -2 x -5 &= (x -1 )^2\
(x^2+8x+16)-2x-5&=x^2-2x+1\
x^2+6x+11 &=x^2-2x+1\
6x+2x&=1-11\
8x&=-10\
x&=-dfrac{10}{8}\
x&=-dfrac{5}{4}\
end{align*}
$$
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $-2$ passing through a point $(0,7)$ is given by
$$
begin{align*}
y&-7=-2cdot (x-0)\
y&-7=-2x\
&boxed{y=-2x+7}
end{align*}
$$
$textbf{(b)}$ The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $-dfrac{3}{2}$ passing through a point $(4,0)$ is given by
$$
begin{align*}
y-0&=-dfrac{3}{2}cdot (x-4)\
y&=-dfrac{3}{2}cdot x + (-dfrac{3}{2} cdot -4) \
y&=-dfrac{3}{2}cdot x +dfrac{12}{2}\
&boxed{y=-dfrac{3}{2}cdot x+6}
end{align*}
$$
$$
begin{align*}
mtimes -dfrac{3}{2}&=-1\
m&=dfrac{-1}{(-dfrac{3}{2})}\
m&=dfrac{-1times 2}{-3}\
m&=dfrac{2}{3}
end{align*}
$$
Therefore, the equation of a line of slope $dfrac{2}{3}$ passing through a point $(4,0)$ is given by
$$
begin{align*}
y-0&=dfrac{2}{3}cdot (x-4)\
y&=dfrac{2}{3}cdot x + (dfrac{2}{3} cdot -4) \
&boxed{y=dfrac{2}{3}cdot x -dfrac{8}{3}}
end{align*}
$$
$textbf{(b)}$ $y=-dfrac{3}{2}cdot x+6$
$textbf{(c)}$ $y=dfrac{2}{3}cdot x -dfrac{8}{3}$
$$
text{Area}= dfrac{3}{2}+6+6 = dfrac{27}{2} text { unit}^2
$$
$textbf{(c)}$ $dfrac{27}{2} text{ unit}^2$
$$
begin{align*}
&dfrac{1}{4}k^5-3k^3+k^2-k\
&=dfrac{1}{4}(2)^5-3(2)^3+(2)^2-(2)\
&=dfrac{1}{4}(32)-3(8)+(4)-(2)\
&=8-24+2\
&=boxed{-14}
end{align*}
$$
$textbf{(a)}$ Tennis balls rebound approximately 111 cm when dropped from 200 cm.
Therefore, when dropped from 1 cm it will rebound $dfrac{111}{200}=0.555$ cm.
$textbf{(b)}$ Soccer balls rebound approximately 120 cm when dropped from 200 cm.
Therefore, when dropped from 1 cm it will rebound $dfrac{120}{200}=0.6$ cm.
$textbf{(c)}$ Basketballs rebound approximately 53.5 inches when dropped from 72 inches. 1 inch is equivalent to 2.54 cm. Therefore 53.5 inches= 135.89 cm and 72 inches= 182.88 cm.
Therefore, when a basketball is dropped from 1 cm it will rebound $dfrac{135.89}{182.88}=0.743$ cm.
$textbf{(d)}$ Squash balls rebound approximately 29 .5 inches when dropped from 100 inches. 29.5 inches= 74.93 cm and 100 inches= 254 cm.
Therefore, when a basketball is dropped from 1 cm it will rebound $dfrac{74.93}{254}=0.295$ cm.
Comparing the rebound height of each ball when it is dropped from 1 cm, we see that basketball rebounds highest of all which is 0.743 cm. Therefore, basketball is the bounciest of all.
Basketball is the bounciest among the listed balls.
All it can be measured by the one team member and the other can spread data in the table.
Rebound height $rightarrow$ Dependent variable
Dropping height $rightarrow$ Independent variable
$textbf{(b)}$ The graph will be discrete as not all the values of height can be obtained by dropping the ball.
$textbf{(c)}$ The graph may vary according to different types of ball (re bouncing characteristics). But the line will always pass through origin as if the dropping height is 0 then the rebound height will also be 0.
$textbf{(d)}$ Some of the example lines are shown in the graph below. We can generalise that the rebound height is always less than the dropping height. Therefore, on the graph the lines obtained will always lie below the line drawn in red ($y=x$)
Also, the as negative height is not possible, so the line will not be valid for the negative values of any of the $x$ and $y$ variables.
Rebound height $rightarrow$ Dependent variable
Dropping height $rightarrow$ Independent variable
$textbf{(b)}$ The graph will be discrete as not all the values of height can be obtained by dropping the ball.
$textbf{(c)}$ The graph may vary according to different types of ball (re bouncing characteristics). But the line will always pass through origin as if the dropping height is 0 then the rebound height will also be 0.
$textbf{(d)}$ Some of the example lines are shown in the graph attached inside.
$bullet$ Rebound ratio is given by the slope of the line of the best fit.
$bullet$ In the general form equation of line which is given by $y=mx+c$. The $m$ represents the slope of line and hence, here in this context $m$ is equivalent to rebound ratio.
$bullet$ The rebound ratio which is equivalent to slope of the line of best fit can be calculated by choosing coordinates of any two set of points on the line as shown below.
$$
begin{align*}
text{Rebound ratio}&=dfrac{y_2-y_1}{x_2-x_1}\
&=dfrac{Delta y}{Delta x}
end{align*}
$$
$$
begin{align*}
2(x-2)&=-6tag{divide each side by 2}\
dfrac{2(x-2)}{2}&=dfrac{-6}{2}\
x-2&=-3tag{add 2 to each side}\
x-2+2&=-3+2\
&boxed{x=-1}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
2(x+1)+3&=3(x-1)tag{solve brackets using distributive property}\
2x+2+3&=3x-3tag{subtract $2x$ from each side}\
2x-2x+5&=3x-2x-3\
5&=x-3tag{add 3 to the each side}\
5+3&=x-3+3\
8&=xtag{interchange side}\
&boxed{x=8}
end{align*}
$$
$textbf{(b)}$ $x=8$
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we have given points as $(6,-8)$ and $(3,-4)$. Let $(x_1,y_1)=(3,-4)$ and $(x_2,y_2)=(6,-8)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{-8-(-4)}{6-3}\
&=dfrac{-8+4}{3}\
&=dfrac{-4}{3}
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $dfrac{-4}{3}$ passing through a point $(3,-4)$ is given by
$$
begin{align*}
y-(-4)&=dfrac{-4}{3}cdot (x-3)\
y+4&=dfrac{-4}{3}cdot x + dfrac{-4}{3}cdot (-3)\
y+4&=dfrac{-4}{3}cdot x +4 tag{subtract 4 from each side}\
y+4-4&=dfrac{-4}{3}cdot x +4-4\
&boxed{y=dfrac{-4}{3}cdot x}
end{align*}
$$
$$
begin{align*}
y&=-dfrac{4}{3}x\
(4)&=-dfrac{4}{3}(-3)\
4&=-1cdot dfrac{-3}{3}cdot 4\
4&=-1cdot -1 cdot 4\
4&=4tag{true always}
end{align*}
$$
The point $(-3,4)$ satisfies the line $y=-dfrac{4}{3}x$ and hence it lies on it.
$textbf{(b)}$ Yes, the point $(-3,4)$ lies on the line.
$Rightarrow$
$$
R^2=(-0.903)^2=0.8154
$$
The value of coefficient of determination ($R^2$) is $0.8154approx 0.81$ which signifies that the approximately 81 percent variation in fuel efficiency can be predicted by weight of the cars. Rest 19 percent variation is dependent on the other factors.
$textbf{(b)}$ The given equation is $y=49-8.4x$
The slope of this line represent the rate of change in the fuel efficiency (miles per gallon) of the car per thousands pound change in the weight of a car.
Here slope is negative which shows that if the weight of the car increases then the efficiency of the car will decrease.
$textbf{(b)}$
The slope of this line represent the rate of change in the fuel efficiency (miles per gallon) of the car per thousands pound change in the weight of a car.
Here slope is negative which shows that if the weight of the car increases then the efficiency of the car will decrease.
Let$w$represent the weight of the package in ounces, then the cost of sending a package via AAA Packages Plus is given by$ $text{Cost (via AAA)}= 5+0.25w$ $United Packages charges $2 plus $0.35 per ounce.Therefore,$ $text{Cost (via United)}= 2+0.35w$ $Given that, Molinari’s package would cost the same to mail using either service.$Rightarrow$5+0.25w=2+0.35w$$
$textbf{(b)}$ weight of the Molinari’s package can be found out by solving the final equation in the previous part.
$$
begin{align*}
5+0.25w&=2+0.35w\
5-2&=(0.35-0.25)w\
3&=0.1w\
w&=dfrac{3}{0.1}\
w&=3 times 10\
w&=30 text{ ounces}
end{align*}
$$
$textbf{(b)}$ 30 ounces.
begin{align*}
text{Time}&=dfrac{text{Distance}}{text{Speed}}\
Rightarrow text{Time}&=dfrac{24 text{blocks}}{1 text{block per minute}}\
&=boxed{24 text{ minute}}
end{align*}
Now, if she travels two blocks every minute the time to reach her friend’s house is given by
begin{align*}
text{Time}&=dfrac{24 text{blocks}}{2 text{block per minute}}\
&=boxed{12 text{ minute}}
end{align*}\
textbf{(b)}\
begin{tabular}{ |p{4cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}| }
hline
Speed (blocks per minute)&1&2&3&4&6&8&10&12&24 \
hline
Time to Get to Friend’s
House (minutes) &24&12&8&6&4&3&2.4&2&1\
hline
end{tabular}
The formula $text{Time}=dfrac{text{Distance}}{text{Speed}}$ explains it well.
$textbf{(d)}$ Yes, this is a proportional relationship as the formula $text{Time}=dfrac{text{Distance}}{text{Speed}}$ contains a unit power to the each terms.
$textbf{(c)}$ From the table we can see that time taken by her to reach her friend’s house decreases as Meredith increases her speed.
$textbf{(d)}$ Yes, this is a proportional relationship.
$$
begin{align*}
y &= 10times(12) – 8\
y&=120-8\
y&=112
end{align*}
$$
By solving the given equation, we got that the Figure 12 of this pattern contains 112 tiles whereas Kalil thinks there should be 108 tiles in it. Therefore, kalil is not correct.
$$
text{rebound ratio}=dfrac{120}{200}=0.6
$$
$textbf{(b)}$ No, the dropping height of the ball will not affect the ratio.
$textbf{(c)}$ For finding rebound height for any given dropping height we multiply the ratio with the dropping height.
As rebound ratio is given by
$$
text{rebound ratio}=dfrac{text{rebound height}}{text{dropping height}}
$$
$Rightarrow$
$$
text{rebound height}=text{rebound ratio} times text{dropping height}
$$
$textbf{(b)}$ No, the dropping height of the ball will not affect the ratio.
$$
textbf{(c)}text{rebound height}=text{rebound ratio} times text{dropping height}
$$
The rebound height after each bounce can be found by the formula
begin{align*}
text{RH}_n=200times ( dfrac{48}{100})^n
end{align*}
where, $text{RH}_n$ represents the rebound height after $n$ rebounds.\
begin{center}
begin{tabular}{|p{4cm}|p{3cm}|}
hline
Number of bounces &Rebound height\
hline
1&96\
hline
2&46.08\
hline
3&22.118\
hline
4&10.616\
hline
n& $200times ( dfrac{48}{100})^n$\
hline
end{tabular}
end{center}
Dependent variable $rightarrow$ Rebound height
$textbf{(c)}$ The graph of the predicted rebound heights is attached below.
$textbf{(d)}$ The graph is discrete as it is not possible to obtain all the values of rebounding heights via bouncing ball.
$textbf{(b)}$ Independent variable $rightarrow$ Dropping height
Dependent variable $rightarrow$ Rebound height
$textbf{(c)}$ The graph of the predicted rebound heights is attached below.
$textbf{(d)}$ The graph is discrete as it is not possible to obtain all the values of rebounding heights via bouncing ball.
$bullet$ Graph and model represents the model with some errors (negative residues) which is tolerable upto some extent.The negative residues between actual and predicted data signifies that the actual values of rebound height is smaller than the predicted height after every bounce
The model for successive bounces is not linear so we cannot use $y=mx+b$ to model the data. The data is also not quadratic since the bounces are never higher the the previous bounce. So, the model for the data is exponential.
$textbf{b.}$
The pattern of growth is that each successive bounce height is the previous bounce height multiplied by the same factor that is less than 1. This is the same as the rabbit problem where the factor that is being multiplied is greater than 1.
b. The pattern of growth is that each successive bounce height is the previous bounce height multiplied by the same factor that is less than 1.
$$
text{RH}_n=200(dfrac{48}{100})^n
$$
Therefore, the rebound height of ball after twelth bounce will be
$$
text{RH}_{12}=200(dfrac{48}{100})^{12}
$$
From the equation we can see, the rebound value will only become 0 when $n$ reaches to infinity which means that theoretically ball never stops. But, due to friction and air drag ball stops after some time.
An exponential function is reserved for high growth, but when we have decreasing, usually, it is linear realtionship.
$$
f(x)=ab^x
$$
Where $b>0$.
For $b=1$, this function is constant.
For $a>0$ and $b>1$, this function is increasing.
For $b<1$, this function is decreasing.
f(x)=ab^x
$$
To find the rebound ratio, divide the rebound height by the drop height. We do this for all data and then estimate:
$$
begin{align*}
dfrac{124}{150}&approx 0.83 & dfrac{83}{100}&= 0.83\
dfrac{59}{70}&approx 0.84 & dfrac{92}{110}&= 0.84\
dfrac{100}{120}&approx 0.83 & dfrac{33}{40}&= 0.83
end{align*}
$$
A good estimate for the rebound ratio for their ball is $text{textcolor{#c34632}{0.83}}$.
$textbf{b.}$
To find the rebound height, multiply the drop height by the rebound ratio:
$$
275text{ cm}cdot 0.83approx color{#c34632}228text{ cm}
$$
$textbf{c.}$
To find the drop height, divide the rebound height by the rebound ratio:
$$
dfrac{60text{ cm}}{0.83}approx color{#c34632}72text{ cm}
$$
$textbf{d.}$
In this case, the drop height is 200 m. To find the rebound height, multiply the drop height by the rebound ratio:
$$
200text{ m}cdot 0.83approx color{#c34632}166text{ m}
$$
$textbf{e.}$
Continue multiplying the drop height by the rebound ratio to find the required rebound heights:
$$
begin{align*}
&text{after the second bounce: }166text{ m}cdot 0.83approx color{#c34632}138text{ m}\
&text{after the third bounce: }138text{ m}cdot 0.83approx color{#c34632}115text{ m}
end{align*}
$$
b. about 228 cm
c. about 72 cm
d. about 166 cm
e. 138 m ; 115 m
$textbf{(a)}$ Given that the dropping height of the tennis ball is 10 feet. The rebound height of the ball can be found by multiplying the dropping height by rebound ratio as shown below.
$$
begin{align*}
text{rebound height}&=10times 0.555\
&=5.55 text{ feet}
end{align*}
$$
$textbf{(b)}$ For finding the rebound height after the second bounce, we consider the new dropping height as 5.55 feet and multiply it with the rebound ratio.
$$
begin{align*}
text{rebound height after second bounce}&=5.55times 0.555\
&=3.08 text{ feet}
end{align*}
$$
$textbf{(c)}$ Either we can keeps on multiplying rebound ratio five times as done above or we can put the $n=5$ in the general form equation, which is given by
$$
begin{align*}
text{rebound height}_n&=10times (0.555)^n\
text{rebound height}_5&=10times (0.555)^5\
&=10times0.0526\
&=0.526
end{align*}
$$
$textbf{(b)}$ $3.08$ feet
$textbf{(c)}$ $0.526$ feet
First we can consider the given variable $f(x)$ as output variable $y$.
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we can choose two points as $(3,4)$ and $(5,10)$. Let $(x_1,y_1)=(3,4)$ and $(x_2,y_2)=(5,10)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{10-4}{5-3}\
&=dfrac{6}{2}\
&=3
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $3$ passing through a point $(3,4)$ is given by
$$
begin{align*}
y-(4)&=3cdot (x-3)\
y-4&=3cdot x+3cdot (-3)\
y&=3cdot x-9+4\
y&=3cdot x-5
end{align*}
$$
Now, again replace the $y$ as $f(x)$ then the equation becomes
$$
boxed{f(x)=3cdot x-5}
$$
We can check the validity of the equation by putting any other point from the table and see if it satisfies the equation or not.
Lets check the validity of the equation for the point $(12,31)$
$$
begin{align*}
f(x)&=3cdot x-5\
31&=3cdot (12)-5\
31&=36-5\
31&=31tag{true always}
end{align*}
$$
Hence, our equation for the line is valid.
f(x)=3cdot x-5
$$
In the second sentence, one more variable which can be the actual cause are sugars.
$$
begin{align*}
dfrac{2x-8}{10}&=6tag{multiply each side by 10}\
(dfrac{2x-8}{10})cdot 10&=6cdot 10\
2x-8&=60tag{add 8 to the each side}\
2x-8+8&=60+8\
2x&=68tag{ divide each side by 2}\
dfrac{2x}{2}&=dfrac{68}{2}\
&boxed{x=34}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
9^x&=3^{40} tag{replace $9$ with $3^2$}\
(3^2)^x&=3^{40}tag{use $(a^m)^n=a^{mcdot n}$}\
3^{2 cdot x}&=3^40 tag{equate the powers as base is same}\
2x&=40tag{divide each side by 2}\
dfrac{2x}{2}&=dfrac{40}{2}\
&boxed{x=20}
end{align*}
$$
$textbf{(b)}$ $20$
(b) The resultant polygon is a rectangle.
The sequence generator multiplies the input by 3:
$$
begin{align*}
2cdot 3&=6\
6cdot 3&=18\
18cdot 3&=54
end{align*}
$$
$textbf{b.}$
By continuing to multiply the input by 3, as what we found the sequence generator does, the next two terms are:
$$
begin{align*}
54cdot 3&=color{#c34632}162\
162cdot 3&=color{#c34632}486
end{align*}
$$
$textbf{c.}$
The first term is 5 so the next four terms are:
$$
begin{align*}
5cdot 3&=color{#c34632}15\
15cdot 3&=color{#c34632}45\
45cdot 3&=color{#c34632}135\
135cdot 3&=color{#c34632}405
end{align*}
$$
b. 162 ; 486
c. 15, 45, 135, and 405
$textbf{(b)}$ For finding next two terms we consider starting input to next sequence generator is $162$ therefore, output for this will be
$$
162times 3 =486
$$
Now, 486 goes to the next sequence generator as input and hence output for this will be
$$
486times 3=1458
$$
Therefore, next two terms of the sequence are $486, 1485,cdots$
$textbf{(c)}$ The first four terms of the sequence can be found by multiplying each of the previous resultant term with 3 for the next term. Let $t(n)$ represent the $n^text{th}$ term of the sequence.
$$
begin{align*}
t(1)&=4\
t(2)&=t(1)times 4=4times 4=16\
t(3)&=t(2)times 4=16times 4=64\
t(4)&=t(3)times 4=64times 4=256\
t(5)&=t(4)times 4=256times 4=1024
end{align*}
$$
therefore, the next 4 terms of the sequence are $(16, 64, 256, 1024)$
$textbf{(b)}$ $86, 1485$
$textbf{(c)}$ The next 4 terms of the sequence are $(16, 64, 256, 1024)$
$textbf{a.}$
Each term is found by adding a constant number to the previous term which is 3:
$$
-4,-1,2,5,color{#c34632}8,11,14
$$
$textbf{b.}$
Each term is found by multiplying a constant number to the previous term which is 2:
$$
1.5,3,6,12,color{#c34632}24,48,96
$$
$textbf{c.}$
The terms of the sequence are the squares of the whole numbers:
$$
0^2,1^2,2^2,3^2,dots
$$
So, the next 3 terms are:
$$
0^2,1^2,2^2,3^2, 4^2,5^2,6^2
$$
or
$$
0,1,4,9, color{#c34632}16,25,36
$$
$textbf{d.}$
Each term is found by adding a constant number to the previous term which is 1.5:
$$
2,3.5, 5,6.5,color{#c34632}8,9.5, 11
$$
$textbf{e.}$
Starting from the third term, each term is found by adding the previous two terms:
$$
1,1,2,3,5,8,color{#c34632}13,21,34
$$
Each term is found by adding a constant number to the previous term which is $-2$:
$$
9,7,5,3,color{#c34632}1,-1,-3
$$
$textbf{g.}$
Each term is found by multiplying a constant number to the previous term which is $dfrac{1}{2}$:
$$
48,24,12,color{#c34632}6,3,dfrac{3}{2}
$$
$textbf{h.}$
Each term is found by multiplying a constant number to the previous term which is $dfrac{1}{3}$:
$$
27,9,3,1,color{#c34632}dfrac{1}{3}, dfrac{1}{9},dfrac{1}{27}
$$
$textbf{i.}$
The terms of the sequence are the squares of the integers from $-2$, multiplied by 2:
$$
2(-2)^2, 2(-1)^2, 2(0)^2, 2(1)^2, 2(2)^2, 2(3)^2,dots
$$
So, the next 3 terms are:
$$
2(-2)^2, 2(-1)^2, 2(0)^2, 2(1)^2, 2(2)^2, 2(3)^2, 2(4)^2, 2(5)^2, 2(6)^2
$$
or
$$
8,2,0,2,8,18,color{#c34632}32,50,72
$$
$textbf{j.}$
Each term is found by multiplying a constant number to the previous term which is $2$:
$$
dfrac{5}{4},dfrac{5}{2},5,10,color{#c34632}20,40,80
$$
Based on the results, the following sequences belong to the same family where you add a constant number to find the next term:
a, d, and f
The following sequences belong to the same family where you multiply a constant number to find the next term:
b, g, h, and j
The following sequences belong to the same family where you square a number:
c and i
Only sequence e does not belong to any kind of family.
(2)
The next terms were already given above (which should be written on the strips).
(3) and (4)
The Resource Page for (3) is a table and a graph for (4) which is shown below. All sequences should be discrete (that is, just points), since we only took natural numbers from $n=1$.
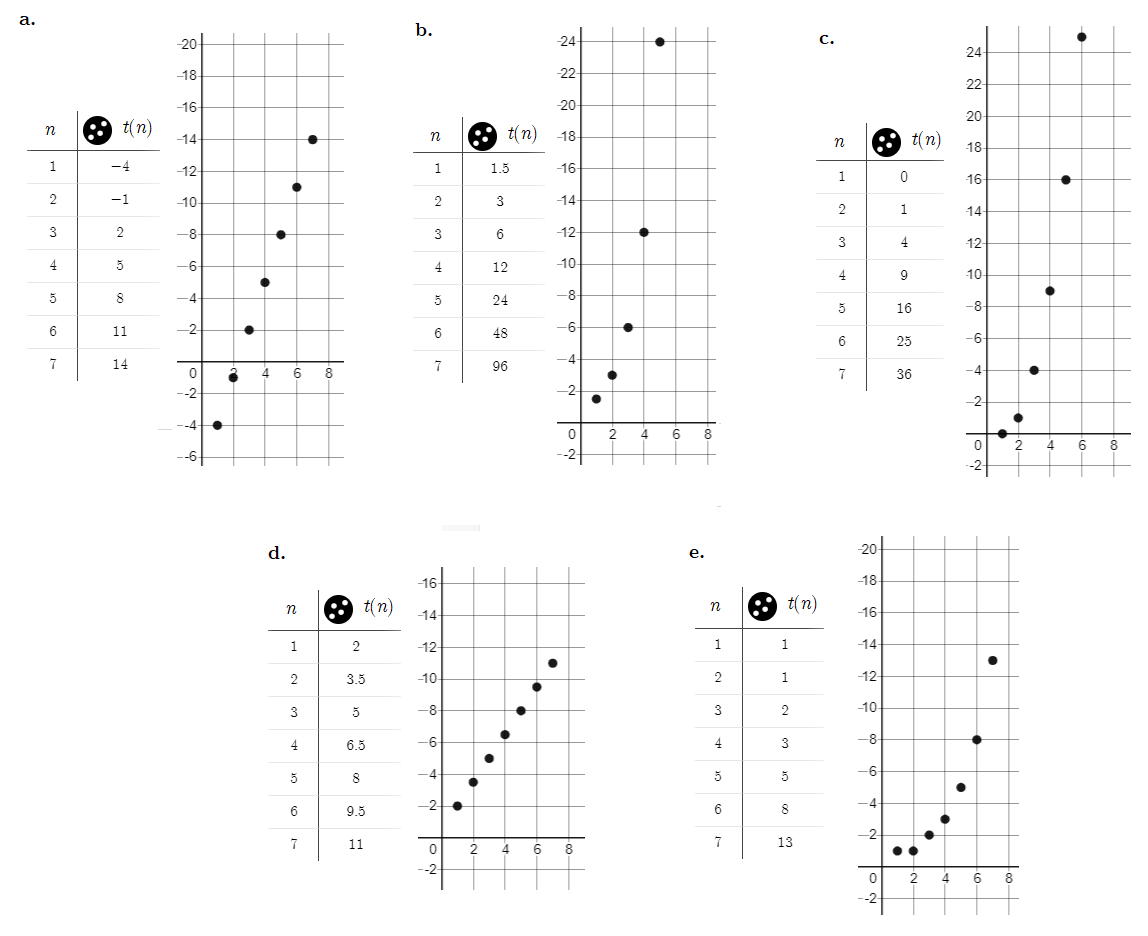
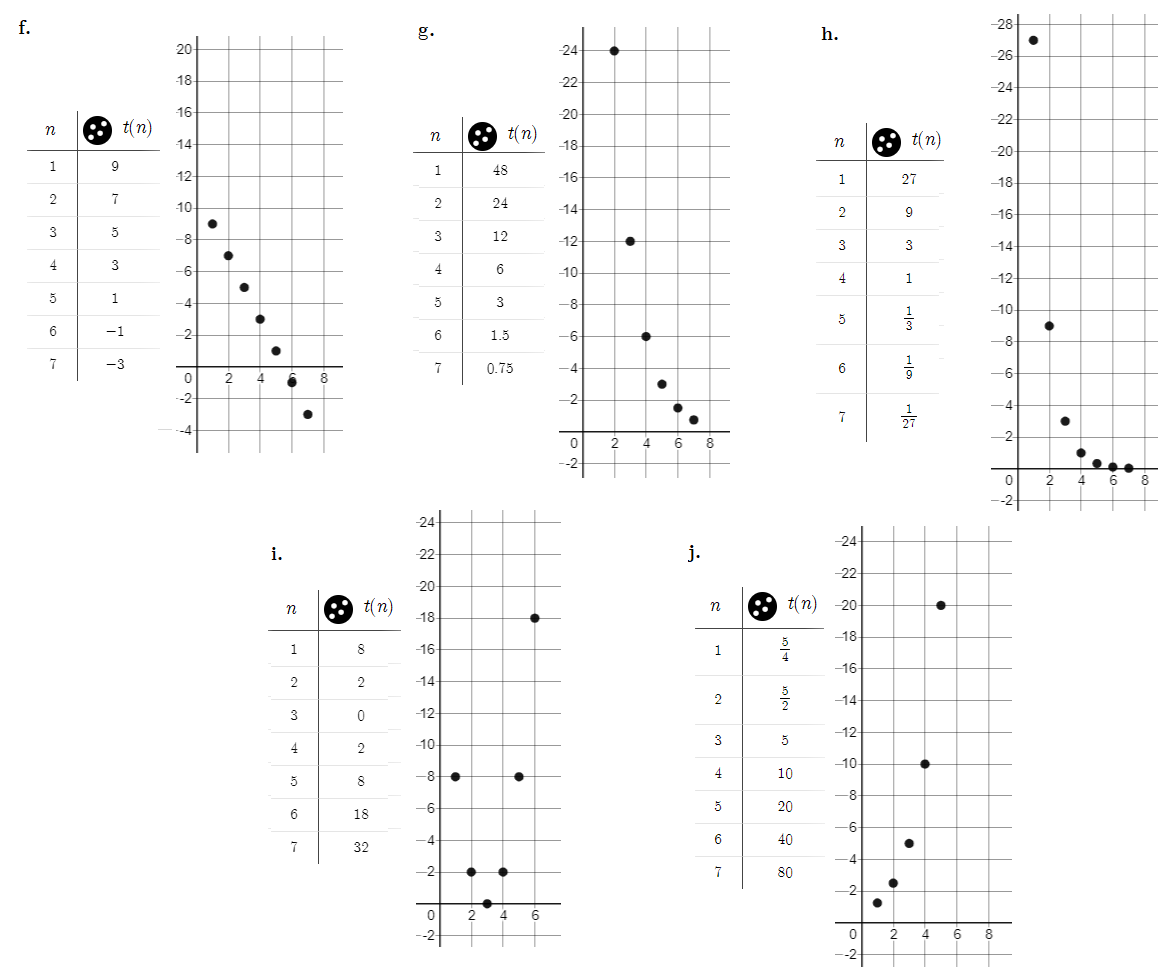
The sequence at $e$: each term is the sum of the previous two terms.
The sequence at $g$: there is each term previous term divided by the $2$.
The sequence at $h$: there is each term previous term divided by $3$.
At sequence $a$, each term is the sum of the previous term and $3$.
At sequence $c$, each term is the sum of the previous term and an odd number.
At sequence $d$, each term is the sum of the previous term and $1.5$.
At sequence $i$ there is not any pattern.
* $bullet$ There is a common difference between consecutive terms.
* $bullet$ When graphed, the points representing the terms lie on the same line.
* $bullet$ The growth is linear so we can compare it to a linear function and thus, a pattern rule can be found using the form: $y=mx+b$ or in this case, $t(n)=mn+t(0)$.
Here we have the following formulas:
$$
S_{n}-a_{1}+…+a_{n}=dfrac{n}{2}(2a_{1}+(n-1)d)
$$
$$
a_{n}=a_{1}+(n-1)d
$$
$$
d=a_{n}-a_{n-1}
$$
$a_{n}=a_{1}+(n-1)d$;
$d=a_{n}-a_{n-1}$
The sequence (f) is $9, 7, 5, 3,cdots$
We can assume that the sequence generator adds $-2$ to the each previous term. Hence it should be included to the family of arithmetic sequence.
$textbf{(b)}$ The sequences which falls into the family of geometric sequence are (b) , (g) , (h) and (j)
The sequence (f) is $27, 9, 3, 1,cdots$
We can assume that the sequence generator multiply $dfrac{1}{3}$ to the each previous term. Hence it should be included to the family of geometric sequence.
The (extended) sequences for (c) and (i) are:
$$
begin{align*}
&text{(c): }0,1,4,9, 16,25,36\
&text{(i): }8,2,0,2,8,18, 32,50,72
end{align*}
$$
As what we have found, the similarity is that these two sequences are in the same family in a sense that squaring is involved in finding the terms: (c) is the perfect squares and (d) is twice the perfect squares.
$textbf{b.}$
The terms of the Fibonacci sequence rely on the previous terms unlike the other three sequences which can be found using their term numbers.
b. The terms of the Fibonacci sequence rely on the previous terms unlike the other three sequences which can be found using their term numbers.
$$
begin{align*}
a_1&=475\
a_2&=290\
a_3&=175\
a_4&=100\
a_5&=60
end{align*}
$$
Lets find out the common difference between the consecutive terms to check for the arithmetic sequence.
$$
begin{align*}
a_2-a_1&=475-290=185\
a_3-a_2&=290-175=115\
a_4-a_3&=175-100=75\
a_5-a_4&=100-60=40
end{align*}
$$
We can see that the common difference between the terms is not a constant number, hence it does belong to family of arithmetic sequence.
Lets find the common ratio of consecutive terms to check for the geometric sequence.
$$
begin{align*}
dfrac{a_1}{a_2}&=dfrac{475}{290}=1.637\
dfrac{a_2}{a_3}&=dfrac{290}{175}=1.657\
dfrac{a_3}{a_4}&=dfrac{175}{100}=1.75\
dfrac{a_4}{a_5}&=dfrac{100}{60}=1.667
end{align*}
$$
We can see that the common ratio is also not the same. hence this sequence also not belongs to the family of geometric sequence.
$textbf{(b)}$ By using the argument of the previous option we can see that the given sequence is neither arithmetic nor geometric and belongs to something else.
$$
begin{align*}
text{no. of pencils required}&=dfrac{3.844times 10^8}{1.8 times 10^{-1}}\
&=dfrac{3.844}{1.8}times dfrac{10^8}{10^{-1}}tag{use $dfrac{a^m}{a^n}=a^{m-n}$}\
&=2.135times 10^{8-(-1)}\
&=2.135times 10^{8+1}\
&boxed{2.135times 10^{9}}
end{align*}
$$
Therefore, we will require approximately $2.136times 10^9$ pencils to cover the distance between earth and moon.
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we have given points as $(-2,1)$ and $(2,-11)$. Let $(x_1,y_1)=(-2,1)$ and $(x_2,y_2)=(2,-11)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{-11-1}{2-(-2)}\
&=dfrac{-12}{2+2}\
&=dfrac{-12}{4}\
&=-3
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $-3$ passing through a point $(-2,1)$ is given by
$$
begin{align*}
y-(1)&=-3cdot (x-(-2))\
y-1&=-3cdot x -3cdot (+2)\
y-1&=-3cdot x-6\
y=-3cdot x-6+1\
&boxed{y=-3 x-5}
end{align*}
$$
y=-3x-5
$$
Now, the chocolate chips required to make 8 dozen muffins
$$
begin{align*} &=text{ounces per dozen} times text{8 dozen}\
&=dfrac{16}{3} times 8\
&=dfrac{16times 8}{3}\
&approx 43 text{ ounces}
end{align*}
$$
If it is a right angled triangle then we can easily find the length of base and height of the triangle and easily calculate the area of the triangle as
$$
text{Area}=dfrac{1}{2}cdot text{Base}times text{perpendicular height}
$$
Now, for calculating the length of the line segment joining 2 vertices we can apply the formula to calculate the distance between the coordinates points on the graph.
The distance between the two points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{distance}=sqrt{(y_2-y_1)^2+(x_2-x_1)^2}
$$
From the figure we can say that the segment AC is making the perpendicular distance of the triangle which is
$$
begin{align*}
text{length}_{AC}&=sqrt{(260-(-10))^2+(525-525)^2}\
&=sqrt{270^2+0^2}\
&=sqrt{270^2}\
&=270
end{align*}
$$
Similarly, The segment AB is making the base of the triangle.
$$
begin{align*}
text{length}_{AB}&=sqrt{(260-260)^2+(725-525)^2}\
&=sqrt{0^2+200^2}\
&=sqrt{200^2}\
&=200
end{align*}
$$
Therefore, the area of the $Delta$ABC is given by
$$
begin{align*}
text{Area}&=dfrac{1}{2}cdottext{Base}times text{perpendicular height}\
&=dfrac{1}{2}cdot 200times 270\
&=dfrac{54000}{2}\
&boxed{27000} text{ unit}^2
end{align*}
$$
Let $w(n)$ represents the amount of liters of water in the tank at the end of $n^text{th}$ day.
$$
begin{align*}
w(0)&=8000\
w(1)&=8000cdot dfrac{1}{2}=4000\
w(2)&=8000cdot dfrac{1}{2}=2000\
w(3)&=8000cdot dfrac{1}{2}=1000\
w(4)&=8000cdot dfrac{1}{2}=500
end{align*}
$$
Therefore, the amount of water in the tank on the $4^text{th}$ day will be 500 liters.
$textbf{(b)}$ Lets calculate the general representation of amount of water in the tank at the end of $n^text{th}$ day
$$
begin{align*}
w(0)&=8000\
w(1)&=8000cdot dfrac{1}{2}=4000=8000cdot(dfrac{1}{2})^1 \
w(2)&=8000cdot dfrac{1}{2}=2000=8000cdot(dfrac{1}{2})^2\
w(3)&=8000cdot dfrac{1}{2}=1000=8000cdot(dfrac{1}{2})^3 \
w(n)&=8000cdot dfrac{1}{2}=8000cdot(dfrac{1}{2})^n \
end{align*}
$$
Hence, we can calculate the amount of water at the end of the $8^text{th}$ day by putting value of $n$ equal to 8 in the equation $w(n)=8000cdot(dfrac{1}{2})^n$
$$
begin{align*}
w(8)&=8000cdot(dfrac{1}{2})^8\
&=8000cdot (dfrac{1}{256})\
&=dfrac{8000}{256}\
&boxed{31.25}
end{align*}
$$
$textbf{(b)}$ The amount of water at the end of the $8^text{th}$ day will be 31.25 liters.
{color{#4257b2}text{a)}}
$$
$$
begin{align*}
y+0.03y& {=}quad :color{#c34632}1.03y\
end{align*}
$$
{color{#4257b2}text{b)}}
$$
$$
begin{align*}
z-0.2z& {=}quad :color{#c34632} 0.8z\
end{align*}
$$
{color{#4257b2}text{c)}}
$$
$$
begin{align*}
x+0.002x& {=}quad : color{#c34632}1.002x\
end{align*}
$$
color{#4257b2} text{ a) }1.03y
$$
$$
color{#4257b2} text{ b) }0.8z
$$
$$
color{#4257b2} text{ c) }1.002x
$$
Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, we have given points as $(2,150)$ and $(4,130)$. Let $(x_1,y_1)=(2,150)$ and $(x_2,y_2)=(3,130)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{130-150}{4-2}\
&=dfrac{-20}{2}\
&=-10
end{align*}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $-10$ passing through a point $(2,150)$ is given by
$$
begin{align*}
y-(150)&=-10cdot (x-2)\
y-150&=-10cdot x -10cdot -2\
y-150&=-10cdot x +20\
y&=-10 cdot x + 20+150\
&boxed{y=-10 x + 170}
end{align*}
$$
y=-10 x + 170
$$
$textbf{(b)}$ $f(0.5b)$ is ” the output for the input that is half of $b$ “.
$textbf{(c)}$ $f(d)+12$ is ” the output which is 12 more than the output for input $d$”
$textbf{(b)}$ $f(0.5b)$ is ” the output for the input that is half of $b$ “.
$textbf{(c)}$ $f(d)+12$ is ” the output which is 12 more than the output for input $d$”
$$
y_1=20-4t
$$
we can represent the given condition of Heinrick’s ponds as shown below
$$
y_2=29-7t
$$
$textbf{(a)}$ We need to find the time when the number of lily pads remaining in each pond will be same. This means we need to equate both $y_1$ and $y_2$ and solve for $t$
$$
begin{align*}
Rightarrow\
20-4t&=29-7ttag{add $7t$ to the each side}\
20-4t+7t&=29-7t+7t\
20+3t&=29tag{subtract 20 from each side}\
20-20+3t&=29-20\
3t&=9tag{divide each side by 3}\
t&=3
end{align*}
$$
Therefore, after 3 hours there will be same number of lily pads in the both the ponds.
$textbf{(b)}$ we can put $t=3$ in any of the equation above to find the number of lily pads after 3 hours when number of the lily pads are the same.
$$
begin{align*}
y_1&=20-4t\
&=20-4(3)\
&=20-12\
&=8
end{align*}
$$
Therefore, there will be 8 lily pads in the each ponds at the time when the number becomes equal.
$textbf{(b)}$ There will be 8 lily pads in the each ponds at the time when the number becomes equal.
An expression which represents the total number of birds is:
$$
G+D+C+E+S+B+L+F
$$
#### (b)
An expression which represents the percentage of birds they saw at the lake is:
$$
dfrac{100text{L}}{G+D+C+E+S+B+L+F}
$$
#### (c)
An expression which represents the fraction of birds that were geese or ducks is:
$dfrac{E}{G+D+C+E+S+B+L+F}$ or $dfrac{D}{G+D+C+E+S+B+L+F}$
textbf{(b)} The first term of the sequence is $-9$ which is represented by $t(1)$.\\
textbf{(c)} The sequence generator is a function which takes each previous term of a sequence as input and provides the next term of sequence as output. For example in case of a arithmetic sequence a sequence generator takes each term as input then add a constant value to it to give the next term of the sequence which will go to the another sequence generator as input which will add a constant value and give the next term of the sequence. This process continued as long as we want to generate the terms of this sequence.\\
textbf{(d)}
begin{center}
begin{tabular}{|p{2cm}|p{2cm}|}
hline
$n$&$t(n)$\
hline
0&-13\
hline
1&-9\
hline
2&-5\
hline
3&-1\
hline
4&3\
hline
5&7\
hline
6&11\
hline
7&15\
hline
end{tabular}
end{center}
textbf{(e)} The graph is attached below. The graph is discrete as the sequence does not take all values of numbers\
$textbf{(g)}$
$$
begin{align*}
t(1)&=-9\
t(2)&=-5=-9+4=t(1)+4times(1)=-9+4times(2-1)\
t(3)&=-1=-5+4=t(2)+4=-9+4+4=-9+4times (3-1)\
&boxed{t(n)=-9+4times (n-1)}
end{align*}
$$
$textbf{(h)}$ As the sequence can start from term number 0 (which gives its zeroth term which is not listed generally) and can have only positive integral value of term number. Therefore, the domain for the sequence is set of whole numbers ($0,1,2,3,4,5,cdots$)
$textbf{(i)}$ $t(n)$ represents the zeroth term of the sequence when $n=0$ which can be found out by putting $n=0$ into general form equation
$$
t(0)=-9+4times(0-4)=-9-4=-13
$$
$textbf{(b)}$ $-9$
$textbf{(c)}$ The sequence generator is a function which takes each previous term of a sequence as input and provides the next term of sequence as output.
$textbf{(d)}$ Table is attached inside.
$textbf{(e)}$ See the graph inside.
$textbf{(f)}$ The common difference is $4$ which is the difference of the $y$ coordinates of the consecutive points on the graph. This does make sense because difference of the $y$ coordinates of any two consecutive points represents the common difference which should be constant and same for every difference of consecutive terms.
$textbf{(g)}$ $t(n)=-9+4times (n-1)$
$textbf{(h)}$ As the sequence can start from term number 0 (which gives its zeroth term) and will have only positive integral value of term number. Therefore, the domain for the sequence is set of whole numbers ($0,1,2,3,4,5,cdots$)
$textbf{(i)}$ $t(n)$ represents the zeroth term of the sequence when $n=0$ which is $-13$ in this case.
$textbf{(a)}$ The first term of this sequence is $-4$.
For the common difference we can find difference between any two consecutive terms in order of higher term number subtracted from lower term number. This gives common difference as $-1-(-4)=3$
Now. zeroth term can be found by subtracting common difference from the first term as it is a previous term than the first. which implies
$$
t(0)=-4-(3)=-7
$$
$textbf{(b)}$ The general term of an arithmetic sequence is given by
$$
t(n)=t(1)+(n-1)cdot d
$$
where $t(1)$ is the first term of the sequence and $d$ is the common difference and $n$ represents the term number. For this sequence , we have $t(1)=-4$ and $d=3$ so equation for $t(n)$ can be found out by putting these value in the general form which gives
$$
t(n)=-4+(n-1)cdot 3
$$
Now, we can check if the given terms of the sequence satisfy it or not.
$bullet$ Checking for $t(2)=-1$
$$
begin{align*}
t(n)&=-4+(n-1)cdot 3\
t(2)&=-4+(2-1)cdot 3\
-1&=-4+1cdot 3\
-1&=-1tag{true}
end{align*}
$$
$bullet$ Checking for $t(3)=2$
$$
begin{align*}
t(3)&=-4+(3-1)cdot 3\
2&=-4+2cdot 3\
2&=-4+6\
2&=2 tag{true}
end{align*}
$$
$bullet$ Checking for $t(4)=5$
$$
begin{align*}
t(4)&=-4+(4-1)cdot 3\
5&=-4+3cdot 3\
5&=-4+9\
5&=5 tag{true}
end{align*}
$$
$$
begin{align*}
t(n)&=-4+(n-1)cdot 3\
42&=-4+ncdot 3-1cdot 3\
42&=-4-3+3n\
42&=-7+3ntag{add 7 to the each side}\
42+7&=-7+7+3n\
49&=3ntag{divide each side by 3}\
n&=dfrac{49}{3}
end{align*}
$$
The value of $n$ obtained is not integral and hence 42 cannot be a term of of the sequence.
$textbf{(d)}$ Yes, given function $f(x)=3x-7$ can obtain a value 42 because it can take all real values for input $x$. Unlike the sequence equation it is not constrained to only take integral values of inputs. Hence it will take the value 42 corresponding to $x=dfrac{49}{3}$
$textbf{(e)}$ The $t(n)$ is a discrete function which can take only whole number as input and have only discrete outputs. whereas $f(x)$ is a continuous function which can take any real value of $x$ as input and have all real values as output.
$textbf{(b)}$ $t(n)=-4+(n-1)d$
$textbf{(c)}$ No
$textbf{(d)}$ yes
$textbf{(e)}$ The $t(n)$ is a discrete function which can take only whole number as input and have only discrete outputs. whereas $f(x)$ is a continuous function which can take any real value of $x$ as input and have all real values as output.
$$
y=mx+b
$$
or in this case,
$$
t(n)=mn+t(0)
$$
Representing the two terms as points, we have $(5,11)$ and $(50,371)$ so the slope is:
$$
m=dfrac{Delta y}{Delta x }=dfrac{371-11}{50-5}=dfrac{360}{45}=8
$$
This is also the sequence generator.
To find $t(0)$, use the slope and either of the two points. I used $(5,11)$:
$$
begin{align*}
11&=8(5)+t(0)\
11&=40+t(0)\
-29&=t(0)\
color{#c34632}t(0)&= color{#c34632}-29
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=8n-29
$$
$t(0)=-29$
$$
t(n)=8n-29
$$
$$
t(5)=11
$$
$$
t(50)=371
$$
We know that the general term of an arithmetic progression is given by
$$
t(n)=a+(n-1)d
$$
where, $t(n)$ represents the $n^text{th}$ term of the sequence , $a$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
We can put the given known value ot terms into the equations and solve for the values of $a$ and $d$ as shown below.
$$
begin{align*}
t(n)&=a+(n-1)d\
t(5)&=a+(5-1)d\
11&=a+4d
end{align*}
$$
$$
begin{align*}
t(n)&=a+(n-1)d\
t(50)&=a+(50-1)d\
471&=a+49d
end{align*}
$$
So, we have 2 unknown and 2 equation in two variables, which are
$$
begin{align}
11&=a+4d\
371&=a+49d
end{align}
$$
$$
begin{align*}
371-11&=(a-a)+(49-4)d\
360&=45dtag{divide each side by 45}\
dfrac{360}{45}&=dfrac{45d}{45}\
8&=d
end{align*}
$$
Now, we can put $d=8$ in any of the equation to solve for $a$.
$$
begin{align*}
11&=a+4d\
11&=a+4(8)\
11&=a+32tag{subtract 32 from each side}\
11-32&=a+32-32\
-21&=a
end{align*}
$$
Now, we can put $a=-21$ and $d=8$ to write the final equation.
$$
begin{align*}
boxed{t(n)=-21+(n-1)8}
end{align*}
$$
As $a$ in the sequence represent first term which means $a=t(1)$. To find $t(0)$ we can subtract common difference $d$ from the first term $t(1)$.
$$
begin{align*}
t(0)&=t(1)-d\
t(0)&=(-21)-(8)\
&boxed{t(0)=-29}
end{align*}
$$
t(n)=-21+(n-1)8
$$
$$
t(0)=-29
$$
We know that the general term of an arithmetic progression is given by
$$
t(n)=a+(n-1)d
$$
where, $t(n)$ represents the $n^text{th}$ term of the sequence , $a$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
Given that $t(3)=52$ and $t(7)=108$
We can put the given known value ot terms into the equations and solve for the values of $a$ and $d$ as shown below.
$$
begin{align*}
t(n)&=a+(n-1)d\
t(3)&=a+(3-1)d\
52&=a+2d
end{align*}
$$
$$
begin{align*}
t(n)&=a+(n-1)d\
t(7)&=a+(7-1)d\
108&=a+6d
end{align*}
$$
So, we have 2 unknown and 2 equation in two variables, which are
$$
begin{align}
52&=a+2d\
108&=a+6d
end{align}
$$
To solve the above equation, first subtract eq(1) from the eq(2), which will result in
$$
begin{align*}
108-52&=(a-a)+(6-2)d\
56&=4dtag{divide each side by 4}\
dfrac{56}{4}&=dfrac{4d}{4}\
14&=d
end{align*}
$$
begin{align*}
52&=a+2d\
52&=a+2(14)\
52&=a+28tag{subtract 28 from each side}\
52-28&=a+28-28\
24&=a
end{align*}
Now, we can put $a=24$ and $d=14$ to write the final equation.
begin{align*}
boxed{t(n)=24+(n-1)14}
end{align*}
So we can fin the terms of the sequence by putting value of $n$ in the general equation. The table of values is attached below.\
begin{center}
begin{tabular}{|p{1.5cm}|p{2cm}|}
hline
term no. & term value\
hline
1&24\
hline
2&38\
hline
3&52\
hline
4&66\
hline
5&70\
hline
end{tabular}
end{center}
$$
begin{align*}
t(n)&=24+(n-1)14\
t(17)&=24+(17-1)14\
t(17)&=24+16cdot 14\
t(17)&=24+224\
t(17)&=248
end{align*}
$$
Therefore, there will be 248 cards in his collection after 10 years from now.
$textbf{(c)}$ We have already determined the equation in the part (a).
$$
boxed{t(n)=24+(n-1)14}
$$
where, $t(n)$ represents the $n^text{th}$ term of the sequence , $24$ represents the first term of the sequence, $14$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
$textbf{(b)}$ $248$ cards
$textbf{(c)}$ $t(n)=24+(n-1)14$
$$
y=mx+b
$$
or in this case,
$$
t(n)=mn+t(0)
$$
We are given that $m=-17$ and representing the term as a point, we have $(16,93)$, we can find $t(0):$
$$
begin{align*}
93&=-17(16)+t(0)\
93&=-272+t(0)\
365&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=-17n+365
$$
t(n)=-17n+365
$$
$$
t(n)=a+(n-1)d
$$
where, $t(n)$ represents the $n^text{th}$ term of the sequence , $a$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
We are given $t(15)=735$ and common difference $d=20$
So, we can put the given known value ot terms into the equations and solve for the value of
$a$ which in our case represent the price at the beginning of the day.
$$
begin{align*}
t(n)&=a+(n-1)d\
t(15)&=a+(15-1)d\
735&=a+14(20)\
735&=a+280tag{subtract 280 from each side}\
735-280&=a+280-280\
455&=a
end{align*}
$$
Therefore, the price at the beginning of the day was $455.\\
textbf{(b)} \Now, it is given that the contest always starts with $100 which means$t(1)=100$and we need to find the value of term number$n$corresponding to$t(n)=1360$
$$
begin{align*}
t(n)&=a+(n-1)d\
1360&=100+(n-1)20\
1360&=100+(n)20-20\
1360&=80+20ntag{subtract 80 from each side}\
1360-80&=80-80+20n\
1280&=20ntag{divide each side by 20}\
dfrac{1280}{20}&=dfrac{20n}{20}\
64&=n
end{align*}
$$
Therefore, we can say that 64th person was the winner and hence, 63 people must have answered the questions incorrectly.
$textbf{(b)}$ 63 people answered the questions incorrectly.
$$
begin{align*}
t(9)&=t(8)+22=164+22=186\
t(10)&=t(9)+22=186+22=208\
t(11)&=t(10)+22=208+22=230\
t(12)&=t(11)+22=230+22=252\
t(13)&=t(12)+22=252+22=274ne 300
end{align*}
$$
Since we did not obtain $t(13)=300$ using the slope, then it is not possible to create an arithmetic sequence to fit her information.
From the given information regarding terms, we can find out the the $d$ value of the resultant arithmetic sequence. If that matches with the slope then the given situation is possible else not.
Given that $t(8)=164$ and $t(13)=300$
Now, general term of an arithmetic series is given by
$$
t(n)=t(1)+(n-1)d\
$$
From the given conditions, we can generate equations as shown below
$$
begin{align}
164&=t(1)+(8-1)d\
300&=t(1)+(13-1)d
end{align}
$$
On subtracting the equation (1) from equation (2), we get
$$
begin{align*}
36&=5d\
d&=dfrac{36}{5}\
d&=27.2
end{align*}
$$
We got $d$ value which is not equal to the given slope and hence creating such arithmetic sequence is not possible for given conditions.
$$
y=mx+b
$$
or in this case,
$$
t(n)=mn+t(0)
$$
$textbf{a.}$
Find the slope (or sequence generator) using two points, say $(3,10)$ and $(7,54)$:
$$
m=dfrac{Delta y}{Delta x }=dfrac{54-10}{7-3}=dfrac{44}{4}=11
$$
Using any point, say $(3,10)$, solve for $t(0)$:
$$
begin{align*}
10&=11(3)+t(0)\
10&=33+t(0)\
-23&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=11n-23
$$
$textbf{b.}$
Find the slope (or sequence generator) using two points, $(100,10)$ and $(70,100)$:
$$
m=dfrac{Delta y}{Delta x }=dfrac{100-10}{70-100}=dfrac{90}{-30}=-3
$$
Using any point, say $(100,10)$, solve for $t(0)$:
$$
begin{align*}
10&=-3(100)+t(0)\
10&=-300+t(0)\
310&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=-3n+310
$$
b. $t(n)=-3n+310$
$$
t(n)=a+(n-1)d
$$
where, $t(n)$ represents the $n^text{th}$ term of the sequence , $a$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
We can put any two given known value ot terms into the equations and solve for the values of $a$ and $d$ as shown below. Lets put $t(7)=54$ and $t(3)=10$ for making the equations.
$$
begin{align*}
t(n)&=a+(n-1)d\
t(7)&=a+(7-1)d\
54&=a+6d
end{align*}
$$
$$
begin{align*}
t(n)&=a+(n-1)d\
t(3)&=a+(3-1)d\
10&=a+2d
end{align*}
$$
So, we have 2 unknown and 2 equation in two variables, which are
$$
begin{align}
54&=a+6d\
10&=a+2d
end{align}
$$
To solve the above equation, subtract eq(2) from the eq(1), which will result in
$$
begin{align*}
54-10&=(a-a)+(6-2)d\
44&=4dtag{divide each side by 4}\
dfrac{44}{4}&=dfrac{4d}{4}\
11&=d
end{align*}
$$
$$
begin{align*}
10&=a+2d\
10&=a+2(11)\
10&=a+22tag{subtract 22 from each side}\
10-22&=a+22-22\
-12&=a
end{align*}
$$
Now, we can put $a=-12$ and $d=11$ to write the final equation.
$$
begin{align*}
boxed{t(n)=-12+(n-1)11}
end{align*}
$$
We can test our general form equation by verifying it for $t(19)=186$ and $t(16)=153$.
Lets test it for $t(19)=186$ first.
$$
begin{align*}
t(n)&=-12+(n-1)11\
186&=-12+(19-1)11\
186&=-12+(18)11\
186&=-12+198\
186&=186
end{align*}
$$
hence, our general equation is valid for $t(19)=186$ and Similarly, we can also test for $t(16)=153$.
$$
Rightarrow
$$
$$
begin{align*}
t(n)&=a+(n-1)d\
t(100)&=a+(100-1)d\
10&=a+99d
end{align*}
$$
$$
begin{align*}
t(70)&=a+(70-1)d\
100&=a+(69)d
end{align*}
$$
So, we have 2 unknown and 2 equation in two variables, which are
$$
begin{align}
10&=a+99d\
100&=a+(69)d
end{align}
$$
To solve the above equation, subtract eq(2) from the eq(1), which will result in
$$
begin{align*}
10-100&=(a-a)+(99-69)d\
-90&=30dtag{divide each side by 30}\
dfrac{-90}{30}&=dfrac{30d}{30}\
-3&=d
end{align*}
$$
Now, we can put $d=-3$ in the equation (2) to solve for $a$.
$$
begin{align*}
100&=a+(69)d\
100&=a+69(-3)\
100&=a-207tag{add 207 to the each side}\
100+207&=a-207+207\
307&=a
end{align*}
$$
Now, we can put $a=307$ and $d=-3$ to write the final equation.
$$
begin{align*}
t(n)=307+(n-1)(-3)\
boxed{t(n)=307-3(n-1)}
end{align*}
$$
$textbf{(b)}$ $t(n)=307-3(n-1)$
Personally, I do not agree because although you can find an equation for an arithmetic sequence the same way as finding an equation for a linear function, their graphs are different. The graph of an arithmetic sequence is discrete while it is continuous for linear functions. This also means that for the same equation, the domains and range of the two are different.
$textbf{a.}$
Solve for $t(n)=447$:
$$
begin{align*}
5n-3&=447\
5n&=450\
n&=90
end{align*}
$$
Since $90$ is a positive integer, then 447 is a term of this sequence and it is the $text{textcolor{#c34632}{90th term}}$.
$textbf{b.}$
Solve for $t(n)=447$:
$$
begin{align*}
24-5n&=447\
-5n&=423\
n&=-84.6
end{align*}
$$
Since $-84.6$ is not a positive integer, then 447 is not a term of this sequence.
Solve for $t(n)=447$:
$$
begin{align*}
-6+3(n-1)&=447\
3(n-1)&=453\
n-1&=151\
n&=152
end{align*}
$$
Since $152$ is a positive integer, then 447 is a term of this sequence and it is the $text{textcolor{#c34632}{152nd term}}$.
$textbf{d.}$
Solve for $t(n)=447$:
$$
begin{align*}
14-3n&=447\
-3n&=433\
n&=-dfrac{433}{3}
end{align*}
$$
Since $-dfrac{433}{3}$ is not a positive integer, then 447 is not a term of this sequence.
$textbf{e.}$
Solve for $t(n)=447$:
$$
begin{align*}
-8-7(n-1)&=447\
-7(n-1)&=455\
n-1&=-65\
n&=-64
end{align*}
$$
Since $-64$ is not a positive integer, then 447 is not a term of this sequence.
b. No
c. Yes ; 152nd term
d. No
e. No
{color{#4257b2}text{ a) }}
$$
$$
begin{align*}
&text{Switch sides}\
&5n-3=447\\
&5n-3+3=447+3 tag{Add 3 to both sides} \
&5n=450 tag{Simplify} \
&frac{5n}{5}=frac{450}{5} tag{Divide both sides by 5} \\
&boxed{{color{#c34632} n=90 } }
end{align*}
$$
{color{#4257b2}text{ b) }}
$$
$$
begin{align*}
&text{Switch sides}\
&24-5n=447\\
&24-5n-24=447-24 tag{Subtract 24 from both sides} \
&-5n=423 tag{Simplify} \
&frac{-5n}{-5}=frac{423}{-5} tag{Divide both sides by -5} \\
&boxed{{color{#c34632} n= -frac{423}{5} } }
end{align*}
$$
{color{#4257b2}text{ c) }}
$$
$$
begin{align*}
&text{Switch sides}\
&-6+3left(n-1right)=447\\
&-6+3left(n-1right)+6=447+6 tag{Add 6 to both sides} \
&3left(n-1right)=453 tag{Simplify} \
&frac{3left(n-1right)}{3}=frac{453}{3} tag{Divide both sides by -5} \
& n-1=151 tag{Simplify} \
&n-1+1=151+1 tag{Add 1 to both sides}\\
&boxed{{color{#c34632} n= 152 } }
end{align*}
$$
{color{#4257b2}text{ d) }}
$$
$$
begin{align*}
&text{Switch sides}\
&14-3n=447\\
&14-3n-14=447-14 tag{Subtract 14 from both sides} \
&-3n=433 tag{Simplify} \
&frac{-3n}{-3}=frac{433}{-3} tag{Divide both sides by -3} \\
&boxed{{color{#c34632} n= -frac{433}{3} } }
end{align*}
$$
{color{#4257b2}text{ e) }}
$$
$$
begin{align*}
&text{Switch sides}\
&-8-7left(n-1right)=447\\
&-8-7left(n-1right)+8=447+8 tag{Add 8 to both sides} \
&-7left(n-1right)=455 tag{Simplify} \
&frac{-7left(n-1right)}{-7}=frac{455}{-7} tag{Divide both sides by -7} \
&n-1=-65 tag{Simplify} \
&n-1+1=-65+1 tag{Add 1 to both sides}\\
&boxed{{color{#c34632} n= -64 } }
end{align*}
$$
color{#4257b2} text{a)}n=90
$$
$$
color{#4257b2} text{b)} n= -frac{423}{5}
$$
$$
color{#4257b2} text{c)}152
$$
$$
color{#4257b2} text{d)} n= -frac{433}{3}
$$
$$
color{#4257b2} text{e)}n=-64
$$
$$
begin{align*}
t(n)&=14-3n\
447&=14-3n tag{subtract 14 from each side}\
447-14&=14-14 -3n\
433&=-3ntag{divide each side by -3}\
dfrac{433}{-3}&=dfrac{-3n}{-3}\
n&=dfrac{433}{-3}
end{align*}
$$
Now, As n represents the term number so it cannot take negative values and fractional value. In fact $n$ should be a whole number $(0, 1, 2, 3, 4,cdots)$
For the sequence $t(n)=14-3n$ we got the fractional term number corresponding to the term 447. hence it cannot be a term of the sequence.
For the sequence $t(n)=14-3n$ we got the fractional term number corresponding to the term 447. hence it cannot be a term of the sequence.
$$
y=mx+b
$$
or in this case,
$$
t(n)=mn+t(0)
$$
$textbf{a.}$
The slope (or sequence generator) is the difference of two conseuctive terms:
$$
m=7-4=10-7=13-10=3
$$
Since $t(1)=4$ and the sequence generator is $3$, then:
$$
begin{align*}
t(1)&=t(0)+3\
4&=t(0)+3\
1&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=3n+1
$$
$textbf{b.}$
The slope (or sequence generator) is the difference of two conseuctive terms:
$$
m=8-3=13-8=5
$$
Since $t(1)=3$ and the sequence generator is $5$, then:
$$
begin{align*}
t(1)&=t(0)+5\
3&=t(0)+5\
-2&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=5n-2
$$
The slope (or sequence generator) is the difference of two conseuctive terms:
$$
m=19-24=14-19=-5
$$
Since $t(1)=24$ and the sequence generator is $-5$, then:
$$
begin{align*}
t(1)&=t(0)-5\
24&=t(0)-5\
29&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=-5n+29
$$
$textbf{d.}$
The slope (or sequence generator) is the difference of two conseuctive terms:
$$
m=9.5-7=12-9.5=2.5
$$
Since $t(1)=7$ and the sequence generator is $2.5$, then:
$$
begin{align*}
t(1)&=t(0)+ 2.5\
7&=t(0)+ 2.5\
4.5&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=2.5n+4.5
$$
b. $t(n)=5n-2$
c. $t(n)=-5n+29$
d. $t(n)=2.5n+4.5$
$textbf{(a)}$ Taking difference of first two term can also give the value of $d$.
$$
Rightarrow d=7-4=3
$$
Now, general term of arithmetic sequence is given by $t(n)=t(1)+(n-1)d$
$$
begin{align*}
Rightarrow t(n)&=3+(n-1)cdot 3\
t(n)&=4+3n-3\
t(n)&=3n+1
end{align*}
$$
$textbf{(b)}$
$$
d=8-3=5
$$
Now, general term of arithmetic sequence is given by $t(n)=t(1)+(n-1)d$
$$
begin{align*}
Rightarrow t(n)&=3+(n-1)cdot 5\
t(n)&=3+5n-5\
t(n)&=5n-2
end{align*}
$$
$textbf{(c)}$
$$
d=19-24=-5
$$
Now, general term of arithmetic sequence is given by $t(n)=t(1)+(n-1)d$
$$
begin{align*}
Rightarrow t(n)&=24+(n-1)cdot -5\
t(n)&=24-5n+5\
t(n)&=29 -5n
end{align*}
$$
$textbf{(d)}$
$$
d=9.5-7=1.5
$$
Now, general term of arithmetic sequence is given by $t(n)=t(1)+(n-1)d$
$$
begin{align*}
Rightarrow t(n)&=7+(n-1)cdot 1.5\
t(n)&=7+1.5n-1.5\
t(n)&=1.5n +5.5
end{align*}
$$
$textbf{(b)}$ $d=5$ and $t{n}=5n-2$
$textbf{(c)}$ $d=-5$ and $t{n}=29-5n$
$textbf{(d)}$ $d=1.5$ and $t{n}=1.5n+5.5$
$$
t(n)=t(n-1)+dfrac{t(n-1)}{10}
$$
Every year the ticket price is increasing 10 percent of the price in the previous year.
The general ticket price in nth year in the terms of price into the starting year is given by
$$
t(n)=50cdot (dfrac{110}{100})^{n}
$$
$textbf{(b)}$ The price of the admission in the 6th year can be found out by putting 6 at the place of $n$ into the general ticket price shown in previous part.
$$
begin{align*}
t(n)&=50cdot (dfrac{110}{100})^{n}\
t(6)&=50cdot (dfrac{110}{100})^{6}\
t(6)&=50cdot (1.771)\
t(6)&=88.578approx $88.58
end{align*}
$$
$textbf{(b)}$ $$88.58$
$textbf{(b)}$ The given residual plot tells that the predictions made for taller swimmers are more accurate than the prediction made for shorter swimmers. This can be explained by the magnitudes of the residuals. The far the point is from the best fit line, the more will be the magnitude of residual and hence more will be the error in the prediction.
$textbf{(b)}$ The given residual plot tells that the predictions made for taller swimmers are more accurate than the prediction made for shorter swimmers. This can be explained by the magnitudes of the residuals. The far the point is from the best fit line, the more will be the magnitude of residual and hence more will be the error in the prediction.
$$
mathrm{hypotenuse}^2= mathrm{base}^2 + mathrm{height}^2
$$
In the given figure, we have
hypotenuse=137 feet
and base=105 feet
Now, applying pythagoras theorem
$$
137^2=105^2 + mathrm{height}^2
$$
This implies,
$$
mathrm{height}=sqrt{137^2 -105^2}
$$
$$
=88 >feet
$$
$textbf{(a)}$
Now, for calculating the $10^text{th}$ term one way is that we keep adding common difference to the previously known terms until we reach $10^text{th}$ term. From teh sequence we have $t(4)=10$ now, we can proceed in the way explained above.
$$
begin{align*}
t(5)&=10+6=16\
t(6)&=16+6=22\
t(7)&=22+6=28\
t(8)&=28+6=34\
t(9)&=34+6=40\
t(10)&=40+6=46
end{align*}
$$
We have got $t(10)=46$ but this method is not efficient and will not be helpful for finding the term of the sequence with very high term number. To avoid this, we can find the the explicit equation to represent any term $t(n)$, which is our method 2 and explained below.
$bullet$ The general term of an arithmetic progression is given by
$$
t(n)=a+(n-1)d
$$
where, $t(n)$ represents the $n^text{th}$ term of the sequence , $a$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
We have $a=-8$ and $d=6$, so we can put these value to obtain the explicit equation.
$$
begin{align*}
t(n)&=(-8)+(n-1)(6)\
&boxed{t(n)=-8+(n-1)6}
end{align*}
$$
Now, we can find the $t(10)$ by putting $n=10$ into the explicit equation.
$$
begin{align*}
t(10)&=-8+(10-1)6\
t(10)&=-8+54\
t(10)&=46
end{align*}
$$
$textbf{(c)}$ The recursive equation is when we try to write any next term by using previous terms. As for an arithmetic sequence each next term can be obtained by adding $d$ to its previous term. Therefore, we can represent this in form of recursive equation as shown below.
$$
begin{align*}
t(n+1)&=t(n)+6 tag{put $t(n)=-8+(n-1)6$}\
t(n+1)&=-8+(n-1)6+6\
t(n+1)&=-8+6n-6+6\
&boxed{t(n+1)=-8+6n}
end{align*}
$$
$textbf{(b)}$ $t(n+1)=t(n)+6=-8+6n$
$textbf{(b)}$He got the different sequence because he started with 0 where in the correct sequence(previous problem) the first term is -8. For writing the correct sequence Alejandro should know the value of starting term. If he has access to $t(1)$ from the correct sequence then he can write the exact sequence by using recursive equation.
In other words, we can say that recursive equation is not unique unless we fixed a term of it.
$textbf{(b)}$He got the different sequence because he started with 0 where in the correct sequence(previous problem) the first term is -8. For writing the correct sequence Alejandro should know the value of starting term. If he has access to $t(1)$ from the correct sequence then he can write the exact sequence by using recursive equation.
$$
begin{align*}
t(1) &= 3\
t(2)&=t(1)^2-1=3^2-1=9-1=8\
t(3)&=t(2)^2-1=8^2-1=64-1=63\
t(4)&=t(3)^2-1=63^2-1=3969-1=3968
end{align*}
$$
$textbf{(b)}$ Avery’s sequence is neither Arithmetic nor Geometric. It is some other king of the sequence as we cannot represent the terms of these sequence by general term equations of Arithmetic sequence which is given by $t(n)=t(0)+(n-1)d$ nor by Geometric sequences whose general term is given by $t(n)=acdot r^{n-1}$.
$textbf{(c)}$ Collin could determine the $10^{th}$ term by the method shown above. For this one needs to find the $9^{th}$ term first which needs $8^{th}$ and so on. At some point one will needing only first term which is already given in question.
$textbf{(b)}$ Avery’s sequence is neither Arithmetic nor Geometric.
$textbf{(c)}$ For this Collin needs to find the $9^{th}$ term first, which needs $8^{th}$ and so on. At some point he will be needing only first term which is already given in question.
Since you are subtracting $2$ from (or adding $-2$ to) the previous term, then the sequence is arithmetic. To find an explicit equation, use the formula:
$$
t(n)=mn+t(0)
$$
which is similar to the slope-intercept form of a line, $y=mx+b$.
The sequence generator is $m=-2$. Given that $t(2)=19$, we can use this to find $t(0)$:
$$
begin{align*}
19&=-2(2)+t(0)\
19&=-4+t(0)\
23&=t(0)
end{align*}
$$
So, the explicit equation is:
$$
color{#c34632}t(n)=-2n+23
$$
$textbf{b.}$
From the equation, we know that the sequence generator is $m=8$. We must state a known term, say $t(1)=6(1)+8=14$ to write a recursive rule so a possible answer is:
$$
color{#c34632}t(1)=14,t(n+1)=t(n)+8
$$
b. $t(1)=14,t(n+1)=t(n)+8$
From the recursive equation we can see that a term of a Fibonacci sequence can be determined by sum of its previous two terms. So, we can find out the $t(3)$ as shown below.
begin{align*}
t(3)&=t(2)+t(1)\
t(3)&=1+1\
t(3)&=2
end{align*}
Now, we can find out the $t(4)$ as shown below.
begin{align*}
t(4)&=t(3)+t(2)\
t(4)&=2+1\
t(4)&=3
end{align*}
Similarly, we can find the each and every term by proceeding in the same manner. The table of value are attached below.\
begin{center}
begin{tabular}{|p{2cm}|p{2cm}|}
hline
n&t(n)\
hline
1&1\
hline
2&1\
hline
3&2\
hline
4&3\
hline
5&5\
hline
6&8\
hline
7&13\
hline
8&21\
hline
9&34\
hline
10&55\
hline
end{tabular}
end{center}
$textbf{(c)}$ In order to calculate the value of $100^text{th}$ term of Fibonacci sequence we need values of $99^text{th}$ and $98^text{th}$ terms of Fibonacci sequence. Now, for the value of $99^text{th}$ term we need values of $98^text{th}$ and $97^text{th}$ terms of Fibonacci sequence. Which goes on like this until we reach the known value of a term of Fibonacci series.
In other way, we need to go from bottom to top, we have to start from term 1 and then find term 2 using recursive equation.we keep doing it until we reach $100^text{th}$ term.
$textbf{(b)}$ Fibonacci sequence is neither arithmetic nor geometric sequence.
$textbf{(c)}$ In order to calculate the value of $100^text{th}$ term of Fibonacci sequence we need values of $99^text{th}$ and $98^text{th}$ terms of Fibonacci sequence. Now, for the value of $99^text{th}$ term we need values of $98^text{th}$ and $97^text{th}$ terms of Fibonacci sequence. Which goes on like this until we reach the known value of a term of Fibonacci series.
$$
begin{align*}
t(0)&=4.5(0)-8=-8\
t(1)&=4.5(1)-8=-3.5\
t(2)&=4.5(2)-8=1\
t(3)&=4.5(3)-8=5.5
end{align*}
$$
Therefore, first 4 terms for the given explicit equation are $(-8, -3.5, 1, 5.5)$
$textbf{(b)}$ To find the $15^text{th}$ term of the sequence we need to put $n$ equal to 14 in the explicit equation. This is because we have started from the $t(0)$ as the first term.
$$
begin{align*}
t(14)&=4.5(14)-8=55
end{align*}
$$
$textbf{(c)}$ For writing the explicit equation we need to write the general term the sequence with the help of its previous term. which can be proceeded in the way shown below.
lets assume that there is linear relationship between $t(n+1)$ and $t(n)$, so we can write it as
$$
t(n+1)=acdot t(n)+c
$$
Now we can put the known values of term in this equation to make two equations in two variables so that we can able to solve for the $a$ and $c$
We have $t(0)=-8$ and $t(1)=-3.5$
$$
begin{align*}
t(0+1)&=acdot t(0)+c tag{by putting $n=0$}\
t(1)&=acdot t(0)+c tag{put known values}\
-3.5&=acdot -8+c\
-3.5&=-8a+c
end{align*}
$$
We have $t(1)=-3.5$ and $t(2)=1$
$$
begin{align*}
t(1+1)&=acdot t(1)+c tag{by putting $n=1$}\
t(2)&=acdot t(1)+c tag{put known values}\
1&=acdot -3.5+c\
1&=-3.5a+c
end{align*}
$$
$$
begin{align}
-3.5&=-8a+c\
1&=-3.5a+c
end{align}
$$
Subtract the eq(1) from the eq(2)
$$
begin{align*}
1-(-3.5)&=(-3.5-(-8))a+c-c\
1+3.5&=(-3.5+8)a\
4.5&=4.5atag{divide each side by 4.5}\
a&=1
end{align*}
$$
Use the value $a=1$ into the eq(2) and solve for $c$
$$
begin{align*}
1&=-3.5(1)+c\
1&=-3.5+ctag{add 3.5 to the each side}\
1+3.5&=-3.5+3.5+c\
4.5&=c
end{align*}
$$
Now, put $a=1$ and $c=4.5$, so the final recursive equation becomes
$$
begin{align*}
t(n+1)&=acdot t(n)+c\
t(n+1)&=1cdot t(n)+4.5\
t(n+1)&=t(n)+4.5
end{align*}
$$
$bullet$ The more convenient way to write the recursive equation is by observing that each next term can be obtained by adding 4.5 into the previous term. therefore, we can simply write the recursive equation as
$$
t(n)=t(n-1)+4.5
$$
which is also equivalent to
$$
boxed{t(n+1)=t(n)+4.5}
$$
$textbf{(b)}$ To find the $15^text{th}$ term of the sequence we need to put $n$ equal to 14 in the explicit equation. This is because we have started from the $t(0)$ as the first term.
$textbf{(c)}$ $t(n+1)=t(n)+4.5$
$$
y=mx+b
$$
or in this case,
$$
t(n)=mn+t(0)
$$
The slope (or sequence generator) is the difference of two conseuctive terms:
$$
m=8-5=11-8=14-11=17-14=3
$$
Since $t(1)=5$ and the sequence generator is $3$, then:
$$
begin{align*}
t(1)&=t(0)+3\
5&=t(0)+3\
2&=t(0)
end{align*}
$$
So, the explicit equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=3n+2
$$
From the explicit equation, we know that the sequence generator is $m=3$. We must state a known term, say $t(1)=3(1)+2=5$ to write a recursive rule so a possible answer is:
$$
color{#c34632}t(1)=5,t(n+1)=t(n)+3
$$
recursive: $t(1)=5,t(n+1)=t(n)+3$
$$
begin{align*}
t(1)&=5\
t(2)&=8=5+3=5+(2-1)cdot 3\
t(3)&=11=5+3+3=5+(3-1)cdot 3\
t(4)&=14=5+3+3+3=5+(4-1)cdot 3\
t(n)&=5+(n-1)cdot 3
end{align*}
$$
Therefore, the explicit equation for the sequence is
$$
boxed{t(n)=5+(n-1)cdot 3}
$$
Now, for recursive equation we can represent each next term by using previous term as shown below.
$$
begin{align*}
t(1)&=5\
t(2)&=8=5+3=t(1)+3\
t(3)&=11=8+3=t(2)+3\
t(4)&=14=11+3=t(3)+3\
t(n+1)&=t(n)+3
end{align*}
$$
Therefore, the recursive term for the sequence is
$$
boxed{t(n+1)=t(n)+3}
$$
$$
t(n)=5+(n-1)cdot 3
$$
$textbf{(b)}$ The recursive term for the sequence is
$$
t(n+1)=t(n)+3
$$
Use the Distributive Property: $a(b+c)=ab+ac$
$$
(4x+5)(4x-5)= (4x+5)4x-(4x+5)5
$$
Use the Distributive Property again:
$$
= 16x^2+20x-20x-25
$$
Simplify:
$$
= color{#c34632}16x^2-25
$$
$textbf{b.}$
The expression also means:
$$
(4x+5)^2= (4x+5)(4x+5)
$$
Use the Distributive Property: $a(b+c)=ab+ac$
$$
= (4x+5)4x+(4x+5)5
$$
Use the Distributive Property again:
$$
= 16x^2+20x+20x+25
$$
Simplify:
$$
= color{#c34632}16x^2+40x+25color{white}tag{1}
$$
b. $16x^2+40x+25$
{color{#4257b2}text{a)}}
$$
$$
begin{align*}
left(4x+5right)left(4x-5right)& {=}quad : left(4xright)^2-5^2\
&left(4xright)^2=4^2x^2=16x^2 tag{Simplify} \
&5^2=25 tag{Simplify} \
&={color{#c34632}16x^2-25}
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad left(a+bright)left(a-bright)=a^2-b^2
$$
$$
color{#c34632} text{ }a=4x,:b=5
$$
$$
text{ }
$$
{color{#4257b2}text{b)}}
$$
$$
begin{align*}
left(4x+5right)^2& {=}quad : left(4xright)^2+2cdot :4xcdot :5+5^2\
&=16x^2+40x+5^2 \
&={color{#c34632}16x^2+40x+25}
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Apply:distributing:rule}:quad left(a+bright)^2=a^2+2ab+b^2
$$
$$
color{#c34632} text{ }a=4x,::b=5
$$
$$
text{ }
$$
color{#4257b2} text{ a) }16x^2-25
$$
$$
color{#4257b2} text{ b) }16x^2+40x+25
$$
$$
text{ }
$$
begin{tabular}{ |p{2cm}|p{2cm}|p{2cm}| }
hline
Month & Stamps \
hline
0 & 120 \1 & 132 \2 & 144 \3& 156\4&168\5&180\6&192
\7&204\8&216\9&228\10&240\
11&252\12&264\
hline
end{tabular}
It can be seen from the table above, Lona will have 264 stamps in a year.
c.
$t(mathrm{n})=120+12mathrm{n}$,
where n is the number of months
d.
$$
begin{align*}
500&=120+12mathrm{n} \
380&=12mathrm{n} tag{text{subtracting 120 from each side}}\
Rightarrow mathrm{n}&=dfrac{380}{12}\
end{align*}
$$
Now, $dfrac{380}{12}$ months implies 31 months and 20 days.
b. 264 stamps
c. $t(mathrm{n})=120+12mathrm{n}$
d. No, If we are talking about exactly 12 tickets for each month then on 32th month she will have 4 extra tickets. Her book will be filled completely in 31 months and 20 days.
In the given situation the $r$ value is $-0.45$, which shows there is somewhat negative relationship in dietary fibre and the blood cholesterol, which is not perfectly linear. Hence, Scientist’s finding shows that increase in dietary fibre results in decrease in blood cholesterol. Similarly, Decrease in Dietary fibre in the meals signifies more blood cholesterol.
$$
begin{align*}
y_{sc}&=1500cdot m+10000
end{align*}
$$
Now, also given that It has also sold 18,000 graphing calculators and continues to sell 1300 of this model each month . let $y_{gc}$ represents the number of scientific calculators sold then this situation can be represented in the form of equation as shown below.
$$
begin{align*}
y_{gc}&=1300cdot m+18000
end{align*}
$$
$textbf{(a)}$ Given that the number of scientific calculators sold is equal to the number of graphing calculators sold.
$$
Rightarrow
$$
$$
begin{align*}
y_{sc}&=y_{gc}\
1500cdot m+10000&=1300cdot m+18000
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
1500cdot m+10000&=1300cdot m+18000 tag{subtract 10000 from each side}\
1500cdot m+10000-10000&=1300cdot m+18000-10000\
1500cdot m&=1300cdot m+8000tag{subtract $1300cdot m$ from each side}\
1500cdot m-1300cdot m&=1300cdot m-1300cdot m+8000\
200m&=8000tag{divide each side by 200}\
dfrac{200m}{200}&=dfrac{8000}{200}\
m&=40
end{align*}
$$
Therefore, after 40 months the sale of both types of calculators will become equal.
$textbf{(b)}$ After 40 months the sale of both types of calculators will become equal.
$$
begin{align*}&text{For less than 3 years – Sequence A}\
&text{For more than 3 years – Sequence B}
end{align*}
$$
$textbf{(b)}$ Sequence B will be more suitable if amount is to be kept for many years.
begin{tabular}{|p{1cm}|p{1cm}|}
hline
multicolumn{2}{|c|}{Sequence A} \
hline
$n$ & $t(n)$\
hline
5&135\
hline
6&162\
hline
7&189\
hline
end{tabular}\\\
begin{tabular}{|p{1cm}|p{1cm}|}
hline
multicolumn{2}{|c|}{Sequence C} \
hline
$n$ & $t(n)$\
hline
5&96\
hline
6&192\
hline
7&384\
hline
end{tabular}
\\\
textbf{(d)} Due to extension the answer will not change. Because, after 3 years the Sequence gives the highest amount of returns than any other sequence.
$textbf{(b)}$ Sequence B will be more suitable if amount is to be kept for many years.
$textbf{(c)}$ See the tables Inside.
$textbf{(d)}$ Due to extension the answer will not change. Because, after 3 years the Sequence gives the highest amount of returns than any other sequence.
Here, the conclusion is that an exponentially growing bank account will contain more money than a linearly growing bank account.
#### (b)
Here is the growth of a given sequence equivalent to a linearly growing, so, the conclusion is that the bigger growth is exponential growth.
$$
begin{align*}
t(1)&=12\
t(2)&=144=12times 12=12cdot t(1)\
t(3)&=1728=12times 144=12cdot t(2)
end{align*}
$$
$Rightarrow$ The above sequence is Geometric with common ratio $=12$ and the growth is exponential for this sequence.
$textbf{(b)}$ $0,5,10,15,20,25,cdots$
$$
begin{align*}
t(1)&=0\
t(2)&=5=0+5=t(1)+5\
t(3)&=10=5+5=t(2)+5\
t(4)&=15=10+5=t(3)+5\
t(5)&=20=15+5=t(4)+5
end{align*}
$$
$Rightarrow$ The above sequence is Arithmetic with common difference $=5$ and the growth is linear for this sequence.
For the above given sequence we cannot find neither common ratio nor common difference hence the given sequence is neither Geometric nor Arithmetic.
$textbf{(d)}$ $1.5, 2.25, 3.375, 5.0625,cdots$
$$
begin{align*}
t(1)&=1.5\
t(2)&=2.25=1.5times 1.5=1.5cdot t(1)\
t(3)&=3.375=1.5times 2.25=1.5cdot t(2)\
t(4)&=5.0625=1.5times 3.375=1.5cdot t(3)
end{align*}
$$
$Rightarrow$ The above sequence is Geometric with common ratio $=1.5$ and the growth is exponential for this sequence.
$textbf{(b)}$ Arithmetic sequence; Linear growth
$textbf{(c)}$ Neither
$textbf{(d)}$ Geometric sequence; Exponential growth
$$
begin{align*}
t(1)&=-3\
t(2)&=-2cdot t(1)=-2cdot -3=6\
t(3)&=-2cdot t(2)=-2cdot 6=-12\
t(4)&=-2cdot t(3)=-2cdot -12=24\
t(5)&=-2cdot t(4)=-2cdot 24=-48
end{align*}
$$
Therefore, the first five terms for the sequence are $(-3, 6, -12, 24, -48)$
$textbf{(b)}$ The given recursive equation is $t(n+1)=t(n)-5$ . We can find the first five terms of sequence by putting value of $n$ starting from 1 to 5.
$$
begin{align*}
t(1)&=8\
t(2)&=t(1)-5=8-5=3\
t(3)&=t(2)-5=3-5=-2\
t(4)&=t(3)-5=-2-5=-7\
t(5)&=t(4)-5=-7-5=-12
end{align*}
$$
Therefore, the first five terms for the sequence are $(8, 3, -2, -7, -12)$
$$
t(n+1)=dfrac{1}{t(n)}
$$
Now, we can find the first five terms of sequence by putting value of $n$ starting from 1 to 5.
$$
begin{align*}
t(1)&=2\
t(2)&=dfrac{1}{t(1)}=dfrac{1}{2}\
t(3)&=dfrac{1}{t(2)}=dfrac{1}{dfrac{1}{2}}=2\
t(4)&=dfrac{1}{t(3)}=dfrac{1}{2}\
t(5)&=dfrac{1}{t(4)}=dfrac{1}{dfrac{1}{2}}=2
end{align*}
$$
Therefore, the first five terms for the sequence are $(2, dfrac{1}{2}, 2, dfrac{1}{2}, 2)$
$textbf{(b)}$ $(8, 3, -2, -7, -12)$
$textbf{(c)}$ $(2, dfrac{1}{2}, 2, dfrac{1}{2}, 2)$
$$
begin{align*}
4x-5&=2x+9tag{add 5 to the each side}\
4x-5+5&=2x+9+5\
4x&=2x+14tag{subtract $2x$ from each side}\
4x-2x&=2x-2x+14\
2x&=14tag{divide each side by 2}\
dfrac{2x}{2}&=dfrac{14}{2}\
x&=7
end{align*}
$$
As $x$ is a part of angle therefore, it should be mentioned as 7$text{textdegree}$.
x=7text{textdegree}
$$
$$
A=dfrac{1}{2}(b_1+b_2)h
$$
where, $b_1$ and $b_2$ are the lengths of the bases(parallel sides) and $h$ is perpendicular height.
Now, given that the area of the trapezoid is 56 $text{cm}^2$ and also $b_1=10$ cm and $b_2=6$ cm. By putting these known values into the equation of area we can solve for $h$.
$$
begin{align*}
A&=dfrac{1}{2}(b_1+b_2)h\
56&=dfrac{1}{2}(10+6)h\
56&=dfrac{16}{2}h\
56&=8htag{divide each side by 8}\
dfrac{56}{8}&=dfrac{8h}{8}\
7&=h\
&boxed{h=7 text{ cm}}
end{align*}
$$
h=7 text{ cm}
$$
{color{#4257b2}text{a)}}
$$
$$
begin{align*}
left(2m^3right)left(4m^2right)& {=}quad : 2m^3cdot :4m^2tag{Remove parentheses}\
&=8m^3m^2 tag{Multiply the numbers} \
&=8m^{3+2} \
&={color{#c34632}8m^5}
end{align*}
$$
$$
color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad :a^bcdot :a^c=a^{b+c}
$$
$$
text{ }
$$
{color{#4257b2}text{b)}}
$$
$$
begin{align*}
frac{6y^5}{3y^2}& {=}quad : frac{2y^5}{y^2}tag{Divide the numbers}\
&=2y^{5-2} \
&={color{#c34632}2y^3}
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad frac{x^a}{x^b}:=:x^{a-b}
$$
$$
text{ }
$$
{color{#4257b2}text{c)}}
$$
$$
begin{align*}
frac{-4y^2}{6y^7}& {=}quad : -frac{4y^2}{6y^7}\
&=-frac{2y^2}{3y^7} tag{Cancel the common factor 2}\
&frac{y^2}{y^7}=frac{1}{y^{7-2}}=frac{1}{y^5}tag{Simplify}\
&={color{#c34632}-frac{2}{3y^5}}
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b}
$$
$$
color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad frac{x^a}{x^b}:=:frac{1}{x^{b-a}}
$$
{color{#4257b2}text{d)}}
$$
$$
begin{align*}
left(-2x^2right)^3& {=}quad : -left(2x^2right)^3\
&=-2^3left(x^2right)^3 \
&=-2^3x^{2cdot :3}\
&={color{#c34632}-8x^6}
end{align*}
$$
$$
color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad left(-aright)^n=-a^n,:mathrm{if:}nmathrm{:is:odd}
$$
$$
color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad left(acdot :bright)^n=a^nb^n
$$
$$
color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad left(a^bright)^c=a^{bc}
$$
$$
text{ }
$$
color{#4257b2}text{ a) } 8m^5
$$
$$
color{#4257b2} text{ b) } 2y^3
$$
$$
color{#4257b2} text{ c) } -frac{2}{3y^5}
$$
$$
color{#4257b2} text{ d) }-8x^6
$$
$$
y-y_1=mcdot (x-x_1)
$$
Now, given that the line has slope $=2$ and passing through (10, 17) hence the equation of line can be written as shown below.
$$
begin{align*}
y-17&=2cdot(x-10)\
y&=2x-3
end{align*}
$$
$textbf{(b)}$ Slope of a line passing through two given points $(x_1,y_1)$ and $(x_2,y_2)$ is given by
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
Now, given that line passes through (1, -4) and (-2 , 5)
$Rightarrow$
$$
text{slope}=dfrac{5-(-4)}{-2-1}=-3
$$
Therefore, the line with the slope -3 and passing through $(1,-4)$ is
$$
begin{align*}
y-(-4)&=-3cdot(x-1)\
y+4&=-3x+3\
y&=-3x-1
end{align*}
$$
Let the two points are $(3,0)$ and $(6,2)$.
$Rightarrow$
$$
text{slope}=dfrac{2-0}{6-3}=dfrac{2}{3}
$$
Now, the equation of the line with slope $=dfrac{2}{3}$ and passing through $(3,0)$ is
$$
begin{align*}
y-(0)&=dfrac{2}{3}cdot(x-3)\
y&=dfrac{2}{3}x-2\
end{align*}
$$
$textbf{(d)}$ From the graph we can see that the line passes through points $(0,9)$ and $4,19$, hence this also can be solved similar to that of part $textbf{(b)}$.
Slope of line passing through points $(0,9)$ and $4,19$
$$
text{slope}=dfrac{19-9}{4-0}=dfrac{5}{2}
$$
Now, the equation of the line with slope $=dfrac{5}{2}$ and passing through $(0,9)$ is
$$
begin{align*}
y-(9)&=dfrac{5}{2}cdot(x-0)\
y&=dfrac{5}{2}x+9\
end{align*}
$$
$textbf{(b)}$ $y=-3x-1$
$textbf{(c)}$ $y=dfrac{2}{3}x-2$
$textbf{(d)}$ $y=dfrac{5}{2}x+9$
The number of $pi$Phone sold in the first week are given by
$$
=100+100times dfrac{15}{100}=100times 1.15 =115
$$
The number of $pi$Phone sold in the Second week are
$$
=115+115times dfrac{15}{100}=115times(1.15)=100times 1.15^2 =132
$$
Here, the multiplier is 1.15 Therefore, number of $pi$Phone sold in $n^{text{th}}$ week can be represented as
$$
text{no. in } n^{text{th } } text{ week}=100times (1.15)^{n}
$$
$$
Rightarrow
$$
Number of $pi$Phone sold during $4^{text{th}}$ week $=100times (1.15)^4=174.9$
which can be approximated to 175 units.
Number of $pi$Phone sold during $10^{text{th}}$ week $=100times (1.15)^{10}=404.5$
which can be approximated to 405 units.
$textbf{(b)}$ It will make a Geometric sequence as its general term can be represented as the general term of a Geometric sequence which is given by $t(0)times (r)^{n-1}$
$textbf{(c)}$ If the number of $pi$Phones sold during week 51 is known, then the number of $pi$Phones sold in the week 52 can be found out by multiplying the week $51^{text{th}}$ data by 1.15
The recursive equation can be written as $t(n+1)=t(n)times (1.15)$
$$
begin{align*}
t(0)&=100\
t(1)&=100+100times dfrac{15}{100}=100times (1.15)=115\
t(2)&=115+115times dfrac{15}{100}=115times (1.15)=100times (1.15)^2\
t(3)&=100times (1.15)^2+(100times (1.15)^2)times dfrac{15}{100}=100times (1.15)^2(1+0.15)=100times (1.15)^3\
& boxed{ t(n)=100times (1.15)^n}
end{align*}
$$
Yes, result matches with the part $textbf{(a)}$.
$textbf{(e)}$
$$
begin{align*}
t(52)&=100times (1.15)^52\
&=100times (1433.1369)\
&=143313.7
end{align*}
$$
Therefore, the number of $pi$Phones sold during week 52 are approximately 143314 units.
$textbf{(b)}$ Geometric Sequence
$textbf{(c)}$ By multiplying with 1.15
$textbf{(d)}$ $t(n)=100times (1.15)^n$, Yes
$textbf{(e)}$ 143314 units
Since the graph of a geometric sequence is an exponential graph when the terms are connected, then we can use the exponential equation:
$$
y=acdot b^x
$$
or in this case,
$$
t(n)= t(0)cdot b^n
$$
Let $n$ be the number of weeks so that $t(n)$ is the number of orders. The sequence generator is the multiplier $b$. Since the sales increase by 7% each week, then:
$$
b=100%+7%=107%=1.07
$$
Since $t(0)=10000$ and the sequence generator is $1.07$, the the explicit equation is:
$$
color{#c34632}t(n)=10000(1.07)^n
$$
From the explicit equation, we know that the sequence generator is $1.07$. We must state a known term, say $t(0)=10000$ (which is given) to write a recursive rule so a possible answer is:
$$
color{#c34632}t(0)=10000,t(n+1)= 1.07cdot t(n)
$$
Change the multiplier from 1.07 to 1.17 to find the new equations. The explicit equation will be:
$$
color{#c34632}t(n)=10000(1.17)^n
$$
and the recursive rule is:
$$
color{#c34632}t(0)=10000,t(n+1)= 1.17cdot t(n)
$$
b. explicit: $t(n)=10000(1.17)^n$ ; recursive: $t(0)=10000,t(n+1)= 1.17cdot t(n)$
$textbf{(a)}$
$$
begin{align*}
text{week(0) } t(0)&=10000\
text{week(1) } t(1)&=10000-dfrac{3}{100}cdot 10000=10000-300=9700\
text{week(2) } t(2)&=9700-dfrac{3}{100}cdot 9700=9700-291=9409\
text{week(3) } t(3)&=9409-dfrac{3}{100}cdot 9409=9409-282.27=9126.73\
text{week(4) } t(4)&=9126.73-dfrac{3}{100}cdot 9126.73=9126.73-273.80=8852.92
end{align*}
$$
Finding the sales after $10^text{th}$ week ($t(10)$) by above procedure will take longer, but if someone has to find the $t(10)$ by this method only, the idea is clear. Instead we can find explicit and recursive equation first. Then we can calculate the $t(10)$ very easily.
$textbf{(b)}bullet$ Finding the explicit equation
$$
begin{align*}
t(0)&=10000\
t(1)&=10000-dfrac{3}{100}cdot 10000=10000(dfrac{100-3}{100})=10000(0.97)\
t(2)&=10000 (0.97)-dfrac{3}{100}cdot 10000(0.97)=10000(0.97)(dfrac{100-3}{100})=10000(0.97)^2\
t(3)&=10000 (0.97)^2-dfrac{3}{100}cdot 10000(0.97)^2=10000(0.97)^2(dfrac{100-3}{100})=10000(0.97)^3\
&boxed{t(n)=10000(0.97)^n}
end{align*}
$$
$$
begin{align*}
t(0)&=10000\
t(1)&=10000(0.97)=t(0)(0.97)\
t(2)&=10000(0.97)(0.97)=t(1)(0.97)\
&boxed{t(n+1)=t(n)(0.97)}
end{align*}
$$
$textbf{(c)}$ We can verify our $4^text{th}$ week sale by calculating it with explicit equation.
$$
begin{align*}
t(n)&=10000(0.97)^n\
t(4)&=10000(0.97)^4\
t(4)&=10000(0.88529281)\
t(4)&=8852.92
end{align*}
$$
We can see that the result matches with the previous calculation. Hence we can say that our explicit equation is correct. similarly we can find the sale of the $10^text{th}$ week that is $t(10)$.
$$
begin{align*}
t(n)&=10000(0.97)^n\
t(10)&=10000(0.97)^10\
t(10)&=10000(0.7374241)\
t(10)&=7374.24
end{align*}
$$
$textbf{(b)}$ $t(n)=10000(0.97)^n$ and $t(n+1)=t(n)(0.97)$
$textbf{(c)}$ Yes, the result from the part a matches after solving it via explicit equation. hence we can say that the explicit equation is valid.
part (a) $rightarrow$ 1.07
part (b) $rightarrow$ 1.17
The multiplier for the problem 5-94 $rightarrow$ 0.97
$textbf{(b)}$ The given sequence is $(8, 8, 8, 8,cdots)$
The multiplier can be determined by taking the ratio of any two consecutive terms with higher term number in numerator and lower term number in denominator.
$Rightarrow$
$$
text{multiplier}=dfrac{8}{8}=1
$$
$textbf{(c)}$ $bullet$ When the multiplier is less than 1 but greater than zero, the sequence will have each of its terms smaller than its previous term. This will result in decreasing or decaying sequence.
$bullet$ When the multiplier is greater than 1, the sequence will have each of its terms greater than its previous term. This will result in increasing or growing sequence.
part (a) $rightarrow$ 1.07
part (b) $rightarrow$ 1.17
The multiplier for the problem 5-94 $rightarrow$ 0.97
$textbf{(b)}$ $text{multiplier}=dfrac{8}{8}=1$
$textbf{(c)}$When the multiplier is less than 1 but greater than zero, the sequence will have each of its terms smaller than its previous term. This will result in decreasing or decaying sequence.
When the multiplier is greater than 1, the sequence will have each of its terms greater than its previous term. This will result in increasing or growing sequence.
The multiplier for 5-92(b) is $frac{11700}{10000}=1.17$
The multiplier for 5-93 is $frac{9700}{10000}=0.97$
If the multiplier is greater than 1, then the sequence is growing sequence. It means that a term is always greater than its preceding term.
In order to find how many weeks it will take for the weekly sales of one Talk per week, we will solve the following equation for $n$ and get the following:
$$
1=10000(0.97)^{n}
$$
$$
(0.97)^n=0.0001
$$
$$
napprox302
$$
So, it will take $302$ weeks.
#### (b)
On the following picture, there is a graph for the sales of $pi$Phones for the first year.
From the previous picture, we can notice that there is no $x$-intercept, but there is an $y$-intercept in the point $(0,100)$.
#### (d)
Here, we actually need to find intercept of those graphs.
So, the conclusion is that it will take about $64$ weeks to exceed the sales in the second equation.
#### (e)
On the following picture, there are graphed both functions in part d) and their intersection.
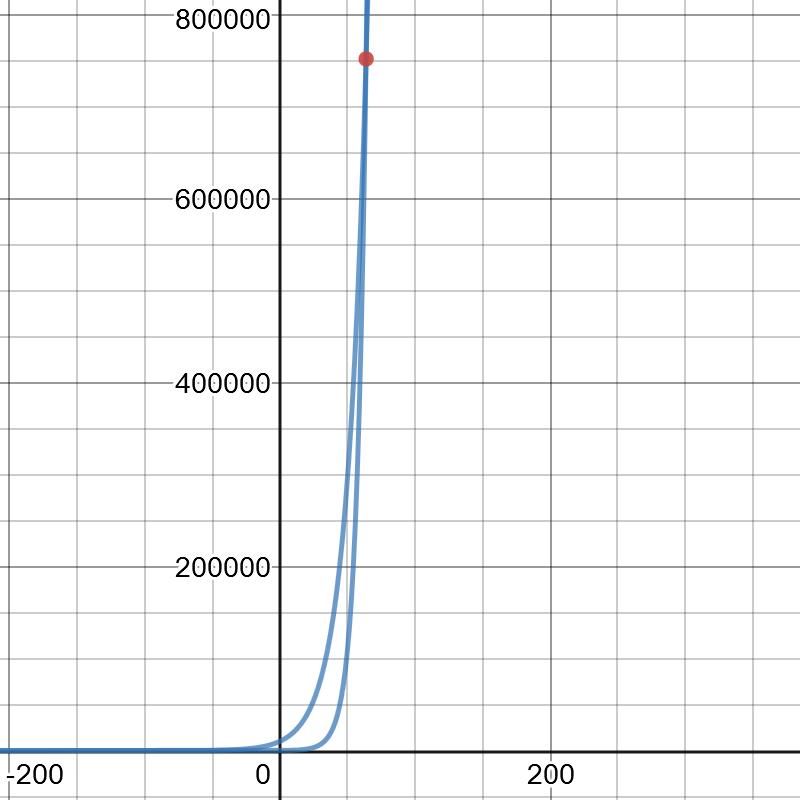
Using the calculator, we get that the answer is $302.3828$, so, our answer from the part a) is very close to this which we got using the calculator.
$$
text{multiplier}=dfrac{2000}{1600}=1.25
$$
Now, we can write its explicit equation as
$$
t(n)=t(0)cdot (1.25)^n=1600(1.25)^n
$$
Checking validity of the equation by finding the values of each term using the equation and then verifying it with table.
$$
begin{align*}
t(n)&=1600(1.25)^n\
t(0)&=1600(1.25)^0tag{first term}\
t(0)&=1600(1)\
t(0)&=1600\
t(1)&=1600(1.25)^1tag{second term}\
t(1)&=1600(1.25)\
t(1)&=2000\
t(2)&=1600(1.25)^2tag{third term}\
t(2)&=1600(1.5625)\
t(2)&=2500\
t(3)&=1600(1.25)^3tag{fourth term}\
t(3)&=1600(1.9531)\
t(3)&=3125\
t(4)&=1600(1.25)^4tag{fifth term}\
t(4)&=1600(2.4414)\
t(4)&=3906
end{align*}
$$
We can see that , each and every term matches with the given table, hence our equation $boxed{t(n)=1600(1.25)^n}$ is valid.
Now, we can write the recursive equation as
$$
boxed{t(n+1)=t(n)cdot (1.25)}
$$
$$
text{multiplier}=dfrac{3125}{3906.25}=0.8
$$
Now, we can write its explicit equation as
$$
t(n)=t(0)cdot (0.8)^n=3906.25(0.8)^n
$$
Checking validity of the equation by finding the values of each term using the equation and then verifying it with table.
$$
begin{align*}
t(n)&=3906.25(0.8)^n\
t(0)&=3906.25(0.8)^0tag{first term}\
t(0)&=3906.25(1)\
t(0)&=3906.25\
t(1)&=3906.25(0.8)^1tag{second term}\
t(1)&=3906.25(0.8)\
t(1)&=3125\
t(2)&=3906.25(0.8)^2tag{third term}\
t(2)&=3906.25(0.64)\
t(2)&=2500\
t(3)&=3906.25(0.8)^3tag{fourth term}\
t(3)&=3906.25(0.512)\
t(3)&=2000\
t(4)&=3906.25(0.8)^4tag{fifth term}\
t(4)&=3906.25(0.4096)\
t(4)&=1600
end{align*}
$$
We can see that , each and every term matches with the given table, hence our equation $boxed{t(n)=3906.25(0.8)^n}$ is valid.
Now, we can write the recursive equation as
$$
boxed{t(n+1)=t(n)cdot (0.8)}
$$
$$
text{multiplier}=dfrac{72}{50}=1.44
$$
Now, we can write its explicit equation as
$$
t(n)=t(0)cdot (1.44)^n=50(1.44)^n
$$
Checking validity of the equation by finding the values of each term using the equation and then verifying it with table.
$$
begin{align*}
t(n)&=50(1.44)^n\
t(0)&=50(1.44)^0tag{first term}\
t(0)&=50(1)\
t(0)&=50\
t(1)&=50(1.44)^1tag{second term}\
t(1)&=50(1.44)\
t(1)&=72\
t(2)&=50(1.44)^2tag{third term}\
t(2)&=50(2.0736)\
t(2)&=103.68\
t(3)&=50(1.44)^3tag{fourth term}\
t(3)&=50(2.985984)\
t(3)&=149.2992\
end{align*}
$$
We can see that , each and every term matches with the given table, hence our equation $boxed{t(n)=50(1.44)^n}$ is valid.
Now, we can write the recursive equation as
$$
boxed{t(n+1)=t(n)cdot (1.44)}
$$
$$
t(n)=t(0)(c)^n
$$
Now, we need to find out the values of $t(0)$ and $c$ by putting the values of known terms into this assumed equation.
$$
begin{align*}
t(n)&=t(0)(c)^n\
t(1)&=t(0)(c)^1tag{putting $t(1)=50$}\
50&=t(0)(c)\
t(3)&=t(0)(c)^3tag{putting $t(3)=72$}\
72&=t(0)(c)^3\
end{align*}
$$
Now, we have 2 equations as shown below
$$
begin{align}
50&=t(0)(c)\
72&=t(0)(c)^3
end{align}
$$
Divide the eq(2) by eq(1), which will result in
$$
begin{align*}
dfrac{72}{50}&=dfrac{t(0)}{t(0)}cdot dfrac{c^3}{c}\
1.44&=c^2tag{take $sqrt{}$ on the both side}\
sqrt{1.44}&=sqrt{c^2}\
1.2&=c
end{align*}
$$
putting $c=1.2$ in eq (1) , we can solve for $t(0)$ as shown below.
$$
begin{align*}
50&=t(0)(1.2)tag{divide each side by 1.2}\
dfrac{50}{1.2}&=dfrac{t(0)(1.2)}{1.2}\
41.66&=t(0)
end{align*}
$$
Now, putting $t(0)=41.66$ and $c=1.2$ in the unknown explicit equation, we can write our final explicit equation as
$$
boxed{t(n)=41.66(1.2)^n}
$$
$$
begin{align*}
t(n)&=41.66(1.2)^n\
t(5)&=41.66(1.2)^5 tag{testing for t(5)}\
103.68&=41.66(2.48832)\
103.68&=103.68 tag{true always}\
t(5)&=41.66(1.2)^5 tag{testing for t(7)}\
149.2992&=41.66(3.5831808)\
149.2992&=149.2992 tag{true always}
end{align*}
$$
We can see that , our equation is valid hence we can use it to write the missing values in the table.
$$
begin{align*}
t(n)&=41.66(1.2)^n\
t(2)&=41.66(1.2)^2\
t(2)&=59.9904\
t(4)&=41.66(1.2)^4\
t(4)&=86.3861\
t(6)&=41.66(1.2)^6\
t(6)&=124.39609
end{align*}
$$
$textbf{(e)}$ The tables in part (a) is reversed order of the table in the part (d) and vice versa.
The multipliers in parts (a) and (b) are multiplicative inverse of each other. This makes sense because one table is written in increasing manner and other is written in decreasing manner. but the values are the same from the ends.
$textbf{(f)}$ we assumed the explicit equation first, then used the value given in the table to solve for the unknowns in the assumed equation.
The odd terms of the table in part (d) are the terms of the table in part (c).
$textbf{(g)}$ From the explicit equation, which we proved valid for part (d), we calculated the $t(2)$ was equal to 59.9904. which is calculated in solution of the part (d).
$textbf{(b)}$ $t(n)=3906.25(0.8)^n$
$textbf{(c)}$ $t(n)=50(1.44)^n$
$textbf{(d)}$ $t(n)=41.66(1.2)^n$
$textbf{(e)}$ The tables in part (a) is reversed order of the table in the part (d) and vice versa.
The multipliers in parts (a) and (b) are multiplicative inverse of each other. This makes sense because one table is written in increasing manner and other is written in decreasing manner. but the values are the same from the ends.
$textbf{(f)}$ we assumed the explicit equation first, then used the value given in the table to solve for the unknowns in the assumed equation.
The odd terms of the table in part (d) are the terms of the table in part (c).
$textbf{(g)}$ From the explicit equation, which we proved valid for part (d), we calculated the $t(2)$ was equal to 59.9904. which is calculated in solution of the part (d).
This is because the tax and discount here can be represented in mathematical terms as a fixed numbers getting multiplied to original cost. Which is for case 1 its multiplication by 1.05 followed by 0.8 and for second case its multiplication by 0.8 followed by 1.05 and due to associative property of multiplication it remains same.
There are 70 squares remained in case 1 after the first discount.
$textbf{(d)}$ There are 56 squares remained in case 1 after the second discount.
There are 56 squares remained in case 2 after the second discount.
$textbf{(e)}$ This result makes sense as the final result here, can be obtained by mathematical multiplication of terms one after another.
For case 1 its multiplication by 0.2 followed by 0.3
For case 2 its multiplication by 0.3 followed by 0.2
Due to associative property of multiplication the result remained same.
case 2- 70 squares
$textbf{(d)}$ case 1- 56 squares
case 1- 56 squares
$textbf{(e)}$ This result makes sense as the final result here, can be obtained by mathematical multiplication of terms one after another.
For case 1 its multiplication by 0.2 followed by 0.3
For case 2 its multiplication by 0.3 followed by 0.2
Due to associative property of multiplication the result remained same.
sales tax is represented on the cost as
$$
text{tax}= xcdot dfrac{5}{100}
$$
Now, total cost after adding the sales tax will become
$$
text{total cost}= x+xcdot dfrac{5}{100}=xcdot dfrac{105}{100}=1.05x
$$
$textbf{(b)}$ If $x$ represent the cost of shirt and discount is 20% then
discount is represented on the cost as
$$
text{discount}= xcdot dfrac{20}{100}
$$
Now, total cost after the discount becomes
$$
text{total cost}= x-xcdot dfrac{20}{100}=xcdot dfrac{80}{100}=0.8x
$$
$textbf{(c)}$ Lets, find out the cost Trixie has to pay if tax is added first then discount is given later
Cost after tax addition is $1.05x$ and after 20% discount is given at this cost the
final value to pay becomes
$$
begin{align*}
&1.05x-1.05x cdot dfrac{20}{100}\
&=1.05x(1-0.2)\
&=1.05xtimes 0.8\
&=0.84x
end{align*}
$$
Also, lets find out the cost Trixie has to pay if discount is added first then tax is added later
Cost after discount is $0.8x$ and after 5% taxis added at this cost the then final value to pay becomes
$$
begin{align*}
&0.8x+0.8x cdot dfrac{5}{100}\
&=0.8x(1+0.05)\
&=0.8xtimes 1.05\
&=0.84x
end{align*}
$$
Therefore, Trixie has to pay the same amount for any of the cases.
$textbf{(b)}$ Discount$=xcdot dfrac{20}{100}$ and cost after discount is $0.8x$
$textbf{(c)}$ No, she didn’t get charged extra money.
Required equation for this situation will be the following:
$$
y=6(3)^{x-1}
$$
#### (b)
We will substitute $30$ million in the previous formula for $y$ and solve it for $x$ and get the following:
$$
30 000 000=6cdot(3)^{x-1}
$$
$$
3^{x-1}=5000000
$$
$$
x-1approx14
$$
$$
xapprox15
$$
So, it passed at least $15$ months.
Equation for this situation would be the following:
$$
y=6(0.3)^{x-1}
$$
We will substitute $100$ for $y$ and solve the equation for $x$ and get the following:
$$
100=6(0.3)^{x-1}
$$
$$
(0.3)^{x-1}=16.67
$$
$$
x-1=-2.34
$$
$$
x=-1.34
$$
Because we got negative number, and in this situation it is not possible, so, the conclusion is that never be less than $100$ rabbits.
$textbf{(a)}$ 3% increase
$$
begin{align*}
&x+xcdot dfrac{3}{100}tag{take $x$ common}\
&=x(1+dfrac{3}{100})\
&=x(dfrac{100+3}{100})\
&=x(dfrac{103}{100})\
&=x(1.03)
end{align*}
$$
With 3% increase the starting term $x$ changes to $1.03x$, hence the multiplier is $boxed{1.03}$
$textbf{(b)}$ 25% decrease
$$
begin{align*}
&x-xcdot dfrac{25}{100}tag{take $x$ common}\
&=x(1-dfrac{25}{100})\
&=x(dfrac{100-25}{100})\
&=x(dfrac{75}{100})\
&=x(0.75)
end{align*}
$$
With 25% decrease the starting term $x$ changes to $0.75x$, hence the multiplier is $boxed{0.75}$
$$
begin{align*}
&x-xcdot dfrac{13}{100}tag{take $x$ common}\
&=x(1-dfrac{13}{100})\
&=x(dfrac{100-13}{100})\
&=x(dfrac{87}{100})\
&=x(0.87)
end{align*}
$$
With 13% decrease the starting term $x$ changes to $0.87x$, hence the multiplier is $boxed{0.87}$
$textbf{(d)}$ 2.08% increase
$$
begin{align*}
&x+xcdot dfrac{2.08}{100}tag{take $x$ common}\
&=x(1+dfrac{2.08}{100})\
&=x(dfrac{100+2.08}{100})\
&=x(dfrac{102.08}{100})\
&=x(1.0208)
end{align*}
$$
With 2.08% increase the starting term $x$ changes to $1.0208x$, hence the multiplier is $boxed{1.0208}$
$textbf{(b)}$ $0.75$
$textbf{(c)}$ $0.87$
$textbf{(d)}$ $1.0208$
textbf{(a)}
$$
#1
For the given sequence each term can be represented as by $t(n+1)=t(n)+d$, hence its an arithmetic sequence with $t(0)=16$ and the common difference $d=-3$
#2
Its neither Arithmetic nor Geometric sequence. this is because the sequence is decreasing for some terms then starts increasing which is not possible with any of arithmetic or geometric sequence as either they will keep on increasing or keep on decreasing.
#3
Given sequence is the Geometric with common ratio$=dfrac{t(n+1)}{t(n)}=dfrac{8}{4}=2$
$$
textbf{(b)}
$$
#1
General term of an arithmetic sequence is given by $t(n)=t(0)+(n-1)d$
$Rightarrow$
$$
t(n)=16+(n-1)cdot -3
$$
#3
General term of an geometric sequence is given by $t(n)=ar^{n-1}$
$Rightarrow$
$$
t(n)=16cdot 2^{n-1}
$$
$textbf{(b)}$
$$
t(n)=16+(n-1)cdot -3
$$
$$
t(n)=16cdot 2^{n-1}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Therefore, the equation of a line of slope $-dfrac{1}{3}$ passing through a point $(9,-1)$ is given by
$$
begin{align*}
y-(-1)&=-dfrac{1}{3}cdot (x-9)\
y+1&=-dfrac{1}{3}cdot x -dfrac{1}{3}cdot (-9)\
y+1&=-dfrac{1}{3}cdot x+3\
y&=-dfrac{1}{3}cdot x+3-1\
&boxed{y=-dfrac{1}{3}cdot x+2}
end{align*}
$$
y=-dfrac{1}{3}cdot x+2
$$
$$
begin{align*}
8-(2x+1)&=3tag{use distributive property}\
8-2x-1&=3\
7-2x&=3tag{subtract 7 from each side}\
7-7-2x&=3-7\
-2x&=-4tag{divide each side by -2}\
dfrac{-2x}{-2}&=dfrac{-4}{-2}\
&boxed{x=2}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
sqrt{x}+4&=9tag{subtract 4 from each side}\
sqrt{x}+4-4&=9-4\
sqrt{x}&=5tag{squaring both side}\
(sqrt{x})^2&=5^2\
x&=25\
&boxed{x=25}
end{align*}
$$
$textbf{(b)}$ $x=25$
We can also make scatterplot for the given data and determine the line of best fit. A line of best fit with lower magnitude of residual signifies a better linear association between the parameters.
$textbf{(b)}$ The electronically calculated value of correlation coefficient $r$ and the scatterplot along with the line of best fit is attached below.
The value of $r$ is $-0.928$ which is very close to $-1$ which signifies that there is strong negative linear association between Length of Organelle and the Diameter of cell which means with the increase in the length of the organelle the diameter of the cell will decrease.
We can also observe the scatterplot and the line of best fit on it. The equation of line of best fit is $y=-1.604x+49.497$ and we can see that the residuals are relatively small hence, it represents a good linear association.
$textbf{(b)}$ The value of correlation coefficient is calculated for the given case which is $r=-0.9281$ and the scatterplot along with the line of best fit is attached inside.
$$
Rightarrow
$$
$$
begin{align*}
t(0)&=100\
t(1)&=dfrac{100}{2}=50\
t(2)&=dfrac{50}{2}=25\
t(3)&=dfrac{25}{2}=12.5\
t(4)&=dfrac{12.5}{2}=6.25\
t(5)&=dfrac{6.25}{2}=3.125\
t(6)&=dfrac{3.125}{2}=1.5625\
t(7)&=dfrac{1.5625}{2}=0.78125
end{align*}
$$
The distance after 7 times walking and 7 minutes waiting between him and the door becomes $0.78125$. The distance will keep getting half every time but will never become 0 as it will constitute a small value after every time of walking. This means theoretically there will always be a minute distance between him and the door. And hence, he will only reach the door after infinite time.
Other way to prove that is, we can represent his distance from the door in the form of general term which is given by
$$
t(n)=100cdot(dfrac{1}{2})^n
$$
We can see that $t(n)$ will become 0 only when value of $n$ tends to $infty$
$Rightarrow$
$$
text{speed}=dfrac{4}{45} dfrac{text{miles}}{text{minute}}
$$
Now, time taken by him to cover 10 miles can be found out by dividing the distance by his speed.
$$
text{time}=dfrac{text{distance}}{text{speed}}=dfrac{10}{(4/45)}=dfrac{45cdot 10}{4}=112.5 text{ minutes}
$$
For his unit rate in miles per hour we need to covert given time in hours first. We know that 60 minutes is equal to 1 hour. This implies that 45 minutes is $dfrac{45}{60}=dfrac{3}{4}$ hours. So , we can say that Zeke ran 4 miles in $dfrac{3}{4}$ hours.So we can find his speed in miles per hour by dividing 4 miles by $dfrac{3}{4}$ hours.
$Rightarrow$
$$
text{speed}=dfrac{4}{frac{3}{4}}=dfrac{16}{3}=5.333
dfrac{text{miles}}{text{hour}}
$$
dfrac{text{miles}}{text{hour}}$
$bullet$ Sequence 1.
$$
d=6-2=4
$$
$$
boxed{t(n)=2+(n-1)4}
$$
$$
begin{align*}
t(3)&=2+(3-1)4tag{term 3rd}\
t(3)&=2+(2)4\
t(3)&=10\
t(4)&=2+(4-1)4tag{term $4^text{th}$}\
t(4)&=2+(3)4\
t(4)&=14\
t(5)&=2+(5-1)4tag{term $5^text{th}$}\
t(5)&=2+(4)4\
t(5)&=18\
t(6)&=2+(6-1)4tag{term $6^text{th}$}\
t(6)&=2+(5)4\
t(6)&=22\
end{align*}
$$
$$
d=12-24=-12
$$
$$
boxed{t(n)=24+(n-1)(-12)}
$$
$$
begin{align*}
t(3)&=24+(3-1)(-12)tag{term 3rd}\
t(3)&=24+(2)(-12)\
t(3)&=0\
t(4)&=24+(4-1)(-12)tag{term $4^text{th}$}\
t(4)&=24+(3)(-12)\
t(4)&=-12\
t(5)&=24+(5-1)(-12)tag{term $5^text{th}$}\
t(5)&=24+(4)(-12)\
t(5)&=-24\
t(6)&=24+(6-1)(-12)tag{term $6^text{th}$}\
t(6)&=24+(5)(-12)\
t(6)&=-36\
end{align*}
$$
$bullet$ Sequence 3.
$$
d=5-1=4
$$
$$
boxed{t(n)=1+(n-1)4}
$$
$$
begin{align*}
t(3)&=1+(3-1)4=9tag{term 3rd}\
t(4)&=1+(4-1)4=13tag{term $4^text{th}$}\
t(5)&=1+(5-1)4=17tag{term $5^text{th}$}\
t(6)&=1+(6-1)4=21tag{term $6^text{th}$}\
end{align*}
$$
The general term for a geometric sequence is given by $t(n)=t(1)r^{n-1}$ where $r$ represents the common ratio which can be found by dividing two consecutive terms such that a term with higher term number is divided by the term with lower term number.
$bullet$ sequence 1.
$$
r=dfrac{t(2)}{t(1)}=dfrac{6}{2}=3
$$
$$
boxed{t(n)=2(3^{n-1})}
$$
$$
begin{align*}
t(3)&=2(3^{3-1})=2(9)=18tag{term 3rd}\
t(4)&=2(3^{4-1})=2(27)=54tag{term $4^text{th}$}\
t(5)&=2(3^{5-1})=2(81)=162tag{term $5^text{th}$}\
t(6)&=2(3^{6-1})=2(243)=486tag{term $6^text{th}$}\
end{align*}
$$
$bullet$ sequence 2.
$$
r=dfrac{t(2)}{t(1)}=dfrac{12}{24}=dfrac{1}{2}
$$
$$
boxed{t(n)=24cdot(dfrac{1}{2})^{n-1}}
$$
$$
begin{align*}
t(3)&=24cdot(dfrac{1}{2})^{3-1}=24(dfrac{1}{4})=6tag{term 3rd}\
t(4)&=24cdot(dfrac{1}{2})^{4-1}=24(dfrac{1}{8})=3tag{term $4^text{th}$}\
t(5)&=24cdot(dfrac{1}{2})^{5-1}=24(dfrac{1}{16})=1.5tag{term $5^text{th}$}\
t(6)&=24cdot(dfrac{1}{2})^{65-1}=24(dfrac{1}{32})=0.75tag{term $6^text{th}$}\
end{align*}
$$
$$
r=dfrac{t(2)}{t(1)}=dfrac{5}{1}=5
$$
$$
boxed{t(n)=1(5^{n-1})}
$$
$$
begin{align*}
t(3)&=1(5^{3-1})=25tag{term 3rd}\
t(4)&=1(5^{4-1})=125tag{term $4^text{th}$}\
t(5)&=1(5^{5-1})=625tag{term $5^text{th}$}\
t(6)&=1(5^{6-1})=3125tag{term $6^text{th}$}
end{align*}
$$
$textbf{(c)}$
$bullet$ sequence 1.
$$
t(n)=1+5^{n-1}
$$
$bullet$ sequence 2.
$$
t(n)=25-13^{n-1}
$$
$bullet$ sequence 3.
$$
t(n)=6^{n-1}-2^{n-1}+1
$$
General term of an Geometric sequence is given by $t(n)=t(1)cdot r^{n-1}$ , so for part (b) we can try to write the sequences in this form and then we can solve for the value of next term by putting different values of $n$ in it.
The complete explanation of each part is included inside.
$t_{1}(n)=-2+4n$
$t_{2}(n)=36-12n$
$t_{3}(n)=-3+4n$
a1=2, d1=4
a2=24, d2=-12
a3=1, d3=4
Next four numbers would be formed by adding ‘d’ to the respective ‘a’s.
2,6,10,14,18,22….
24,12,0,-12,-24,-36……
1,5,9,13,17,21…….
$t_{1}(n)=2*3^{n-1}$
$t_{2}(n)=24*0.5^{n-1}$
$t_{3}(n)=1*5^{n-1}$
a1=2, r1=3
a2=24, r2=0.5
a3=1, r3=5
Next four numbers would be formed by multipying ‘r’ to the respective ‘a’s.
2,6,18,54,162,486….
24,12,6,3,1.5,0.75……
1,5,25,125,625,3125…….
$t_{2}(n+1)=t_{2}(n)*0.25+6$ where $t_{2}(1)=24$
$t_{3}(n+1)=t_{3}(n)*3+2$ where $t_{3}(1)=1$
24, 24/4+6=12, 12/4+6=9, 9/4+6=8.25 and so on
1, 1*3+2=5, 5*3+2=17, 17*3+2=53 and so on
$$
begin{align*}
(x+2)(x+3)&=x^2-10tag{use distributive property}\
x(x+3)+2(x+3)&=x^2-10tag{solve brackets}\
xcdot x+xcdot 3+2cdot x+2cdot 3&=x^2-10\
x^2+3x+2x+6&=x^2-10tag{subtract $x^2$ from each side}\
x^2-x^2+5x+6&=x^2-x^2-10\
5x+6&=-10tag{subtract 6 from each side}\
5x+6-6&=-10-6\
5x&=-16tag{divide each side by 5}\
dfrac{5x}{5}&=dfrac{-16}{5}\
&boxed{x=dfrac{-16}{5}}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
dfrac{1}{2}x+dfrac{1}{3}x-7&=dfrac{5}{6}xtag{multiply each term by 6 (LCM) }\
dfrac{1}{2}xcdot 6+dfrac{1}{3}xcdot 6-7cdot 6&=dfrac{5}{6}xcdot 6\
3x+2x-42&=5x\
5x-42&=5xtag{subtract $5x$ from each side}\
5x-5x-42&=5x-5x\
-42&=0tag{not true}
end{align*}
$$
Therefore, equation $dfrac{1}{2}x+dfrac{1}{3}x-7=dfrac{5}{6}x$ has no solution.
$$
begin{align*}
dfrac{x+1}{3}&=dfrac{x}{2}tag{multiply each side by 6 (LCM)}\
dfrac{x+1}{3}cdot 6&=dfrac{x}{2}cdot 6\
dfrac{6}{3}(x+1)&=dfrac{6}{2}(x)\
2(x+1)&=3(x)\
2x+2&=3xtag{subtract 2x from each side}\
2x-2x+2&=3x-2x\
2&=x\
&boxed{x=2}
end{align*}
$$
$textbf{(d)}$
$$
begin{align*}
9^x&=(dfrac{1}{3})^{x+3}tag{rewrite 9 as $3^2$}\
(3^2)^x&=(dfrac{1}{3})^{x+3}tag{use $(a^m)^n=a^{mcdot n}$}\
3^{2x}&=dfrac{1^{x+3}}{3^{x+3}}\
3^{2x}&=dfrac{1}{3^{x+3}}tag{use $dfrac{1}{a^m}=a^{-m}$}\
3^{2x}&=3^{-1cdot (x+3)}tag{equate the powers, as base is same}\
Rightarrow\
2x&=-x-3tag{add $x$ to the each side}\
2x+x&=-x+x-3\
3x&=-3tag{divide each side by 3}\
dfrac{3x}{3}&=dfrac{-3}{3}\
&boxed{x=-1}
end{align*}
$$
$textbf{(b)}$ No solution
$textbf{(c)}$ $x=2$
$textbf{(d)}$ $x=-1$
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by
$$
y-y_1=mcdot (x-x_1)
$$
Now, we have given points as $(0,-3)$ and $(-9,-9)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{-9-(-3)}{-9-0}\\
&=dfrac{-9+3}{-9}\
&=dfrac{2}{3}
end{align*}
$$
Now, the equation of a line of slope $dfrac{2}{3}$ passing through a point $(0,-3)$ is given by
$$
begin{align*}
y-(-3)&=dfrac{2}{3}cdot (x-0)\
y+3&=dfrac{2}{3}cdot x\
y&=dfrac{2}{3}cdot x-3
end{align*}
$$
y=dfrac{2}{3}cdot x-3
$$
$$
begin{align*}
f(x)&=dfrac{1}{x+2}\
f(-3)&=dfrac{1}{(-3)+2}\
f(-3)&=dfrac{1}{-1}\
f(-3)&=-1\
&boxed{f(-3)=-1}
end{align*}
$$
$textbf{(b)}$
$$
begin{align*}
f(x)&=dfrac{1}{x+2}\
f(-1.5)&=dfrac{1}{(-1.5)+2}\
f(-1.5)&=dfrac{1}{0.5}\
f(-1.5)&=dfrac{1}{5/10}\
f(-1.5)&=dfrac{1cdot 10}{5}\
f(-1.5)&=2\
&boxed{f(-1.5)=2}
end{align*}
$$
$$
begin{align*}
f(x)&=dfrac{1}{x+2}\
f(-2)&=dfrac{1}{(-2)+2}\
f(-3)&=dfrac{1}{0}tag{$dfrac{a}{0}$ is not defined}
end{align*}
$$
Any number divide by 0 is not defined,therefore, $f(-2)$ is not defined.
$textbf{(d)}$
$$
begin{align*}
f(x)&=dfrac{1}{x+2}\
(5)&=dfrac{1}{x+2}tag{multiply each side by $x+2$}\
5cdot (x+2)&=dfrac{1}{x+2}cdot (x+2)\
5(x+2)&=1tag{solve bracket}\
5x+10&=1tag{subtract 10 from each side}\
5x+10-10&=1-10\
5x&=-9tag{divide each side by 5}\
dfrac{5x}{5}&=dfrac{-9}{5}\
x&=dfrac{-9}{5}\
boxed{x=dfrac{-9}{5}}
end{align*}
$$
$textbf{(b)}$ $2$
$textbf{(c)}$ Not defined
$textbf{(d)}$ $dfrac{-9}{5}$
$$
text{Area}=l^2 text{ } text{ units}^2
$$
We are given a square with side length 7 cm, therefore the area of this square is
$$
begin{align*}
text{Area}&=7^2=49 text{cm}^2
end{align*}
$$
$textbf{(b)}$ Area of any triangle is given by the formula shown below
$$
text{Area}=dfrac{1}{2}times text{base}times text{ perpendicular height}
$$
For the given triangle we have base length $=10$ inches and perpendicular height $=4$ inches.
Hence, the area of the given triangle is
$$
text{Area}=dfrac{1}{2}times 10 times 4=20 text{ inches}^2
$$
$textbf{(c)}$ The area of the given trapezium can be calculated by dividing it into parts. These parts consists 3 parts which are
$bullet$A triangle with base 6 units and perpendicular height 6 units
$Rightarrow$
$$
text{Area}_1=dfrac{1}{2}times 6 times 6=18 text{units}^2
$$
$bullet$A rectangle with length 8 units and breath 6 units
$Rightarrow$
$$
text{Area}_2= 8 times 6=48 text{units}^2
$$
$bullet$A triangle with base 2 units and perpendicular height 6 units
$Rightarrow$
$$
text{Area}_3=dfrac{1}{2}times 2 times 6=6 text{units}^2
$$
Therefore the total area of trapezium is summation of all the above three calculated areas.
Total area$= 18+48+6=72$units$^2$
$textbf{(b)}$ 20 inches$^2$
$textbf{(c)}$ 72 units$^2$
As we know that the general term $t(n)$ of an arithmetic sequence is given by $$t(n)=t(1)+(n-1)d$$
So, we can write its explicit equation as shown below.
$$boxed{t(n)=-5+(n-1)4}$$
The table of values and the graph is attached below.
begin{center}
begin{tabular}{|p{1.5cm}|p{1.5cm}|}
hline
n&t(n)\
hline
1&-5\
hline
2&-1\
hline
3&3\
hline
4&7\
hline
5&11\
hline
6&15\
hline
7&19\
hline
end{tabular}
end{center}
$$
begin{align*}
t(n)&=-5+(n-1)4\
400&=-5+(n-1)4tag{add 5 to the each side}\
400+5&=-5+5+(n-1)4\
405&=(n-1)4tag{divide each side by 4}\
dfrac{405}{4}&=dfrac{(n-1)4}{4}\
101.25&=n-1tag{add 1 to the each side}\
101.25+1&=n-1+1\
102.25&=n
end{align*}
$$
We can see, for the term 400 we did not got the term number an integer value. Therefore, 400 cannot be a term of the given sequence.
begin{align*}
f(x)&=4x-9\
f(-5)&=4(-5)-9\
f(-5)&=-20-9\
f(-5)&=-29\
f(-0.5)&=4(-0.5)-9\
f(-0.5)&=-2-9\
f(-0.5)&=-11\
f(0)&=4(0)-9\
f(0)&=-9\
f(1)&=4(1)-9\
f(1)&=4-9\
f(1)&=-5\
f(2.5)&=4(2..5)-9\
f(2.5)&=10-9\
f(2.5)&=1
end{align*}
So this can be represented as table, see the table attached below.\
begin{center}
begin{tabular}{|p{2cm}|p{3cm}|}
hline
x&f(x)\
hline
-5&-29\
hline
-0.5&-11\
hline
0&-9\
hline
1&-5\
hline
2.5&1\
hline
end{tabular}
end{center}
$textbf{(b)}$ No
$textbf{(c)}$ This is a continuous function and its table values and graph is attached inside.
$textbf{(d)}$ Yes, The function $f(x)=4x-9$ can take value 400 corresponding to $x=102.25$
But $t(n)=2cdot 3^n$ is a discrete function.These can only take natural numbers as its input because of the reason that each of its term is given a term number and a term number can never be negative or fractional.The output corresponding to only natural number as inputs will be discrete only and will not able to cover all real values of numbers as output. Hence, sequences are discrete function.
$textbf{(b)}$ We can equate the $t(n)$ equal to 1400 for the equation and try to find the value of $n$ corresponding to it. If this value belongs to integers then we can say it is possible for $t(n)$ to be equal to 1400 otherwise it is not.
This restriction is due to the reason that $t(n)$ can take only natural numbers in its domain.
$$
begin{align*}
t(n)&=2cdot 3^n\
1400&=2cdot 3^ntag{divide each side by 2}\
700&=3^ntag{taking log to the base 3 on both side}\
log_3{700}&=log_3{3^n}\
log_3{700}&=nlog_3{3}\
log_3{700}&=n(1)\
5.963&=n
end{align*}
$$
We can see that the input corresponding to $t(n)=1400$ is not integral. hence, $t(n)$ cannot take the value 1400.
$textbf{(d)}$ Functions and sequences are similar as these both are functions. But the difference between both is that function can take all real values as input and are continuous unless it becomes not defined at some point. whereas the sequences can take only natural number as input and can give only discrete value of output.
$f(x)=2cdot 3^x$ is a function but $t(n)=2cdot 3^n$ is a discrete function or sequence (more precisely).
$textbf{(b)}$ No, it can only take natural number as input.
$textbf{(c)}$ Yes
$textbf{(d)}$ Functions and sequences are similar as these both are functions. But the difference between both is that function can take all real values as input and are continuous unless it becomes not defined at some point. whereas the sequences can take only natural number as input and can give only discrete values of output.
Yes, sequences are also a function. But these are special type of functions. These can only take natural numbers as its input because of the reason that each of its term is given a term number and a term number can never be negative or fractional.
The output corresponding to only natural number as inputs will be discrete only and will not able to cover all real values of numbers as output. Hence, sequences are discrete function whereas a simple function is continuous and can take all real values as input unless it becomes not defined for some inputs.
A function is represented by $f(x)$ and takes $x$ as input whereas a sequence is represented by $t(n)$ which takes $n$ as input.
Sequences are discrete function whereas a simple function is continuous and can take all real values as input unless it becomes not defined for some inputs.
$$
begin{align*}
a_n&=dfrac{3}{2}n-1\
a_1&=dfrac{3}{2}(1)-1=dfrac{3}{2}-1=dfrac{3-2}{2}=dfrac{1}{2}\
a_2&=dfrac{3}{2}(2)-1=dfrac{2}{2}(3)-1=3-1=2\
a_3&=dfrac{3}{2}(3)-1=dfrac{9}{2}-1=dfrac{9-2}{2}=dfrac{7}{2}\
a_4&=dfrac{3}{2}(4)-1=dfrac{4}{2}(3)-1=2cdot3-1=5\
a_5&=dfrac{3}{2}(5)-1=dfrac{15}{2}-1=dfrac{15-2}{2}=dfrac{13}{2}
end{align*}
$$
Therefore, first five term are $(dfrac{1}{2}, 2, dfrac{7}{2}, 5, dfrac{13}{2}, cdots)$
$textbf{(b)}$
$$
begin{align*}
a_n&=dfrac{1}{4}(-8)^n\
a_1&=dfrac{1}{4}(-8)^1=dfrac{1}{4}(-8)=dfrac{-8}{4}=-2\
a_2&=dfrac{1}{4}(-8)^2=dfrac{1}{4}(64)=dfrac{64}{4}=16\
a_3&=dfrac{1}{4}(-8)^3=dfrac{1}{4}(-512)=dfrac{-512}{4}=-128\
end{align*}
$$
Therefore, first three term are $(-2, 16, -128, cdots)$
$$
a_n=a_1(r)^{n-1}
$$
where $a_1$ is the first term and $r$ is the common ratio of the sequence. we have $r=-1$ and $a=-4$ therefore, the equation becomes
$$
boxed{a_n=-4(-1)^{n-1}}
$$
$textbf{(d)}$ Given sequence is $(7, 13, 19, 25, cdots)$
We can see the common difference for this sequence is $d=13-7=6$, which means each next term of this sequence can be obtained by adding 6 to the previous term.
We know that the general term of an arithmetic progression is given by
$$
a_n=a_1+(n-1)d
$$
where, $a_n$ represents the $n^text{th}$ term of the sequence , $a_1$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
We can put the known value $a_1=7$ and $d=6$ in the general equation, the final equation becomes
$$
boxed{a_n=7+(n-1)6}
$$
$textbf{(b)}$ The first three term are $(-2, 16, -128, cdots)$
$textbf{(c)}$ $a_n=-4(-1)^{n-1}$
$textbf{(d)}$ $a_n=7+(n-1)6$
We are given that the output of $p(r)=2cdot 5^r$ is 78,000. On solving for the value of $r$ we get
$$
begin{align*}
78000&=2cdot 5^r\
39000&=5^r\
r&=6.569
end{align*}
$$
The given condition is possible for a value of $r=6.569$ which is not a natural number. Therefore, p(r) has real numbers in its domain and hence $p(r)$ cannot be a sequence.
By Equal Values Method, we can treat each side of the equation as two separate equations:
$$
begin{align*}
y&=200(0.5)^x\
y&=3.125
end{align*}
$$
Graph both equations on Y1 and Y2, adjust the window if necessary, then use the $textbf{intersect}$ feature to find the point of intersection of the graphs. The $x$-coordinate of the point of intersection is the solution of the equation. In this case,
$$
color{#c34632}x=6
$$
By Equal Values Method, we can treat each side of the equation as two separate equations:
$$
begin{align*}
y&=318\
y&=6cdot 3^x
end{align*}
$$
Graph both equations on Y1 and Y2, adjust the window if necessary, then use the $textbf{intersect}$ feature to find the point of intersection of the graphs. The $x$-coordinate of the point of intersection is the solution of the equation. In this case,
$$
color{#c34632}xapprox 3.61
$$
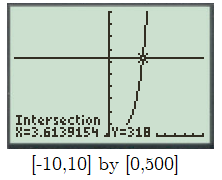
b. $xapprox 3.61$
$$
begin{align*}
200(0.5)^x&=3.125tag{divide each side by 200}\
dfrac{200(0.5)^x}{200}&=dfrac{3.125}{200}\
(0.5)^x&=0.015625tag{take log to the base 0.5 on the both side}\
log_{0.5}(0.5)^x&=log_{0.5}0.015625tag{use $ log_ab^m=m(log_ab)$}\
x(log_{0.5}0.5)&=6tag{use $log_aa=1$}\
xcdot 1&=6\
&boxed{x=6}
end{align*}
$$
$$
textbf{(b)}
$$
$$
begin{align*}
318&=6cdot 3^xtag{divide each side by 6}\
dfrac{318}{6}&=dfrac{6cdot 3^x}{6}\
53&=3^xtag{take log to the base 3 on the both side}\
log_353&=log_3(3)^xtag{use $log_ab^m=m(log_ab)$}\
log_353&=x(log_33)tag{use $log_aa=1$}\
3.6139&=xcdot 1\
&boxed{x=3.61}
end{align*}
$$
$textbf{(b)}$ $x=3.61$
$textbf{(a)}$ For the given function $f(x)=3x-5$ the input variable $x$ can take value from all real numbers. therefore, domain of this function is $(-infty,+infty)$
$textbf{(b)}$ For the given sequence $t(n)=3n-5$ the input variable $n$ can take only positive integral values. Therefore, domain of this sequence is all natural number $(1, 2, 3, cdots)$
$textbf{(c)}$ For the given function $f(x)=dfrac{5}{x}$ the input variable $x$ can take value from all real numbers except $x=0$ which makes the $f(x)$ not defined as $dfrac{5}{0}$ is not defined. Therefore, domain of this function is $(-infty,+infty)-(0)$
$textbf{(d)}$ For the given sequence $t(n)=dfrac{5}{n}$ the input variable $n$ can take only positive integral values. Therefore, domain of this sequence is all natural number $(1, 2, 3, cdots)$. The $n=0$ is already is not in its domain so we need not to worry about it.
$textbf{(b)}$ The domain of this sequence is all natural number $(1, 2, 3, cdots)$
$textbf{(c)}$ $(-infty,+infty)-(0)$
$textbf{(d)}$ The domain of this sequence is all natural number $(1, 2, 3, cdots)$
For this sequence to have a term with the value of 200, we should get the value of $n$ corresponding to it as a natural number.
$$
begin{align*}
200&= 5cdot 2^n\
40&=2^n\
n&=dfrac{log 40}{log 2}\
n&=5.322
end{align*}
$$
The value of $n=5.322$ doesn’t belong to a natural number for a value of $t(n)=200$ hence it is not possible for the sequence to have a term as 200.
$textbf{(b)}$ Function is given with the equation $f(x) =5cdot 2^x$. A function can have real numbers in its domain. Hence, value of $x=5.322$ belongs to real number for which $f(x)$ gives output 200. Therefore, it is possible for $f(x)$ to have an output 200.
$textbf{(b)}$ Yes, 200 can be the output of $f(x)$
Now, putting the values of $n$ into the general term of the sequence we can easily find $a_4$ and $a_5$ as shown below.
$textbf{(a)}a_4 =a_3+ 6 = 17 + 6 =23$
$textbf{(b)}a_5 =a_4+ 6 = 23 + 6 =29$
$textbf{(c)}$ First five terms of the sequence are $(5,11,17,23,29)$
$textbf{(b)}$ 29
$textbf{(c)}$ First five terms of the sequence are $(5,11,17,23,29)$
$$
x+y=775
$$
Therefore the distance ran by Ricardo can be found out by rearranging the above equation to write it in term of x
$Rightarrow$
$$
y=775-x
$$
$$
(2,6)text{ and }(5,15)
$$
We notice that the $y$-value is 3 times the $x$-value in both points. Since the pattern grows linearly, then the rule is:
$$
color{#c34632}y=3x
$$
We know that each figure is increased by constant number of tiles which is the common difference of the arithmetic sequence and is represented by $d$.
The difference between Figure 2 and Figure 5 will be of $3d$ which is equal to $15-6=9$ tiles. therefore, common difference $d=dfrac{9}{3}=3$
Now, Figure 1 will have 3 tiles less than the Figure 2 which means $t(1)=6-3=3$
We know that the general term of an arithmetic progression is given by
$$
t(n)=a+(n-1)d
$$
where, $t(n)$ represents the $n^text{th}$ term of the sequence , $a$ represents the first term of the sequence, $d$ represents the common difference (sequence generator) of the sequence and $n$ represents the term number.
putting the values of $d=3$ and $t(1)=a=3$ into the general equation we get the final equation as
$$
boxed{t(n)=3+(n-1)3}
$$
t(n)=3+(n-1)3
$$

