First of all, in order to get a box with a lid, there must be 6 pieces, so the net $c$ does not fit.

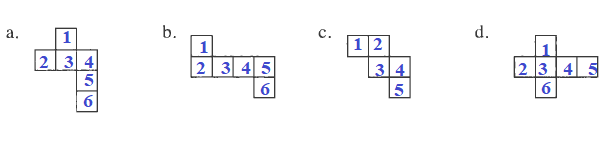
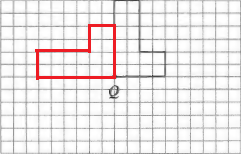
In net $a$ we can set side 1 to be the lid, sides 2, 3, 4 be lateral sides, side 5 the bottom, but side 6 overlaps side 2, therefore this net does not fit.

In net $b$, we can set side 1 as the lid, sides 2, 3, 4, 5 as lateral sides and side 6 as the bottom. Therefore this net fits.

In net $d$, we can set side 1 as the lid, sides 2, 3, 4, 5 as lateral sides and side 6 as the bottom. Therefore this net fits too.

Nets $b$ and $d$

When reflected,some of the letters change (letters $G, S, T, A, R, W$), others keep their form (letters $O, E$). The distance from the letter to the mirror is the same on both sides of the mirror.

c) What he sees after spinning the flag $180text{textdegree}$ around the pole is this:

For a motion to be a reflection the resultant figure should be laterally inverted and the distance of each point both on the object and image, from the line of reflection should be equal.

$textbf{(a)}$ This motion follows all the property of reflection mentioned above and hence its a reflection.

$textbf{(b)}$ This is not a reflection as the distance between a point on the object and the image is not equal from the line of reflection.

$textbf{(c)}$ Not a reflection as no lateral inversion.

$textbf{(d)}$ This motion follows all the property of reflection mentioned above and hence its a reflection.

$textbf{(a)}$ Reflection

$textbf{(b)}$ Not a reflection

$textbf{(c)}$ Not a reflection

$textbf{(d)}$ Reflection

$G(1,3)$

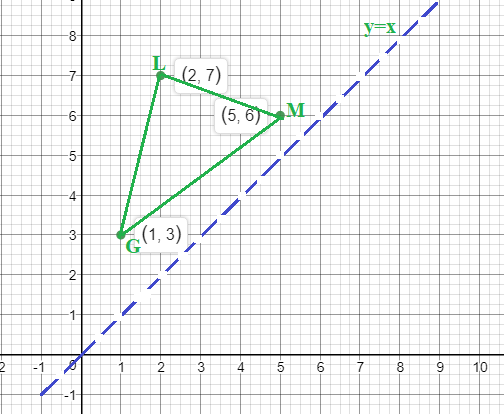
$L(2,7)$

$M(5,6)$

a)We graph $triangle GLM$:

b) We reflect the triangle across the line $y=x$:

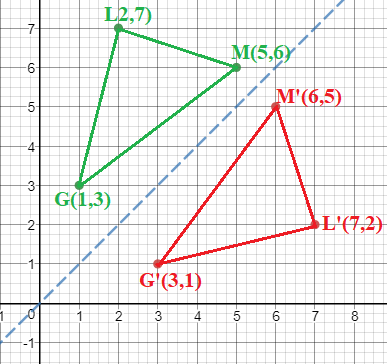
$$
(x,y)rightarrow(y,x)
$$

$$
(x,y)rightarrow(y,x)
$$

The equation of the refection line is $y=x$ and the coordinates change according to the rule:

For plotting a graph of the given equations of line, we need find the any two points on the each of the given equations , by choosing any one coordinate first then solving for the other coordinate. After we have 2 points then we can draw these points on the graph and then we can easily draw a line passing between these 2 points.\ Starting by $y$-intercept and $x$-intercept can be easier to find points on the line. Table for points on each the line is attached below.\\
textbf{(a)} $f(x) = 3x – 3 $\\ begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}| }
hline
$x$ & 0 & 1 \
hline
$f(x)$ & -3&0 \
hline
end{tabular}\\\\
textbf{(b)} $f(x)=-dfrac{2}{3}x +3$\\ begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}| }
hline
$x$ & 0 & 4.5 \
hline
$f(x)$ & 3&0 \
hline
end{tabular}\\\\
textbf{(c)} $f( x) = -4x + 5$\\ begin{tabular}{ |p{1cm}|p{1cm}|p{1cm}| }
hline
$x$ & 0 & 2 \
hline
$f(x)$ & 5&-3 \
hline
end{tabular}\\
Now, using these points in the respective tables , we can draw the lines on the graph, as shown in the graph attached below.

For plotting a graph of the given equations of line, we need find the any two points on the each of the given equations , by choosing any one coordinate first then solving for the other coordinate. After we have 2 points then we can draw these points on the graph and then we can easily draw a line passing between these 2 points.
Starting by $y$-intercept and $x$-intercept can be easier to find points on the line. See inside for the explanation and graph.

Given:

$$
AC=67 ; miles
$$

$$
AB=5x-2
$$

$$
BC=2x+6
$$

$$
AC=AB+BC
$$

$$
67=5x-2+2x+6
$$

$$
67=7x+4
$$

$$
67-4=7x
$$

$$
63=7x
$$

$$
x=9
$$

So, $AB=5 cdot 9-2=45-2=43$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=frac{97}{9}+left(-frac{29}{3}right)\\
& =frac{97}{9}-frac{29}{3} tag{Remove parentheses} \
&=frac{97}{9}-frac{29cdot :3}{9} tag{Adjust fractions} \
&=frac{97-29cdot :3}{9} \
&=frac{10}{9} tag{Multiply the numbers}\\
&=boxed{{color{#c34632} 1frac{1}{9} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
text{}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{107}{10}-frac{13}{5}\\
&=-frac{107}{10}-frac{13cdot :2}{10} tag{Adjust fractions} \
&=frac{-107-13cdot :2}{10}\
&=frac{-133}{10} \
&=-frac{133}{10}\\
&=boxed{{color{#c34632} -13frac{3}{10} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} text{} mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=left(frac{9}{2}right)left(-frac{33}{10}right)\\
& =-frac{9}{2}cdot frac{33}{10}tag{Remove parentheses} \
&=-frac{9cdot :33}{2cdot :10} tag{Multiply the numbers} \
&=-frac{297}{20} tag{Multiply the numbers}\\
&=boxed{{color{#c34632} -14frac{17}{20} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Multiply:fractions}:quad frac{a}{b}cdot frac{c}{d}=frac{a:cdot :c}{b:cdot :d}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{43}{5}div frac{6}{5}\\
& =-frac{43cdot :5}{5cdot :6} tag{Divide fractions } \
&=-frac{43}{6} tag{Cancel the common factor} \\
&=boxed{{color{#c34632} -7frac{1}{6} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Divide:fractions}:quad frac{frac{a}{b}}{frac{c}{d}}=frac{acdot :d}{bcdot :c}
$$

$$
text{}
$$

$$
color{#4257b2} text{a)} 1frac{1}{9}
$$

$$
color{#4257b2} text{b)} -13frac{3}{10}
$$

$$
color{#4257b2} text{c)} -14frac{17}{20}
$$

$$
color{#4257b2} text{d)} -7frac{1}{6}
$$

(a) To plot the data of the table, We have to use the ordered pairs from the table to plot points and then we draw the best fit line between the points.

The ordered pairs $color{#4257b2} (2, 73), (4, 63), (0, 89), (2, 85), (1, 90), (7, 58), (0, 97), (1, 90), (3, 79)$ and $color{#4257b2} (6, 41)$, Where the $x$ coordinates represent the tired behaviors during Professor Saksunn’s math class in a week and the $y$ coordinates represent the test score.

To get the equation of the plotted best fit line, We have to get two points on the line and from their coordinates we’ll get the equation of the line.

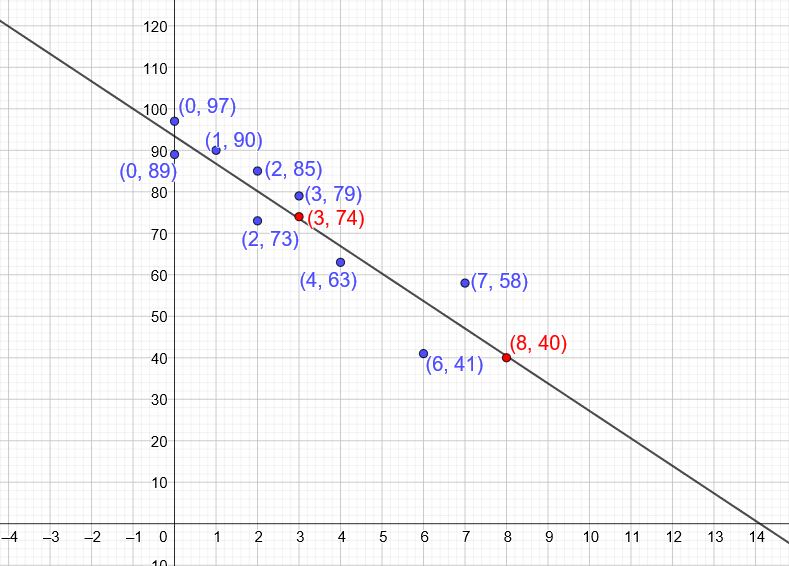
We can use the two points $color{#4257b2} (3, 74)$ and $color{#4257b2} (8, 40)$ which lie on the best fit line.

For the two points, $Delta y = 40-74= -34, Delta x = 8-3 = 5$

At first, We need the get the slope $m= dfrac{ Delta y}{ Delta x}$ $color{#4257b2} = dfrac{-34}{5} = – 6.8$

To get the equation of the line in the form $color{#c34632} y=mx+b$, We need to get the term $b$.

To get the term $b$, We substitute with the value of the slope and using anyone of the two points coorsinates in the equation above.

Using $(8, 40)$ $Rightarrow 40 = 8(-6.8)+b Rightarrow 40 = -54.4 +b Rightarrow b= 40+ 54.4 = 94.4$

The equation of the best fit line is $color{#c34632} y= -6.8x +94.4$

(b) We need to get the test score of a student that exhibits $5$ tired behaviors using the estimated equation.

We substitute with $color{#4257b2} x=5$ in the equation $y= -6.8x+ 94.4$ to get the value of $y$.

$$
Rightarrow y= -6.8(5)+94.4= 60.4 approx color{#c34632}boxed{60}
$$

(a)$y= -6.8x+94.4$

(b) $60$

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Now, we have given points as $(2,9)$ and $(4,16)$. Let $(x_1,y_1)=(2,9)$ and $(x_2,y_2)=(4,16)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{16-9}{4-2}\
&=dfrac{7}{2}
end{align*}
$$

Now, the equation of a line of slope $dfrac{7}{2}$ passing through a point $(2,9)$ is given by

$$
begin{align*}
y-(9)&=dfrac{7}{2}cdot (x-2)\
y-9&=dfrac{7}{2}cdot x +dfrac{7}{2}cdot (-2)\
y-9&=dfrac{7}{2}cdot x -7\
y&=dfrac{7}{2}cdot x -7+9\
y&=dfrac{7}{2}cdot x +2\
end{align*}
$$

$$
y=dfrac{7}{2}cdot x +2
$$

b) Translation moves each point of the original image to a new position by the same distance unlike reflection which, even if it preserves the original shape of the image, it does not move all points at the same distance. Therefore, except for some particular cases (for example equilateral triangle with one of the sides perpendicular on the reflection line), reflection doesn’t lead to the original image. In our case $triangle A”B”C”$ has been translated, but $triangle A’B’C’$ hasn’t.

a) We reflect $triangle EFG$ over line$v$ to from $triangle E’F’G’$ and then $triangle E’F’G’$ over line $w$ to form $triangle E”F”G”$.

$triangle E”F”G”$ is not a translation of the original triangle. It looks like the original triangle was rotated by $90text{textdegree}$.

b) We check the fact that $triangle E”F”G”$ is a figure obtained by rotation around the intersection point $P$ of the two reflection lines by using tracing paper.

c) We can get the same $triangle E”F”G”$ result if we rotate $triangle EFG$ $270text{textdegree}$ counterclockwise.

e) We rotate the polygon $90text{textdegree}$ counterclockwise around point $Q$:

a) We can reflect the square $ABCD$ across the vertical line situated at half the distance between the two squares:

b) We rotate the square $180text{textdegree}$ about the given point:

$textbf{(a)}$ Transformation is a broad word which can be anything like $textbf{Reflection}$, $textbf{Rotation}$ and even $textbf{Translation}$. But translation is just a type of transformation which means shifting of coordinates of a figure.

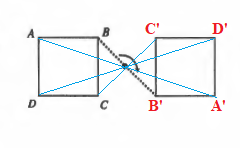
$textbf{(b)}$ There can be multiple ways to transform $Delta ABC$ into $Delta A’B’C’$

One way can be taking reflection of $Delta ABC$ along the line $x=3$ and then translating the image 2 units downwards.
Other way is first translating the $Delta ABC$ by 2 units, following by the reflection along the line $x=3$

$textbf{(c)}$ There is always multiple ways to describe a transform. For example a simple reflection can be achieved via three steps including a rotation and then reflection and again rotation to obtain the similar figure. but this can be time consuming and non-feasible.

$textbf{(a)}$ Transformation can be $textbf{Reflection}$, $textbf{Rotation}$ and even $textbf{Translation}$. But translation is a type of transformation which means shifting of coordinates of a figure.

$textbf{(b)}$ Reflection followed by translation or via translation followed by reflection

$textbf{(c)}$ Yes, there can always be multiple ways to describe a transformation.

$text{color{#c34632}(a)}$ According rigid transformations, the area of the image would always have the same area as the original polygon.

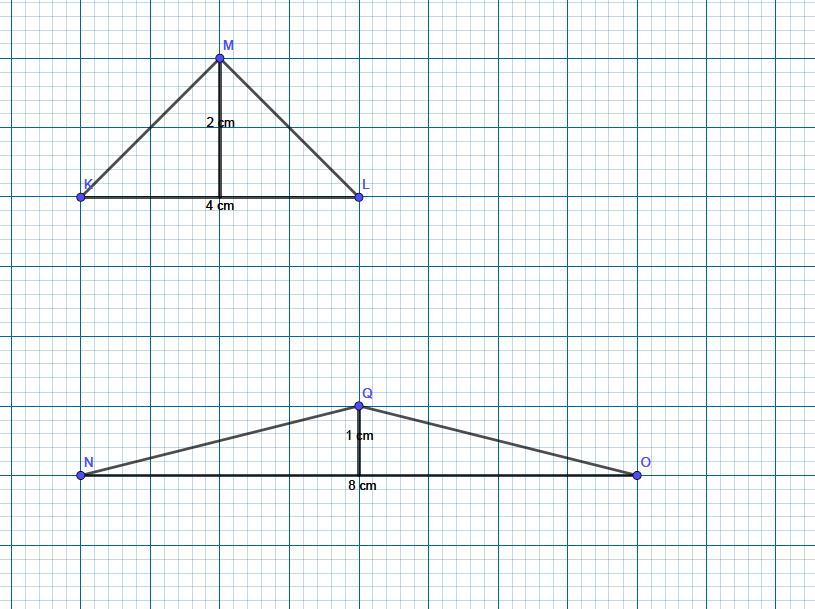
$text{color{#c34632}(b)}$ No, if two polygons have the same area that does’t mean that they always are the image of a series of rigid transformations.

for example: calculate the area of the two shown triangle ( Area $=dfrac{1}{2} times$ Base $times$ Height)

For triangle MLK, the base $= 4 cm$ and the height $=2 cm$

$color{#4257b2}Rightarrow A= dfrac{1}{2} times 4 times 2 = 4 cm^2$

For triangle QON, the base $= 8 cm$ and the height $=1 cm$

$color{#4257b2} Rightarrow A= dfrac{1}{2} times 8 times 1 = 4 cm^2$

As estimated the two shown triangles have the same area but the lengths of each one is different from the another one, So they are not the image of a series of rigid transformations.

$text{color{#c34632}(c)}$ For the triangle GEF, the base $= 8$ unit length and the height $=3$ unit length

$color{#4257b2} Rightarrow A= dfrac{1}{2} times 8 times 3 = 24$ unit area.

For the triangle of the image G”E”F”, the base $= 8$ unit length and the height $=3$ unit length

$color{#4257b2} Rightarrow A= dfrac{1}{2} times 8 times 3 = 24$ unit area.

The area of the triangle GEF is the same area of the triangle of the image G”E”F” and so that the area of the L shape shown in the figure and its image because the original L shape polygon and its image both have the same dimensions.

The area of the image of any polygon is the same area of the original polygon.

(a) Yes

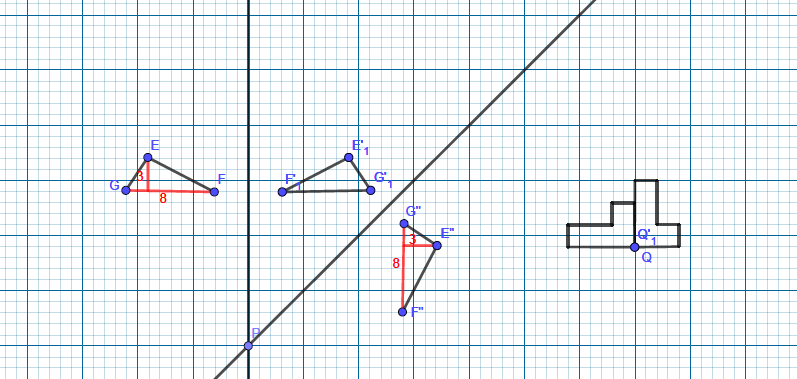
(b) No

(c) $24$ unit area

$textbf{(a)}$ Reflection

$textbf{(b)}$ Translation

$textbf{(c)}$ Rotation

$textbf{(d)}$ Rotation

$textbf{(e)}$ Reflection

$textbf{(f)}$ It is not possible to obtain such pair of polygon using a single transformation. This could be obtained by reflection followed by rotation or rotation followed by reflection.

$textbf{(a)}$ Slope of line passing through 2 given points $(x_1,y_1)$ and $(x_2,y_2)$ can be written as

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

Now, we have points as $(1,1)$ and $(2,4)$

$Rightarrow$
$$
begin{align*}
text{slope}&=dfrac{4-1}{2-1}\
&=dfrac{3}{1}\
&=3
end{align*}
$$

$textbf{(b)}$ y-intercept from the graph is -2

$textbf{(c)}$ Equation of line having a slope 3 and passing through (1,1) is

$$
begin{align*}
y-1&=3cdot (x-1)\
y&=3x-3+1\
y&=3x-2
end{align*}
$$

$textbf{(a)}$ 3

$textbf{(b)}$ -2

$textbf{(c)}$ $y=3x-2$

Using $alpha+beta=90text{textdegree}$ in complementary angles and

$alpha+beta=180text{textdegree}$ in supplementary angles

a) This angles are complementary, so

$$
6x+4x+10text{textdegree}=90text{textdegree}
$$

$$
10x+10text{textdegree}=90text{textdegree}
$$

$$
10x=80text{textdegree}
$$

$$
x=8text{textdegree}
$$

b) This angles are supplementary, so

$$
5x+13text{textdegree}+3x+7text{textdegree}=180text{textdegree}
$$

$$
8x+20text{textdegree}=180text{textdegree}
$$

$$
8x=160text{textdegree}
$$

$$
x=20text{textdegree}
$$

Domain of a relation or a function is the set of values of input variable $x$, for which it is defined. Range is the the set of values of output variable $y$ which it can give.

$textbf{(a)}$ Domain: All real numbers

Range: ($-infty$, 1]

$textbf{(b)}$ Domain: [-3, $infty$)

Range: [-2, $infty$)

$textbf{(c)}$ Domain: All real numbers

Range: ($-infty$, 0]

$textbf{(d)}$ Domain: All real numbers

Range: [-1, $infty$)

$textbf{(a)}$ Domain: All real numbers

Range: ($-infty$, 1]

$textbf{(b)}$ Domain: [-3, $infty$)

Range: [-2, $infty$)

$textbf{(c)}$ Domain: All real numbers

Range: ($-infty$, 0]

$textbf{(d)}$ Domain: All real numbers

Range: [-1, $infty$)

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{47}{6}+left(-frac{29}{4}right)\\
& =-frac{47}{6}-frac{29}{4} tag{Remove parentheses} \
&=-frac{47cdot :2}{12}-frac{29cdot :3}{12} tag{Adjust fractions} \
&=frac{-47cdot :2-29cdot :3}{12} \
&=frac{-181}{12}\
&=-frac{181}{12}\\
&=boxed{{color{#c34632} -15frac{1}{12} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{17}{2}-left(-frac{13}{4}right)\\
& =-frac{17}{2}+frac{13}{4} \
&=-frac{17cdot :2}{4}+frac{13}{4} tag{Adjust fractions} \
&=frac{-17cdot :2+13}{4} \
&=frac{-21}{4}\
&=-frac{21}{4}\\
&=boxed{{color{#c34632} -5frac{1}{4} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=left(-frac{17}{7}right)left(-7right)\\
& =frac{17}{7}cdot :7 tag{Remove parentheses} \
&=frac{17cdot :7}{7} tag{Multiply fractions} \\
&=boxed{{color{#c34632} 17 } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Multiply:fractions}:quad :acdot frac{b}{c}=frac{a:cdot :b}{c}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{17}{8}div frac{1}{5}\\
& =-frac{17cdot :5}{8cdot :1} tag{Divide fractions} \
&=-frac{85}{8} tag{Multiply the numbers} \\
&=boxed{{color{#c34632} -10frac{5}{8} } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Divide:fractions}:quad frac{frac{a}{b}}{frac{c}{d}}=frac{acdot :d}{bcdot :c}
$$

$$
text{a)} -15frac{1}{12}
$$

$$
text{b)} -5frac{1}{4}
$$

$$
text{c)} 17
$$

$$
text{d)} -10frac{5}{8}
$$

Using

$$
a^m cdot a^n=a^{m+n}
$$

$$
dfrac{a^m}{a^n}=a^{m-n}
$$

$$
(a^m)^n=a^{m cdot n}
$$

a)
$$
dfrac{4z^{-3}}{20z^{-1}}=dfrac{4}{20}z^{-3-(-1)}=dfrac{1}{5}z^{-3+1}=dfrac{1}{5}z^{-2}=dfrac{1}{5z^2}
$$

b)
$$
(2^3y^8)(3^2y^{-10})=8 cdot 9 cdot y^{8+(-10)}=72y^{8-10}=72y^{-2}=dfrac{72}{y^2}
$$

c)
$$
(6g^3)^{-3}=6^{-3}g^{3 cdot (-3)}=dfrac{1}{6^3} cdot g^{-9}=dfrac{1}{216} cdot g^{-9}=dfrac{1}{216g^9}
$$

The relationship between $Delta PQR$ and $Delta P’Q’R’$ is that the perpendicular distance between all the points between the original triangle and the exact points in its reflection is equal from the line of reflection. For example Distance of point Q and Q’ is same and is equal to $sqrt 5$ from the line $l$.

The relationship between $Delta PQR$ and $Delta P’Q’R’$ is that the perpendicular distance between all the points between the original triangle and the exact points in its reflection is equal from the line of reflection.

$textbf{(a)}$ The relationship between $y=dfrac{3}{5}-4$ and its image is that the image is translated above by 5 units of distance. The slope of both the lines are the same. The difference between them is that they have different $y$-intercepts

$textbf{(b)}$ The relationship between the line and its image is that they are perpendicular to each other and perpendicular distance on the both from the origin is the same.

$textbf{(c)}$ The slope of the given line is $dfrac{3}{5}$ and slope of its reflection is $-dfrac{5}{3}$. There product of slope is equal to $-1$, which is a mathematical way of saying that these are perpendicular to each other.

$textbf{(a)}$ The equation of the resultant line is $y=dfrac{3}{5}+1$. For graph see inside.

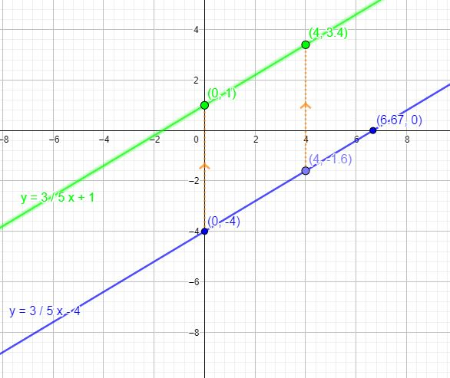
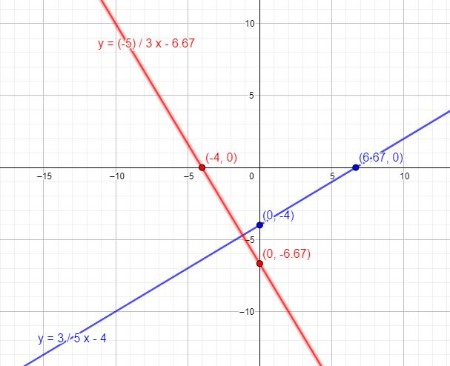
$textbf{(b)}$ The equation of the resultant line is $y=-dfrac{5}{3}-6.67$.For graph see inside.

$textbf{(c)}$ The slope of the given line is $dfrac{3}{5}$ and slope of its reflection is $-dfrac{5}{3}$. There product of slope is equal to $-1$, which is a mathematical way of saying that these are perpendicular to each other.

$text{color{#c34632}(a)}$ When the line rotates that means the slope triangle will also rotates, So the $Delta y$ and the $Delta x$ will replace each other and that means they will switch places in the fraction of the slope form $color{#4257b2} m= dfrac{ Delta y}{ Delta x}$.

And as shown in the given gragh the original line has a positive direction slope and after rotation the rotated line has a negative direction slope.

So from the mentioned reasons, We can estimate that if the original line has a slope equals to $color{#4257b2} dfrac{a}{b}$ the perpendicular line must always have a slope equals $color{#c34632} – dfrac{b}{a}$ if neither $a$ nor $b$ is zero.

$text{color{#c34632}(b)}$ If the original line has a slope of $0$ that means the $Delta y = 0$ for that line and the $Delta x$ has a value after rotation $90 text{textdegree}$ the $Delta y$ and the $Delta x$ switch places in the fraction of the slope and that will make us divide by zero which give us undefined value. So the slope of the perpendicular line would have an undefined value, We can represent that perpendicular line by a vertical line.

a) Given: goes through the point (0,-3),
perpendicular to the line $y=-dfrac{2}{5}x+6$

That means the slope is equal to $m=dfrac{5}{2}$,
because in perpendicular lines $m_1 cdot m_2=-1$ and $m_1=-dfrac{2}{5}$

Using formula $y-y_1=m(x-x_1)$ and
plugging in the given values $x_1=0, ; y_1=-3$

$$
y-(-3)=dfrac{5}{2}(x-0)
$$

$$
y+3=dfrac{5}{2}x
$$

$$
y=dfrac{5}{2}x-3
$$

b) Given: goes through the point (0,7),
perpendicular to the line $y=dfrac{3}{2}x+5$

That means the slope is equal to $m=dfrac{3}{2}$

because in parallel lines $m_1=m_2$ and $m_1=dfrac{3}{2},$

Using formula $y-y_1=m(x-x_1)$ and
plugging in the given values $x_1=0, ; y_1=7$

$$
y-7=dfrac{3}{2}(x-0)
$$

$$
y-7=dfrac{3}{2}x
$$

$$
y=dfrac{3}{2}x+7
$$

Equation of line A is given as $y=dfrac{6}{5}x-10$. The slope of this line is $dfrac{6}{5}$.

Any line parallel to this line will have same slope and any line perpendicular to this line will have a slope $-dfrac{5}{6}$ as product of the slope of two perpendicular lines are equal to $-1$.

Now, Given that line C is perpendicular to line A. Also, Line D is perpendicular to both line C and line E which means that line C and line E are parallel. As line C is perpendicular to line A this means line E is also perpendicular to line A which means it slope should be $-dfrac{5}{6}$

Line E is perpendicular to line A and has a slope $-dfrac{5}{6}$

Slopes of the perpendicular lines
The relationship between the slopes of the two perpendicular lines is that their product of the slope is $-1$. So when we are given the slope of a line, then the slope of its perpendicular line can be found out by dividing -1 by the slope of the given line, which is shown below.

Let the slope of a line is $m$, then the slope of its perpendicular line is given by

$$
text{Slope$bot$}=dfrac{-1}{m}
$$

Let the slope of a line is $m$, then the slope of its perpendicular line is given by

$$
text{Slope$bot$}=dfrac{-1}{m}
$$

For a given line with two points $(x_1,y_1)$ and $(x_2, y_2)$ on it, the slope $m$ of such line is defined by
$$
m=dfrac{y_2-y_1}{x_2-x_1}
$$
Given that the line with negative slope(going in downward direction) passes through points (0,4) and point of intersection of both the lines which is (2,1) which can be seen from the given graph.

Hence, slope of this line is $m_1= dfrac{1-4}{2-0}= -dfrac{3}{2}$

Further, evaluating the slope of second line, as it passes through points (0,0) and point of intersection of both lines which is (2,1).

Slope of this line is $m_2= dfrac{1-0}{2-0}=dfrac{1}{2}$

As, we know that product of the slope the two perpendicular lines should be $-1$, but in this case it is $m_1times m_2=-dfrac{3}{2}times dfrac{1}{2}=-dfrac{3}{4}$.
Hence, Mario is correct and these two lines are $textbf{not perpendicular}$

Using:

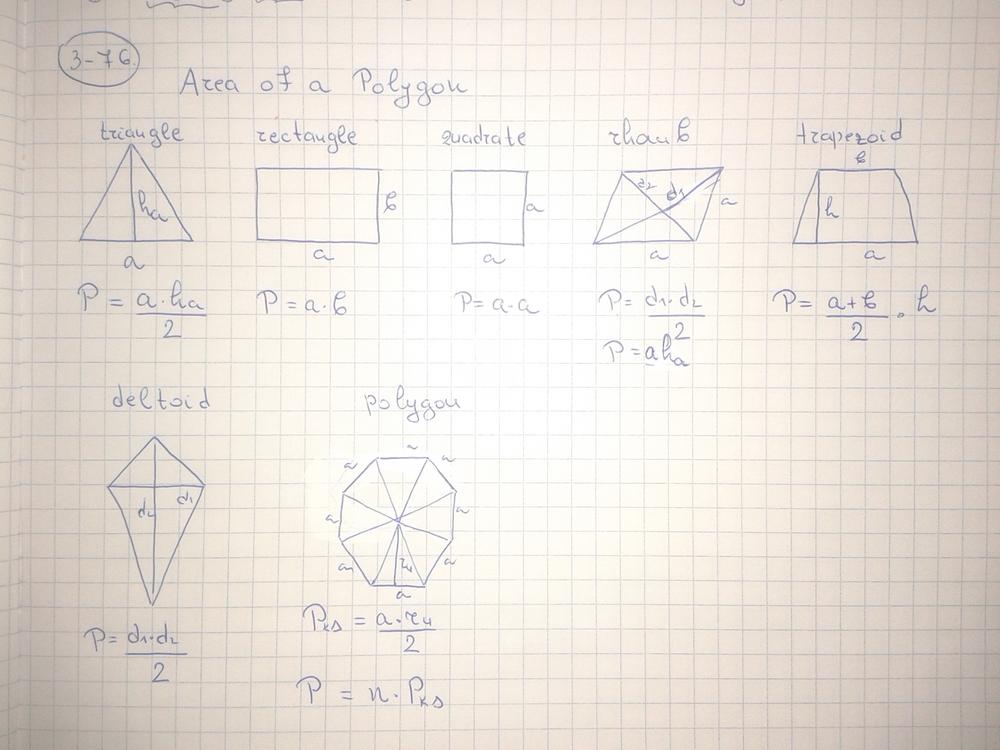
Formula for perimeter of a rectangle $P=2a+2b$

Formula for area of a rectangle $A=a cdot b$

a)
$$
a=2x
$$

$$
b=x+3
$$

$$
P=2 cdot 2x+2(x+3)=4x+2x+6=6x+6
$$

b)
$$
P=78
$$

$$
78=6x+6
$$

$$
78=6(x+1)
$$

$$
x+1=13
$$

$$
x=12
$$

So, $a=2x=2cdot 12=24$ cm

$b=x+3=12+3=15$ cm

c) Verify $A=360 ; cm^2$

$$
A=a cdot b
$$

$$
360=24 cdot 15
$$

$$
360=360
$$

Yes, the area is equal to $360 ; cm^2$

Figure 1 has 11 tiles and from the graph it can be seen that figure 3 has 7 tiles. Assuming the linear relations, we can represent the situation as two points $(1,11)$ and $(3,7)$ on a line for which we need equation. Now, that we have two points on the line, we can find the equation by using the method shown below.

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Now, we have given points as $(1,11)$ and $(3,7)$. Let $(x_1,y_1)=(1,11)$ and $(x_2,y_2)=(3,7)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{7-11}{3-1}\
&=dfrac{-4}{2}\
&=-2
end{align*}
$$

Now, the equation of a line of slope $-2$ passing through a point $(1,11)$ is given by

$$
begin{align*}
y-(11)&=-2cdot (x-1)\
y-11&=-2cdot x + -2cdot(-1) \
y&=-2cdot x + 2+11 \
y&=-2cdot x +13 \
end{align*}
$$

$$
y=-2cdot x +13
$$

Is the question about the mass (in kilograms) or the wingspan (in meters)?

This is about the mass (in kilograms).
So set up a ratio of the mass of the flying fox to the bumblebee bat.

Answer is:

$$
dfrac{1.6 kilograms}{2 times 10^{-3} kilograms}= 800
$$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{29}{9}+frac{79}{9}\\
& =frac{-29+79}{9} \
&=frac{50}{9}tag{Add/Subtract the numbers} \\
&=boxed{{color{#c34632} 5frac{5}{9} } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Apply:rule}:frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{51}{7}-frac{21}{5}\\
& =-frac{51cdot :5}{35}-frac{21cdot :7}{35} tag{Adjust fraction} \
&=frac{-51cdot :5-21cdot :7}{35}\
&=frac{-402}{35} \
&=-frac{402}{35}\\
&=boxed{{color{#c34632} -11frac{17}{35} } }
end{align*}
$$

$$
color{#c34632}text{}mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=frac{12}{7}cdot frac{27}{7}\\
& =frac{12cdot :27}{7cdot :7} tag{Multiply fraction} \
&=frac{12cdot :27}{49} tag{Multiply the numbers}\
&=frac{324}{49}tag{Multiply the numbers}\\
&=boxed{{color{#c34632} 6frac{30}{49} } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Multiply:fractions}:quad frac{a}{b}cdot frac{c}{d}=frac{a:cdot :c}{b:cdot :d}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=-frac{57}{7}div :-frac{50}{9}\\
& =-frac{frac{57}{7}}{frac{50}{9}} \
&=-frac{57cdot :9}{7cdot :50} tag{Divide fractions}\
&=-frac{57cdot :9}{350}tag{Multiply the numbers}\
&=-left(-frac{513}{350}right)tag{Multiply the numbers}\
&= frac{513}{350} \
&=boxed{{color{#c34632} 1frac{163}{350}} }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Apply:the:fraction:rule}:quad frac{a}{-b}=-frac{a}{b}
$$

$$
color{#c34632} text{}mathrm{Divide:fractions}:quad frac{frac{a}{b}}{frac{c}{d}}=frac{acdot :d}{bcdot :c}
$$

$$
color{#c34632} text{}mathrm{Apply:rule}:-left(-aright)=a
$$

$$
text{}
$$

$$
color{#4257b2} text{a)} 5frac{5}{9}
$$

$$
color{#4257b2} text{b)} -11frac{17}{35}
$$

$$
color{#4257b2} text{c)}6frac{30}{49}
$$

$$
color{#4257b2} text{d)}1frac{163}{350}
$$

$textbf{(a)}$ Shape of the given figure will not change for given rotation by either of 45$text{textdegree}$, 90$text{textdegree}$ or 180 $text{textdegree}$.

$textbf{(b)}$ For the rotation of 360$text{textdegree}$, the shape of any figure will not change and so for the given figure also it will not change.

$textbf{(c)}$ A circle’s shape will not change for any possible rotation by any angle for rotation about its center.

$textbf{(a)}$ Shape of the given figure will not change for given rotation by either of 45$text{textdegree}$, 90$text{textdegree}$ or 180 $text{textdegree}$.

$textbf{(b)}$ For the rotation of 360$text{textdegree}$, the shape of any figure will not change and so for the given figure also it will not change.

$textbf{(c)}$ A circle’s shape will not change for any possible rotation by any angle for rotation about its center.

$bullet$ Yes, it does make difference if the rotation is clockwise versus counterclockwise. It matters in the situation when the rotation is by any other angle other than 180 $text{textdegree}$ or 360$text{textdegree}$.

$bullet$ For rotation by $360text{textdegree}$ it doesn’t matter

$bullet$ For the rotation by 360 $text{textdegree}$ the image lies exactly on the original shape.

$textbf{(a)}$ The relationship between segment PP’, QQ’ and RR’ is that these are parallel to each other. This is because All the segment PP’, QQ’ and RR’ are perpendicular to the line of reflection, hence these are parallel to each other.

We can algebraically verify this observation by finding slope of each segment separately and if these all have the same value of slope then these are parallel to each other.
Now, for finding the slope of each segment, we need to find the two points on the segment, The respective points are shown in the graph attached below.

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

$bullet$ Calculating the slope for segment PP’.

The points on the segment PP’ are $(2.5,3.5)$ and $(4.5,2.5)$

$Rightarrow$
$$
text{slope}=dfrac{2.5-3.5}{4.5-2.5}=dfrac{-1}{2}=-dfrac{1}{2}
$$

$bullet$ Calculating the slope for segment QQ’.

The points on the segment QQ’ are $(1,3)$ and $(5,1)$

$Rightarrow$
$$
text{slope}=dfrac{1-3}{5-1}=dfrac{-2}{4}=-dfrac{1}{2}
$$

$bullet$ Calculating the slope for segment RR’.

The points on the segment QQ’ are $(0,1)$ and $(4,-1)$

$Rightarrow$
$$
text{slope}=dfrac{-1-1}{4-0}=dfrac{-2}{4}=-dfrac{1}{2}
$$

We can see that the slope of the each segment is the same and hence it is verified that these segments are parallel to each other.

$textbf{(a)}$ The graph of the given figure is attached below.

$textbf{(b)}$ The relationship between the segment RR’ and the line of reflection is that these are perpendicular to each other. This can be explained using the property of the reflection across a line, which is the line of reflection here.

$textbf{(c)}$ For proving algebraically that the segment RR’ and line of reflection is perpendicular to each other, we can show that the product of the their slope is $-1$.

We have calculated the slope of the segment RR’ as $-dfrac{1}{2}$ in the part (a). Now, we need to find the slope of the line of reflection as explained above.
The two points on the line of reflection are $(2,0)$ and $(3,2)$

$Rightarrow$
$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

$$
text{slope}=dfrac{2-0}{3-2}=2
$$

The product of their slope is $-dfrac{1}{2}times 2=-1$, hence, result is verified algebraically.

$textbf{(d)}$ The distance of both the segment RN and NR’ is the same. We can evaluate the length using the pythagoras theorem and the information from the graph below.

$$
text{Length of RN }= sqrt{2^2+1^2}=sqrt{5}
$$

$$
text{Length of NR’ }= sqrt{2^2+1^2}=sqrt{5}
$$

$textbf{(e)}$ Yes, the line segment connecting a point to its image is always perpendicular to the line of reflection and the line of reflection is always at the midpoint of this segment. Using the results of the rigid transformation, we know that the reflection preserve the shape and size of the object. The distance between the object and its image is equal from the line of reflection and any line joining a point on the object and its image is perpendicular to the line of reflection.

$textbf{(a)}$ All the line segment are parallel with each other and have the same slope which is equal to $-dfrac{1}{2}$

$textbf{(b)}$ The relationship between the segment RR’ and the line of reflection is that these are perpendicular to each other.

$textbf{(c)}$ The product of their slope is $-dfrac{1}{2}times 2=-1$.

$textbf{(d)}$ The distance of both the segment RN and NR’ is the same.

$textbf{(e)}$ Yes, the line segment connecting a point to its image is always perpendicular to the line of reflection and the line of reflection is always at the midpoint of this segment.

The given equation of line of reflection is $y=-dfrac{2}{5}+6$. As we know that the line joining the a point and its reflection is always perpendicular to the line of reflection. So, in order to verify the answer of Evan, We need to find the slope of the line containing the points $(5,7)$ and $(2,2)$. If the product of the slope of this line with the slope of the line of reflection is $-1$ then these line are perpendicular and point $(2,2)$ can be the reflection of the point $(5,7)$ if their distance from the line $y=-dfrac{2}{5}+6$ is the same.

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

we have given points as $(5,7)$ and $(2,2)$. Let $(x_1,y_1)=((5,7))$ and $(x_2,y_2)=(2,2)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{2-7}{2-5}\
&=dfrac{-5}{-3}\
&=dfrac{5}{3}
end{align*}
$$

Now, we find the product of the slopes of the both the lines

$$
begin{align*}
text{product}&=text{Slope of line of reflection}times text{Slope by points}\
&=-dfrac{2}{5}times dfrac{5}{3}\
&=-dfrac{2}{3}
end{align*}
$$

As we can see , it fails even the first requirement to be the reflection point, as the product of the slope of line through points $(5,7)$ and $(2,2)$ with the slope of the line of reflection is not equal to $-1$. Hence, Evan cannot be correct.

Points fails even the first requirement to be the reflection point, as the product of the slope of line through points $(5,7)$ and $(2,2)$ with the slope of the line of reflection is not equal to $-1$. Hence, Evan cannot be correct.

$textbf{(a)}$For finding how many units to the right and how many units down did the translation move the triangle, we can select any one point on the given figure and same point on the translated figure. As every point on the shape undergoes same translation, then by finding translation of this single point we can tell about the translation of the whole figure.

Now, lets choose the point as C$(-1,4)$ and its translated image C’$(6,1)$

$bullet$ Finding the right shift, we need to take the difference of the $x$ coordinates, which is

$$
text{Right shift}=text{Final $x$ coordinate}-text{Initial $x$ coordinate}
$$

$$
text{Right shift}=6-(-1)=7text{ Units}
$$

$bullet$ Finding the downward shift, we need to take the difference of the $y$ coordinates, which is

$$
text{Downward shift}=text{Final $y$ coordinate}-text{Initial $y$ coordinate}
$$

$$
text{Downward shift}=1-4=-3 text{ Units}
$$

Therefore, the $Delta ABC$ is translated right by 7 units and translated downward by 3 units as negative sign shows here the downward movement as we calculated difference of final coordinates and initial coordinates.

$textbf{(b)}$ We need to perform a translation of 7 units in right direction and 3 units in downward direction. Figure is attached below.

$textbf{(c)}$ The segments joining the vertex points are parallel to each other. This tells that each and every point on the shape is translated with the same translation and preserves the exact shape of the figure.Figure is attached below.

$textbf{(d)}$ Using tracing paper we can cut the shape to fit the $Delta EFG$ then we see that it fits exactly the translated image $Delta E’F’G’$. This shows that translation preserves the angles and the lengths of a figure.

$textbf{(a)}$ $Delta ABC$ is translated right by 7 units and translated downward by 3 units

$textbf{(b)}$ We need to perform a translation of 7 units in right direction and 3 units in downward direction. See the Figure inside.

$textbf{(c)}$ The segments joining the vertex points are parallel to each other. This tells that each and every point on the shape is translated with the same translation and preserves the exact shape of the figure.See the Figure inside.

$textbf{(d)}$ Using tracing paper we can cut the shape to fit the $Delta EFG$ then we see that it fits exactly the translated image $Delta E’F’G’$. This shows that translation preserves the angles and the lengths of a figure.

$textbf{(b)}$ The transformation used to obtain $Delta$A’B’C’ from $Delta$ABC is reflection about the line $y=-x$

$textbf{(c)}$ The function (x, y)$rightarrow$(x- 6, y – 3) will give the resultant points for the $Delta$A”B”C” as shown below.

Point A$(3,3)$ $rightarrow$ Point A”$(-3,0)$

Point B$(1,1)$ $rightarrow$ Point B”$(-5,-2)$

Point C$(6,1)$ $rightarrow$ Point C”$(0,-2)$

The transformation used here is the translation of $Delta$ABC to 6 unit leftward and 3 units downwards.

$textbf{(d)}$ Figure attached below.

$textbf{(e)}$ Reflection about line $y=-x$ mapped the quadrilateral WXYZ to its image.

$textbf{(a)}$ For figure see inside.

$textbf{(b)}$ The transformation used to obtain $Delta$A’B’C’ from $Delta$ABC is reflection about the line $y=-x$

$textbf{(c)}$ The transformation used here is the translation of $Delta$ABC to 6 unit leftward and 3 units downwards.

$textbf{(d)}$ For figure see inside.

$textbf{(e)}$ Reflection about line $y=-x$ mapped the quadrilateral WXYZ to its image.

$textbf{(a)}$ The special polygon formed by joining A , B ans A’ is a triangle.

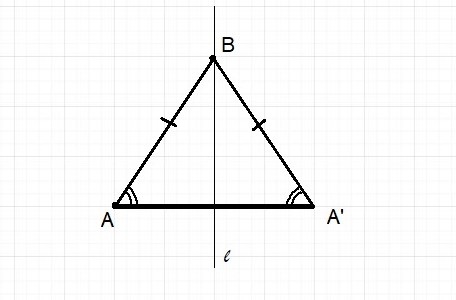
$textbf{(b)}$ As the side BA’ is the reflection of side BA hence there length is same, this implies the $angle BAA’ = angle BA’A$ and hence the special thing about this triangle is that it’s an Isosceles triangle.

$textbf{(a)}$ Triangle

$textbf{(b)}$ Isosceles triangle

To rotate any object $90text{textdegree}$ clockwise about the origin that means the coordinates of any point of it convert from

$color{#c34632} (x, y) Rightarrow (y, -x)$

$A(-3, 4) Rightarrow A'(4, 3)$

$B(1, 6) Rightarrow B'(6, -1)$

$C(5, -2) Rightarrow C'(-2, -5)$

$D(1, -4) Rightarrow D'(-4, -1)$

We plot the points A, B, C and D and their image A’, B’,C’ and D’ as shown in gragh.

$A'(4, 3)$

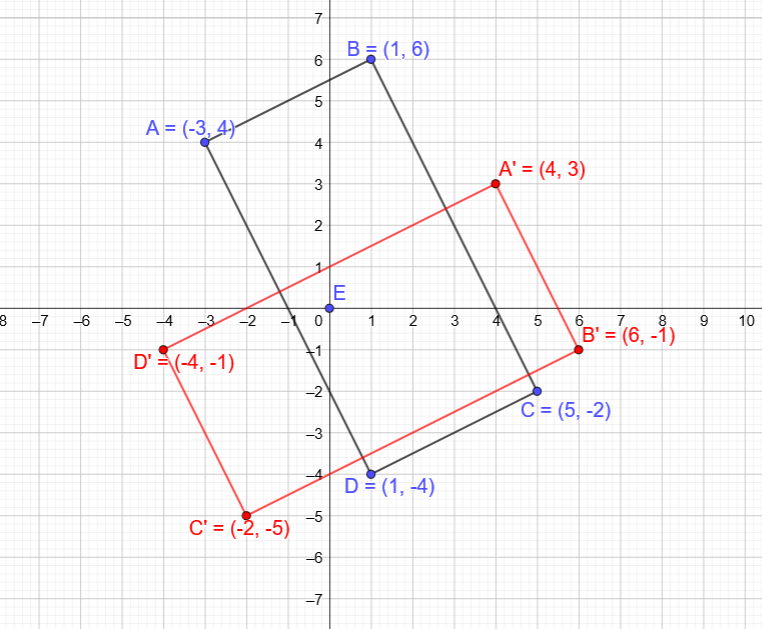
$B'(6, -1)$

$C'(-2, -5)$

$D'(-4, -1)$

A rigid transformation always preserves the shape and size of the figure. $Delta$HGJ is not the rigid transformation of the $Delta$HGJ because their side length are not the same. However, the shape is preserved as both are the right angled triangles with similar respective sides.

Side AB $rightarrow$ Side HG

Side BC $rightarrow$ Side GJ

Side CA $rightarrow$ Side JH

A rigid transformation always preserves the shape and size of the figure. $Delta$HGJ is not the rigid transformation of the $Delta$HGJ because their side length are not the same.

Given info:

Perimeter=52 units

$a=19$

$b=7x-4$

$$
c=10x+3
$$

Using formula for perimeter of a triangle $P=a+b+c$

$$
52=19+7x-4+10x+3
$$

$$
52=18+17x
$$

$$
17x=34
$$

$$
x=2
$$

So, $a=19, ; b=7 cdot 2-4=14-4=10, ; c=10 cdot 2+3=23$

$textbf{(a)}$ Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Now, we have given points as $(-7,10)$ and $(1,4)$. Let $(x_1,y_1)=(-7,10)$ and $(x_2,y_2)=(1,4)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{4-10}{1-(-7)}\
&=dfrac{-6}{8}\
&=-dfrac{3}{4}
end{align*}
$$

Now, the equation of a line of slope $-dfrac{3}{4}$ passing through a point $(1,4)$ is given by

$$
begin{align*}
y-(4)&=-dfrac{3}{4}cdot (x-1)\
y-4&=-dfrac{3}{4}cdot x -dfrac{3}{4}cdot (-1)\
y&=-dfrac{3}{4}cdot x +dfrac{3}{4} +4\
y&=-dfrac{3}{4}cdot x +dfrac{3+16}{4}\
y&=-dfrac{3}{4}cdot x +dfrac{19}{4}\
end{align*}
$$

$$
textbf{(b)}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Now, the equation of a line of slope $-dfrac{3}{4}$ passing through a point $(-14,4)$ is given by

$$
begin{align*}
y-(4)&=-dfrac{3}{4}cdot (x-(-14))\
y-4&=-dfrac{3}{4}cdot x -dfrac{3}{4}cdot (+14)\
y-4&=-dfrac{3}{4}cdot x +dfrac{42}{4} \
y&=-dfrac{3}{4}cdot x +dfrac{21}{2}+4\
y&=-dfrac{3}{4}cdot x +dfrac{21+8}{2}\
y&=-dfrac{3}{4}cdot x +dfrac{29}{2}\
end{align*}
$$

$$
textbf{(c)}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Now, the equation of a line of slope $0$ passing through a point $(6,-11)$ is given by

$$
begin{align*}
y-(-11)&=0cdot (x-6)\
y+11&=0\
y&=-11\
end{align*}
$$

$textbf{(a)}$ $y=-dfrac{3}{4}cdot x +dfrac{19}{4}$

$textbf{(b)}$ $y=-dfrac{3}{4}cdot x +dfrac{29}{2}$

$textbf{(c)}$ $y=-11$

Given function
$f(x)=sqrt{3x-2}$

Now plugging in values into the given function:

a)
$f(1)=sqrt{3 cdot 1-2}=sqrt{3-2}=sqrt{1}=1$

b) $f(9)=sqrt{3 cdot 9-2}=sqrt{27-2}=sqrt{25}=5$

c) $f(4)=sqrt{3 cdot 4-2}=sqrt{12-2}=sqrt{10}$

d) $f(0)=sqrt{3 cdot 0-2}=sqrt{0-2}=sqrt{-2}$

Using Complex Numbers $i^2=-1$

$$
sqrt{-2}=sqrt{-1 cdot 2}=sqrt{i^2 cdot 2}=isqrt{2}
$$

$textbf{(a)}$
$$
begin{align*}
dfrac{x}{8}&=dfrac{3}{4} tag{multiply each side by 8}\
dfrac{x}{8}cdot 8&=dfrac{3}{4}cdot 8 \
(dfrac{8}{8})cdot x&=dfrac{3cdot 8 }{4}\
x&=6cdot (dfrac{4}{4})\
x&=6
end{align*}
$$

$textbf{(b)}$
$$
begin{align*}
5x – (x + 1) &= 5 – 2x tag{collect like terms each side}\
(5x-x)-1&=5-2x \
4x-1&=5-2x tag{add 2x to each side}\
4x+2x-1&=5-2x+2x\
6x-1&=5 tag{add +1 to each side}
6x-1+1&=5+1\
6x&=6 tag{divide each side by 6}\
dfrac{6}{6}x&=dfrac{6}{6}\
x&=1
end{align*}
$$

$textbf{(c)}$
$$
begin{align*}
3x +5 -x &=x-3 tag{collect like terms each side}\
(3x-x)+5&=x-3 \
2x+5&=x-3 tag{subtract x from each side}\
2x-x+5&=x-x-3\
x+5-5&=-3-5 tag{add -5 to each side}\
x&=-8\
end{align*}
$$

$textbf{(d)}$
$$
begin{align*}
dfrac{2}{5}&=dfrac{x}{40} tag{multiply each side by 40}\
dfrac{2}{5}cdot 40&=dfrac{x}{40}cdot 40\
(dfrac{40}{5})cdot 2&=dfrac{40}{40}cdot x\
8cdot 2 &=x tag{Interchange sides}\
x&=16
end{align*}
$$

$textbf{(a)}$ 6

$textbf{(b)}$ 1

$textbf{(c)}$ -8

$textbf{(d)}$ 16

The reflection of a half square is depicted below. All the dotted lines are the lines of reflection , half square is drawn in solid black and the red lines are the reflections across the respective lines which are marked as $l, m, n$ and $j$

$textbf{(b)}$ Solid black is the original half square and red half square is the result of the rotation with center as the point of rotation.

$textbf{(c)}$ Repeating the process, for the right angled triangle, Solid black is the original figure, and dotted lines are the line of reflections and green figures are the reflected images.

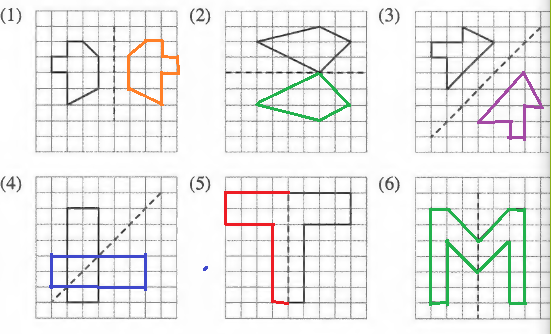
All the reflections for the other figures can be derived like this only. Repeating all the figures will make the answer too long. I hope the idea is clear here.

$textbf{(c)}$ Solid black is the original triangle and red lines is the result of the rotation with the shown center as the point of rotation.

In order to locate the fourth point of the rectangle, two things we need to keep in the mind is that all the sides should make the 90$text{textdegree}$ with each other and the length of the parallel sides should be same. When we start locating the given point, considering the above mentioned points, it will be easy to locate the fourth point. All the graphs are attached below, The points in the red colour show the unknown points.

$textbf{(a)}$ Calculating the area

Side length $=9-(-1)=10$ units

Side breadth $=3-2=1$ unit

Area of Rectangle $=$ Length$times$breadth

$Rightarrow$ Area$=10times 1=10 text{ unit}^2$

$textbf{(b)}$ Calculating the area

Side length $=7-(-3)=10$ units

Side breadth $=5-3=2$ unit

Area of Rectangle $=$ Length$times$breadth

$Rightarrow$ Area$=10times 2=20 text{ unit}^2$

$textbf{(c)}$ Calculating the area

Side length $=sqrt{9^2+6^2}=10.82$ units

Side breadth $=sqrt{3^2+2^2}=3.61$ unit

Area of Rectangle $=$ Length$times$breadth

$Rightarrow$ Area$=10.82times 3.61=39.06 text{ unit}^2$

$textbf{(d)}$ Calculating the area

Side length $=1483-(73)=1410$ units and Side breadth $=96-(-52)=148$ unit

Area of Rectangle $=$ Length$times$breadth

$Rightarrow$ Area$=1410times 148=208680 text{ unit}^2$

$textbf{(a)}$ Area$=10 text{ unit}^2$

$textbf{(b)}$ Area$=20 text{ unit}^2$

$textbf{(c)}$ Area$=39.06 text{ unit}^2$

$textbf{(d)}$ Area$=208680 text{ unit}^2$

The lines (a) and (b) are perpendicular because multiple slopes is $dfrac{1}{3}cdot (-3)=-1$

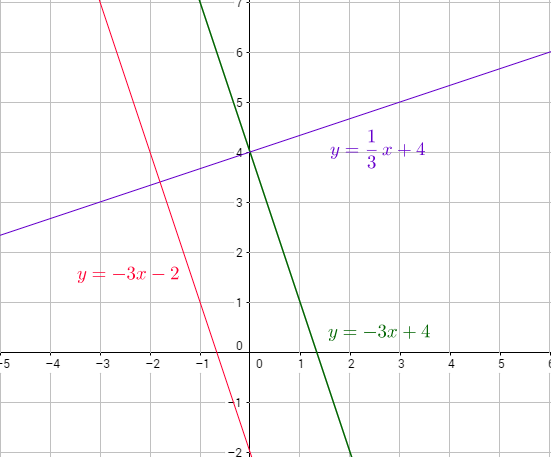
The lines (b) and (c) are parallel because they have same slopes -3

$textbf{(a)}$ Given equation is $dfrac{x}{6}=dfrac{5}{2}$ . In order to get $x$ alone, we need to multiply the both side by 6.

$textbf{(b)}$
$$
begin{align*}
dfrac{x}{6}&=dfrac{5}{2} tag{multiply both side by 6}\
dfrac{x}{6}cdot 6&=dfrac{5}{2} cdot 6\
dfrac{6}{6}cdot x&=dfrac{6}{2}cdot 5\
1cdot x&=3cdot 5\
x&=15
end{align*}
$$

$textbf{(c)}$
$$
begin{align*}
dfrac{x}{10}&=dfrac{2}{5} tag{multiply both side by 10}\
dfrac{x}{10}cdot 10&=dfrac{2}{5} cdot 10\
dfrac{10}{10}cdot x&=dfrac{10}{5}cdot 2\
1cdot x&=2cdot 2\
x&=4
end{align*}
$$

$textbf{(a)}$ In order to get the $x$ alone, we need to multiply both side by 6

$textbf{(b)}$ 15

$textbf{(c)}$ 4

In simple words, we can say that a number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10.

In order to write any given number into the scientific notation, we need to follow some sets of rules.

The number should be written in such a way that there should be a decimal point immediately after the leftmost digit, which should be greater than 1 and less than 10. After this decimal points required number of digits are put and then multiplication by a power of 10 with the sign of multiplication as it is.
For example $2.566times 10^-9$ is written in scientific form.

$textbf{(a)}$ Given number is 370,000,000

The correct scientific notation representation of this number is $3.7times 10^8$

$textbf{(b)}$ Given number is 7600

The correct scientific notation representation of this number is $7.6times 10^3$

$textbf{(a)}$ $3.7times 10^8$

$textbf{(b)}$ $7.6times 10^3$

Given that, Chi can read 40 pages in 3 minutes. So, time required by him to read a single page is equal to $dfrac{3}{40}$ minutes.

Now, to read a 265 page novel , the times required is

$$
text{Total time}=text{time taken to read one page}times text{number of pages to read}
$$

$$
text{Total time}=dfrac{3}{40} times 265= 19.87 text { minutes}
$$

$textbf{(a)}$ Hexagon does not change its shape, although its side AB get shifted to A’B’.

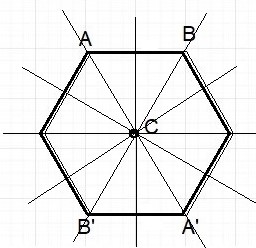
$textbf{(b)}$ hexagon’s shape remained the same when original polygon is reflected along the line $n$.

$textbf{(c)}$ Yes, regular hexagon have many other lines of symmetry , which is shown in the structure above.

$textbf{(a)}$ Shape remains same.

$textbf{(b)}$ Shape remains same.

$textbf{(c)}$ Yes, it has many other lines of symmetry.

$text{color{#c34632}(a)}$ The shapes have reflection symmetry are regular hexagon, kite, rectangle, square, circle, equilateral triangle, isosceles right triangle, rhombus, isosceles triangle, isosceles trapezoid, regular pentagon.

The reflection symmetry means that the shape can be cut into two equal parts as shown.

$text{color{#c34632}(b)}$ Equilateral triangle, isosceles right triangle and isosceles triangle are the types of triangles have reflection symmetry.

$text{color{#c34632}(c)}$ Kite, rectangle, square, rhombus and isosceles trapezoid are the types of quadrilaterals have reflection symmetry.

$text{color{#c34632}(d)}$ Regular hexagon, square, circle and regular pentagon are the shapes which have more than three lines of symmetry.

$textbf{(a)}$ Yes, the given diagram is a polygon. A polygon is a 2D closed shape made of straight lines.

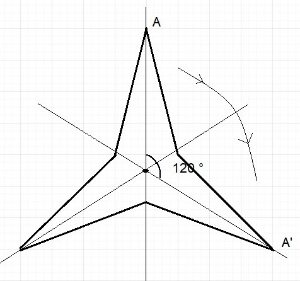
$textbf{(b)}$ Yes, the can be rotated on itself for every rotation of 120$text{textdegree}$. The point of rotation is the centre of the polygon.

$textbf{(c)}$ Jessica is talking about rotating all the polygons by 360 $text{textdegree}$ . Doing this will not change the polygon at all.

$textbf{(d)}$ The regular polygons have the rotation symmetry like the square, equilateral triangle or the example figure given to us.
In the resource page from the given shapes of triangle equilateral triangle has the rotation symmetry.

$textbf{(e)}$ From quadrilaterals , Square has $90 text{textdegree}$ rotation symmetry.

$text{color{#c34632}(a)}$ No, there isn’t a polygon that can be translated so that its end result is exactly the
same as the original object.

Translation symmetry means that the shape can be shifted onto itself.

$text{color{#c34632}(b)}$ All lines can be translated so that the end result is exactly the same as the original, Also tessellation that extends infinitely in all directions can be translated so that the end result is exactly the same as the original one.

$textbf{(a)}$ All those reflections falls on itself which have the lines of reflection pasing through the opposite vertex points and the mid point of the opposite sides as shown in the figure below.

$textbf{(b)}$ For each rotation of 36$text{textdegree}$ the decagon falls on itself. Also, For all the integral multiple of 36$text{textdegree}$, rotation falls on itself. This is because of symmetry of sides, which subtend an angle of 36$text{textdegree}$ at the centre of decagon.

$textbf{(c)}$ No translation can carry the decagon onto itself. Because with translation there will always be the change of the coordinates and hence it is not possible to translate decagon onto itself unless we perform translation and reverse translation to attain the same coordinates.

$textbf{(a)}$ All those reflections falls on itself which have the lines of reflection pasing through the opposite vertex points and the mid point of the opposite sides

$textbf{(b)}$ For each rotation of 36$text{textdegree}$ the decagon falls on itself. Also, For all the integral multiple of 36$text{textdegree}$, rotation falls on itself.

$textbf{(c)}$ No translation can carry the decagon onto itself. Because with translation there will always be the change of the coordinates and hence it is not possible to translate decagon onto itself unless we perform translation and reverse translation to attain the same coordinates.

$text{color{#c34632}(a)}$There are more than one definition of symmetry, each one depends on its type.

Reflection symmetry: A shape can be cut into two equal parts.

Rotation symmetry : A shape can be turned onto itself ( excluding $360 text{textdegree}$).

Translation symmetry : A shape can be shifted onto itself.

$text{color{#c34632}(b)}$ If we are not sure if a figure has reflection symmetry, we can use tracing paper or a reflective tool to explore and check according to the mentioned definitions of symmetry.

$text{color{#c34632}(c)}$ The types of symmetry are reflection symmetry, rotation symmetry and translation symmetry.

From the given part of the gragh, we estimate the coordinates of given point $color{#4257b2}(3, 3), (7, 3), (1, 1)$ and $color{#4257b2} (5, 1)$

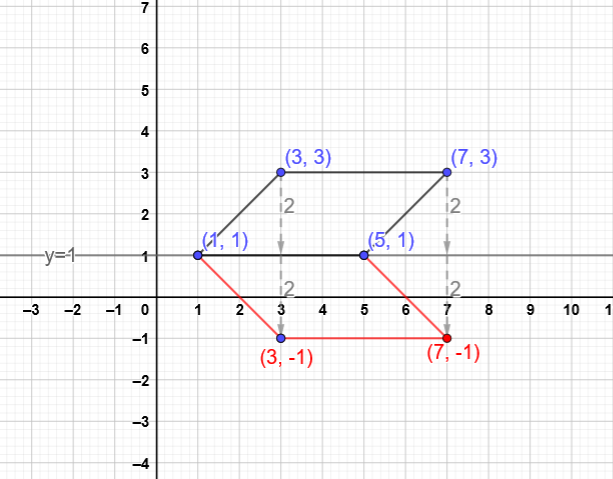
The line $color{#4257b2} y=1$ is the line of symmetry, So we need to reflect each given point around the line $y=1$ to get the second part of the gragh.

The two points $color{#4257b2} (1, 1)$ and $color{#4257b2} (5, 1)$ lie on the line of symmetry, So their projection are themselves (the image of each point is the same original point).

We find that the point $color{#4257b2}(3, 3)$ is about $2$ units from the line of symmetry, So we move from the line of symmetry also $2$ units to get its image. We get $color{#c34632}(3, -1)$ as shown in the gragh.

And so on the point $color{#4257b2} (7, 3)$, after moving $2$ units from the line of symmetry we get $color{#c34632}(7, -1)$ as shown.

As mentioned the missed vertices are $color{#c34632} (3, -1)$ and $color{#c34632} (7, -1)$.

The missed vertices are $(3, -1)$ and $(7, -1)$.

Given that square has sides of length $5x+2$ and its perimeter is 48.

$textbf{(a)}$ we know that the perimeter of square is 4 times the length of a side. So we can put it in the form of equation as shown below.

$$
48=4times(5x+2)
$$

$textbf{(b)}$ Solving the above equation for value of x

$$
begin{align*}
48&=4times(5x+2)\
dfrac{48}{4}&=5x+2\
5x&=12-2\
x&=dfrac{10}{5}\
x&=2
end{align*}
$$

$textbf{(c)}$ Area of square of side length $p$ is given by $p^2$. As we have x=2
$$
Rightarrow text{Side length of square}=5times 2 +2 =12 text{ units}
$$

$$
Rightarrowtext{area of square}=12times12=144 text{ units}
$$

$textbf{(a)}$ $48=4times(5x+2)$

$textbf{(b)}$ x=2

$textbf{(c)}$ 144 units

$textbf{(a)}$ The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

The equation of a line of slope $dfrac{4}{3}$ passing through a point $(0,-2)$ is given by

$$
begin{align*}
y-(-2)&=dfrac{4}{3}cdot (x-0)\
y+2&=dfrac{4}{3}cdot x\
y&=dfrac{4}{3}cdot x-2
end{align*}
$$

$textbf{(b)}$ The given transformation is translation. The property of the translation is that each and every point follows the same translation. So , the given point $(0,-2)$ will also follow the same translation, so coordinates of the final point after the translating this can be found out as

$x$ coordinate $rightarrow$ $0+3=3$

$y$ coordinate $rightarrow$ $-2+4=2$

Therefore, on translating point $(0,-2)$ it becomes $(3,2)$, due to translation the slope will not change as there is no rotation. This means we need to find the line with the slope $dfrac{4}{3}$ and passing through a point $(3,2)$

$$
begin{align*}
y-(2)&=dfrac{4}{3}cdot (x-3)\
y-2&=dfrac{4}{3}cdot x + dfrac{4}{3}cdot (-3)\
y-2&=dfrac{4}{3}cdot x-4\
y&=dfrac{4}{3}cdot x-4+2\
y&=dfrac{4}{3}cdot x-2
end{align*}
$$

Therefore, we obtain the same line, after performing these translation. Graph below explains it well.

$textbf{(c)}$ The given transformation is translation. The property of the translation is that each and every point follows the same translation. So , the given point $(0,-2)$ will also follow the same translation, so coordinates of the final point after the translating $(0,-2)$ downward by 5 units can be found out as

$x$ coordinate $rightarrow$ No change

$y$ coordinate $rightarrow$ $-2+-5=-7$

Therefore, on translating point $(0,-2)$ it becomes $(0,-7)$, due to translation the slope will not change as there is no rotation. This means we need to find the line with the slope $dfrac{4}{3}$ and passing through a point $(0,-7)$

$$
begin{align*}
y-(-7)&=dfrac{4}{3}cdot (x-0)\
y+7&=dfrac{4}{3}cdot x\
y&=dfrac{4}{3}cdot x-7
end{align*}
$$

$textbf{(d)}$ All the three lines are parallel to each other. In fact, the original line and the line obtained in the part $textbf{(b)}$ are the overlapping lines and hence the same.

$textbf{(e)}$ The perpendicular lines have the product of their slope equal to -1. therefore, a line perpendicular to these lines will have a slope of $dfrac{-1}{dfrac{4}{3}}=-dfrac{3}{4}$.
So, the equation of a line of slope $-dfrac{3}{4}$ passing through a point $(12,7)$ is given by

$$
begin{align*}
y-(7)&=-dfrac{3}{4}cdot (x-12)\
y-7&=-dfrac{3}{4}cdot x -dfrac{3}{4}cdot (-12)\
y-7&=-dfrac{3}{4}cdot x+9\
y&=-dfrac{3}{4}cdot x+9+7\
y&=-dfrac{3}{4}cdot x+16
end{align*}
$$

$textbf{(a)}$ $y=dfrac{4}{3}cdot x-2$

$textbf{(b)}$ $y=dfrac{4}{3}cdot x-2$

$textbf{(c)}$ $y=dfrac{4}{3}cdot x-7$

$textbf{(d)}$ All the three lines are parallel to each other. In fact, the original line and the line obtained in the part $textbf{(b)}$ are the overlapping lines and hence the same.

$textbf{(e)}$ $y=-dfrac{3}{4}cdot x+16$

For finding the equation of line using the points given in the table, we need to choose any two points from the table and the equation can be written as follows. First we need to find the slope of the line.

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Let choose the two points from the table as $(2,5)$ and $(3,8)$. Let $(x_1,y_1)=(2,5)$ and $(x_2,y_2)=(3,8)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{8-5}{3-2}\
&=dfrac{3}{1}\
&=3
end{align*}
$$

Now, the equation of a line of slope $3$ passing through a point $(2,5)$ is given by

$$
begin{align*}
y-5&=3cdot (x-2)\
y-5&=3cdot x + 3cdot (-2)\
y-5&=3cdot x -6\
y&=3cdot x -6+5\
y&=3cdot x -1\
y&=3x-1
end{align*}
$$

$$
y=3x-1
$$

$textbf{(a)}$ We can solve the given functions by plugging the input values and solving for the result.

$$
begin{align*}
f(x)&=7+|x|\
f(-5)&=7+|-5| \
f(-5)&=7+5 tag{using $ |pm a|=a$}\
f(-5)&=12
end{align*}
$$

$$
textbf{(b)}
$$

$$
begin{align*}
g(x)&=x^3-5\
g(4)&=4^3-5 \
g(4)&=64-5\
g(4)&=59
end{align*}
$$

$$
textbf{(c)}
$$

$$
begin{align*}
f(x)&=7+|x|\
f(0)&=7+|0| \
f(0)&=7+0 tag{using $ |0|=0$}\
f(0)&=7
end{align*}
$$

$$
textbf{(d)}
$$

$$
begin{align*}
f(x)&=7+|2|\
f(2)&=7+2 \
f(2)&=7+2 tag{using $ |pm a|=a$}\
f(2)&=9
end{align*}
$$

$$
textbf{(e)}
$$

$$
begin{align*}
g(x)&=x^3-5\
g(-2)&=(-2)^3-5 \
g(-2)&=-8-5\
g(-2)&=-13
end{align*}
$$

$$
textbf{(f)}
$$

$$
begin{align*}
g(x)&=x^3-5\
g(0)&=0^3-5 \
g(0)&=0-5\
g(-2)&=-5
end{align*}
$$

$textbf{(a)}$ 12

$textbf{(b)}$ 59

$textbf{(c)}$ 7

$textbf{(d)}$ 9

$textbf{(e)}$ -13

$textbf{(f)}$ -5

$textbf{(b)}$
$$
begin{align*}
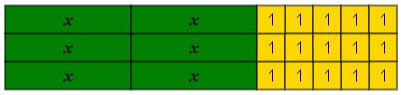
text{Total area}&=x^2+x+x+x+x+x+x+1+1+1+1+1+1+1+1\
&=x^2+6times x +8times 1\
&=x^2+6x +8 text{ Square units}
end{align*}
$$

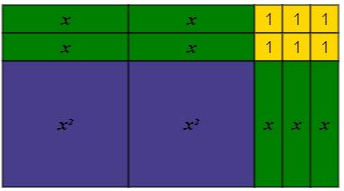
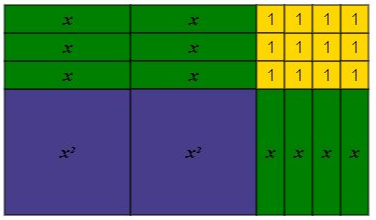
$textbf{(c)}$ From the figure, we can see that the length is $x+4$ units and the width is $x+2$ units.

$$
begin{align*}
text{Total Area}&=text{Length}times text{width}\
&=(x+4)times (x+2)
end{align*}
$$

$textbf{(d)}$
$$
x^2+6x +8=(x+4)times (x+2)
$$

$textbf{(b)}$ $x^2+6x +8$

$textbf{(c)}$ $(x+4)times (x+2)$

$$
textbf{(d)}x^2+6x +8=(x+4)times (x+2)
$$

#### a.

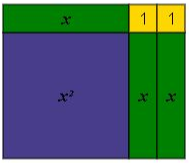
The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $x + 2$ for the length and $x + 1$ for the width.

$$
x^{2} + 3x + 1 = left ( x + 2right) left(x + 1right)
$$

#### b.

The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $2x + 5$ for the length and 2 for the width.

$$
6x + 15 = 3 left ( 2x + 5right)
$$

#### c.

The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $2x + 3$ for the length and $x + 2$ for the width.

$$
2x^{2} + 7x + 6 = left ( 2x + 3 right) left(x + 2 right)
$$

#### d.

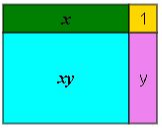
The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $x + 1$ for the length and $y + 1$ for the width.

$$
xy + x + y + 1 = left ( x + 1 right) left ( y + 1 right)
$$

#### e.

The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $2x + 4$ for the length and $x + 3$ for the width.

$$
2x^{2} + 10x + 12 = left ( 2x + 4 right) left ( x + 3 right)
$$

#### f.

The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $2y$ for the length and $y + 3$ for the width.

$$
2y^{2} + 6y = 2y left ( y + 3 right)
$$

#### g.

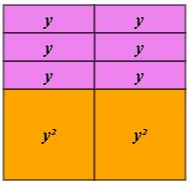
The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $y + x$ for the length and $y + 2$ for the width.

$$
y^{2} + xy + 2x + 2y = left ( y + x right) left ( y + 2 right)
$$

#### h.

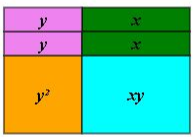
The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $3x + 1$ for the length and $x + 1$ for the width.

$$
3x^{2} + 4x + 1 = left ( 3x + 1 right) left ( x + 1 right)
$$

#### j.

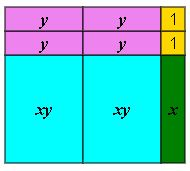
The given expression may be built as a rectangle using the different tiles. The rectangle has dimensions of $2y + 1$ for the length and $x + 2$ for the width.

$$
2xy + 4y + x + 2 = left ( 2y + 1 right) left ( x + 2 right)
$$

a. $left (x + 2right) left (x + 1right)$

b. $3 left(2x + 5right)$

c. $left(2x + 3right) left(x + 2right)$

d. $left(x + 1right) left(y + 1right)$

e. $left(2x + 4 right) left(x + 3 right)$

f. $2y left(y + 3 right)$

g. $left(y + x right) left(y + 2right)$

h. $left(3x + 1 right) left(x + 1 right)$

i. cannot be factored out

j. $left(2y + 1 right) left(x + 2right)$

Perimeter of any figure is given by the sum of the length of its all outer sides.

$textbf{(a)}$
$$
begin{align*}
text{Perimeter$_a$}&= (x+1+y+1+x)+(1)+(x+1+y+1+x)+(1)\
&=2(x+1+y+1+x)+2(1)\
&=2(2x+y+2)+2\
&=4x+2y+4+2\
&=4x+2y+6
end{align*}
$$

$textbf{(b)}$
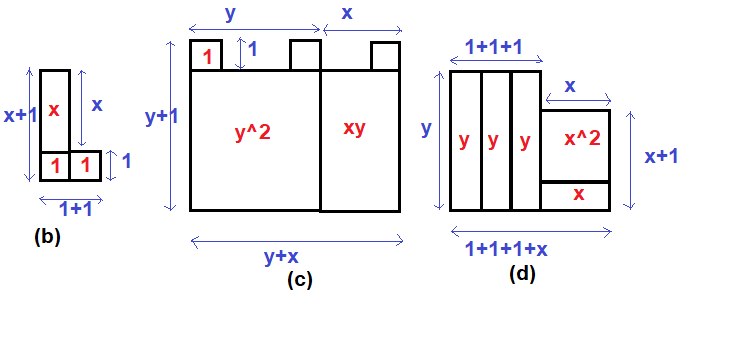
$$
begin{align*}
text{Perimeter$_b$}&= (x+1)+(1)+(x+1)+(1+1)\
&=2(x+1)+1+2\
&=2x+2+3\
&=2x+5\
end{align*}
$$

$textbf{(c)}$
$$
begin{align*}
text{Perimeter$_c$}&= (y+1)+(y+x+1+1+1+1)+(y+1)+(y+x)\
&=2(y+1)+2(y+x)+(1+1+1+1)\
&=2y+2+2y+2x+4\
&=4y+2x+6
end{align*}
$$

$textbf{(d)}$
$$
begin{align*}
text{Perimeter$_d$}&= (y)+(1+1+1+x)+(y)+(1+1+1+x)\
&=2(y)+2(1+1+1+x)\
&=2y+2x+2(3)\
&=2y+2x+6
end{align*}
$$

$textbf{(a)}$ $4x+2y+6$

$textbf{(b)}$ $2x+5$

$textbf{(c)}$ $4y+2x+6$

$textbf{(d)}$ $2y+2x+6$

The general form of any equation of line is given by $y=mx+c$, where $m$ represents the slope of the line and $c$ is the $y$-intercept of the line.

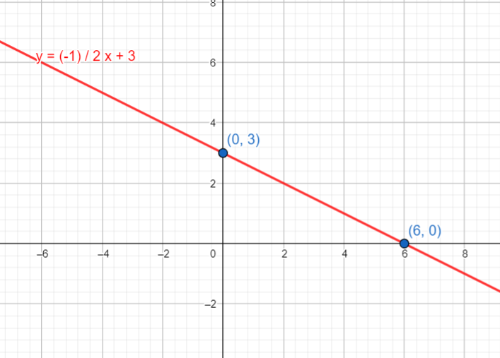
We are given the equation of line as $y=-dfrac{1}{2}x+3$

On comparing with the general form of the equation we can say the slope of the given line is $-dfrac{1}{2}$ and $y$-intercept is $3$. The graph of the given line is attached below.

Slope of the given line is $-dfrac{1}{2}$ and $y$-intercept is $3$ and the graph for the given line is attached inside.

To write the equation of line from the points given in the table we just need to choose any two set of points and we can write the equation by first finding the slope of the line from those two points and finally writing the equation of the line with this slope. The procedure is explained below.

Let the two points from the table is $(2,2)$ and $(4,3)$.

The slope of any line passing through the points $x_1,y_1$ and $(x_2,y_2)$ is given by

$$
text{Slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

Therefore, the slope of the line from the points $(2,2)$ and $(4,3)$ is given by

$$
text{Slope}=dfrac{3-2}{4-2}=dfrac{1}{2}
$$

Now, the equation of a line of given slope $m$ and which passes through a point $x_1,y_1$ is given by

$$
y-y_1=mcdot(x-x_1)
$$

Therefore, the equation of the line of slope $dfrac{1}{2}$ passing through $(2,2)$ is given by

$$
begin{align*}
y-2&=dfrac{1}{2}cdot (x-2)\
y-2&=dfrac{1}{2}cdot x + dfrac{1}{2}cdot (-2)\
y-2&=dfrac{1}{2}cdot x -1\
y&=dfrac{1}{2}cdot x -1+2\
y&=dfrac{1}{2}cdot x+1
end{align*}
$$

Therefore, the equation of line from the points given in the table is
$$
y=dfrac{1}{2}cdot x+1
$$

The equation of line from the points given in the table is $y=dfrac{1}{2}cdot x+1$

The equation in the ex 3-78 is $y=-dfrac{1}{2}+3$, and its $y$-intercept is $3$ which we can tell by comparing it with general form equation of line $y=mx+c$ where, $c$ is $y$-intercept.

Similarly, The equation in the ex 3-79 is $y=dfrac{1}{2}+1$ and it has $y$-intercept equal to $1$.
Therefore, function in ex 3-78 has the greater $y$-intercept.

Function in ex 3-78 has the greater $y$-intercept.

$textbf{(a)}$ For 90$text{textdegree}$ rotation around origin we need to interchange the coordinates of points and multiply the resultant $x$ coordinate by $-1$ for the final coordinate after rotation. For example $(x_1,y_1)$ becomes $(-y_1,x_1)$

$$
text{C}(-1,5) rightarrow text{C’}(-5,-1)
$$

The figure is attached below.

$textbf{(b)}$
$$
text{C}(-1,5) rightarrow text{C”}(3,5)
$$

$textbf{(c)}$
$$
text{C}(-1,5) rightarrow text{C”’}(11,0)
$$

The line $y=-dfrac{5}{12}+1$ is parallel to the line passing through points C and C”’.

From the figure we can see that length of the rectangle is 4 units and width is of 3 units.

The area of rectangle is given by
$$
text{Area}=text{length}times text{width}
$$

$Rightarrow$
$$
text{Area}=4times 3=12 text{ unit}^2
$$

$textbf{(a)}$ $text{C}(-1,5) rightarrow text{C’}(-5,-1)$

$textbf{(b)}$ $text{C}(-1,5) rightarrow text{C”}(3,5)$

$textbf{(c)}$ $text{C}(-1,5) rightarrow text{C”’}(11,0)$

$textbf{(d)}$ $text{Area}=4times 3=12 text{ unit}^2$

$textbf{(a)}$ Calculate the output for the input that is 4 less than $c$

$textbf{(b)}$ Calculate the output for the input that is half of $b$

$textbf{(c)}$ Calculate the output for the input $d$ and add 12 in it for the final output.

$textbf{(a)}$ Calculate the output for the input that is 4 less than $c$

$textbf{(b)}$ Calculate the output for the input that is half of $b$

$textbf{(c)}$ Calculate the output for the input $d$ and add 12 in it for the final output.

$bullet$ Perimeter of a figure is the sum of all the side lengths. So the perimeter of the given figure is

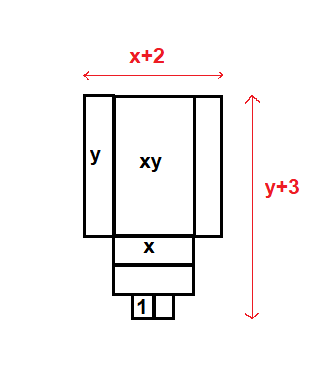
$$
begin{align*}
text{perimeter }&=1+x+1+y+1+1+1+1+1+1+1+1+1+1+1+1+y\
&=x+2y+14 text{ Unit}
end{align*}
$$

$bullet$ Area of a figure is the sum of all the individual areas in the figure

$$
begin{align*}
text{Area }&=y+xy+y+x+x+1+1\
&=xy+2y+2x+2\
&=xy+2cdot(x+y+1) text{ Unit}^2
end{align*}
$$

$text{perimeter }=x+2y+14$ Unit

$$
text{Area }=xy+2cdot(x+y+1) text{ Unit}^2
$$

$bullet$ Calculating area via sum of all its parts

$$
begin{align*}
text{Area}&=4cdot y+4cdot x+8cdot 1+xy+x^2+2cdot x\
&=4y+4x+8+xy+x^2+2x\
&=x^2+xy+6x+4y+8
end{align*}
$$

$bullet$ Calculating area via product of length and width

$$
begin{align*}
text{Area}&=(y+x+2)cdot (x+4)\
&=y(x+4)+x(x+4)+2(x+4)\
&=yx+4y+x^2+4x+2x+8\
&=x^2+xy+6x+4y+8
end{align*}
$$

We can verify that the area in both cases is the same and equal to $x^2+xy+6x+4y+8 text{ unit}^2$

$$
x^2+xy+6x+4y+8 text{ unit}^2
$$

$bullet$ Calculating area via sum of all its parts

$$
begin{align*}
text{Area}&=12cdot x+15cdot 1+8cdot x^2+10cdot x\
&=12x+15+8x^2+10x\
&=8x^2+(12+10)x+15\
&=8x^2+22x+15
end{align*}
$$

$bullet$ Calculating area via product of length and width

$$
begin{align*}
text{Area}&=(4x+5)cdot (2x+3)\
&=4x(2x+3)+5(2x+3)\
&=(8x^2+12x)+(10x+15)\
&=8x^2+12x+10x+15\
&=8x^2+22x+15
end{align*}
$$

We can verify that the area in both cases is the same and equal to $8x^2+22x+15 text{ unit}^2$

$$
8x^2+22x+15 text{ unit}^2
$$

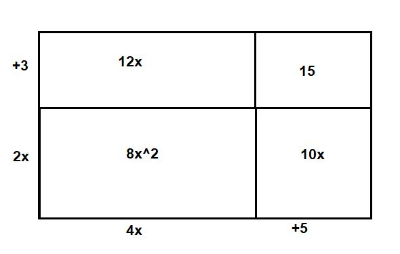
$$
textbf{(a)}
$$

$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=2x^2+3x+10x+15\
&=2x^2+13x+15
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(x+5)cdot(2x+3)
end{align*}
$$

As both represents the same area hence we can write it as shown below

$$
text{Area}=(x+5)cdot(2x+3)=2x^2+13x+15
$$

$$
textbf{(b)}
$$

$bullet$ Area as sum of its parts

$$
text{Area}=3y+15
$$

$bullet$ Area as product of the dimensions

$$
text{Area}=(3)cdot(y+5)
$$

As both represents the same area hence we can write it as shown below

$$
text{Area}=(3)cdot(y+5)=3y+15
$$

$$
textbf{(c)}
$$

$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=-42y-7x-7+24y^2+4xy+4y\
&=24y^2+4xy-38y-7x-7
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(-7+4y)cdot(6y+x+1)
end{align*}
$$

As both represents the same area hence we can write it as shown below

$$
text{Area}=(-7+4y)cdot(6y+x+1)=24y^2+4xy-38y-7x-7
$$

$$
textbf{(d)}
$$

$bullet$ Area as sum of its parts

$$
text{Area}=2x^2
$$

$bullet$ Area as product of the dimensions

$$
text{Area}=(x)cdot(2x)
$$

As both represents the same area hence we can write it as shown below

$$
text{Area}=(x)cdot(2x)=2x^2
$$

$textbf{(a)}$ $text{Area}=(x+5)cdot(2x+3)=2x^2+13x+15$

$textbf{(b)}$ $text{Area}=(3)cdot(y+5)=3y+15$

$textbf{(c)}$ $text{Area}=(-7+4y)cdot(6y+x+1)=24y^2+4xy-38y-7x-7$

$textbf{(d)}$ $text{Area}=(x)cdot(2x)=2x^2$

$textbf{(a)}$ Individual areas of each rectangle is written inside them

$textbf{(b)}$ Area of whole figure is
$$
(x+8)cdot(x+3)
$$

$textbf{(c)}$
$$
begin{align*}
text{Area}&=(x+8)cdot(x+3)\
&=x^2+3x+8x+4\
&=x^2+11x+24
end{align*}
$$

$textbf{(a)}$ See figure

$textbf{(b)}$ $(x+8)cdot(x+3)$

$textbf{(c)}$ $x^2+11x+24$

Moving expressions to the other side and solving the equation for x:

a)
$$
8x-22=-60
$$

$$
8x=-60+22
$$

$$
8x=-38
$$

$$
x=dfrac{-38}{8}
$$

$$
x=-dfrac{19}{4}
$$

Moving expressions to the other side and solving the equation for x:

b)
$$
dfrac{1}{2}x-37=-84
$$

$$
dfrac{1}{2}x=-84+37
$$

$$
dfrac{1}{2}x=-47
$$

$$
x=-47 cdot 2
$$

$$
x=-94
$$

Using $dfrac{a}{b}=dfrac{c}{d}, ; ad=bc$

c)

$$
dfrac{3x}{4}=dfrac{6}{7}
$$

$$
3x cdot 7=4 cdot 6
$$

$$
21x=24
$$

$$
x=dfrac{24}{21}
$$

$$
x=dfrac{8}{7}
$$

Moving expressions to the other side and solving the equation for x:

d)

$$
9a+15=10a-7
$$

$$
9a-10a=-7-15
$$

$$
-a=-22
$$

$$
a=22
$$

$(a) x=-dfrac{19}{4}$. See inside for the rest of the solution.

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
left(3x^2yright)left(5xright)& {=}quad : 3x^2ycdot :5xtag{Remove parentheses}\
&=15x^2xytag{Multiply the numbers} \
&=15x^{2+1}y \
&={color{#c34632}15x^3y}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad :a^bcdot :a^c=a^{b+c}
$$

$$
text{ }
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
left(x^2y^3right)left(x^{-2}y^{-2}right)& {=}quad : x^2y^3x^{-2}y^{-2}tag{Remove parentheses}\
&=x^0y^{-2}y^3\
&=x^0y\
&={color{#c34632}y}
end{align*}
$$

$$
color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad :a^bcdot :a^c=a^{b+c}
$$

$$
color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad :a^bcdot :a^c=a^{b+c}
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
frac{x^3}{x^{-2}}& {=}quad : x^{3-left(-2right)}\
&={color{#c34632}x^5}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad frac{x^a}{x^b}:=:x^{a-b}
$$

$$
text{ }
$$

$$
{color{#4257b2}text{d)}}
$$

$$
begin{align*}
left(2x^{-1}right)^3& {=}quad : left(frac{2}{x}right)^3\
&2x^{-1}=2cdot frac{1}{x}=frac{1cdot :2}{x}=frac{2}{x} tag{Simplify}\
&left(frac{2}{x}right)^3=frac{2^3}{x^3}\
&={color{#c34632}frac{8}{x^3}}
end{align*}
$$

$$
color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad :a^{-1}=frac{1}{a}
$$

$$
color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad left(frac{a}{b}right)^c=frac{a^c}{b^c}
$$

$$
color{#4257b2} text{ a) }15x^3y
$$

$$
color{#4257b2} text{ b) }y
$$

$$
color{#4257b2} text{ c) }x^5
$$

$$
color{#4257b2}text{ d) }frac{8}{x^3}
$$

Let $x$ represents the number of weeks and y represents her account’s worth, then we can represent the situation in the equation as shown below.

$$
begin{align*}
y&=1500-35x
end{align*}
$$

Now solving for the number of weeks when her account has only 915$

$$
begin{align*}
915&=1500-35x\
35x&=1500-915\
x&=dfrac{585}{35}\
x&=16.71 text{ weeks}
end{align*}
$$

We need to get the area of the triangle with a known coordinates of the vertices $color{#4257b2} A(8, -4), B(8, 1)$ and $color{#4257b2}C(2, 0)$ using the formula:

$color{#c34632} A= dfrac{1}{2} [ x_1 (y_2- y_3) + x_2 (y_3- y_1)+ x_3 (y_1- y_2)]$

Substitute with $x_1 = 8, x_2=2, x_3 =8, y_1= 1, y_2= 0$ and $y_3=-4$ in the formula of the area.

$$
A= dfrac{1}{2} [ 8(0-(-4)) +2(-4-1) + 8(1-0)] = dfrac{1}{2} [ 8(4)+2(-5)+8(1)]= dfrac{1}{2} [32-10+8] = dfrac{1}{2} (30)= boxed{ 15}
$$

b) Triangle ABC is rotated about the origin $180 text{textdegree}$ to become A’B’C’ as shown in gragh.

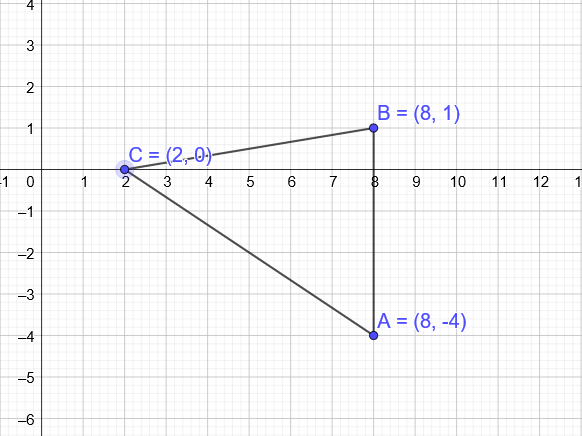
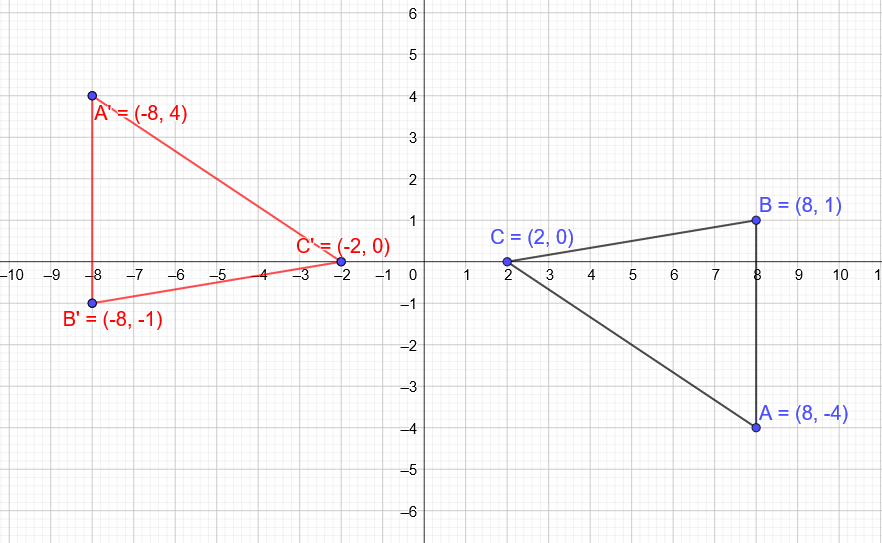
$(x, y) Rightarrow (-x, -y)$
$A(8, -4) Rightarrow A'(-8, 4)$

$B(8, 1) Rightarrow B'(-8, -1)$

$C(2, 0) Rightarrow C'(-2, 0)$

The coordinates of point B” as shown in gragh $B”(-4, -1)$

d) b) Triangle ABC is rotated about the origin $90 text{textdegree}$ clockwise to become A'”B”‘C'” as shown in gragh.

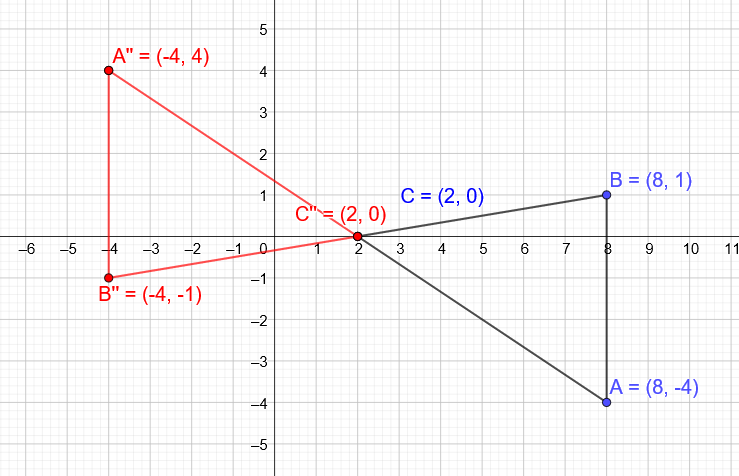
$(x, y) Rightarrow (y, -x)$
$A(8, -4) Rightarrow A”‘(-4, -8)$

a)$15$

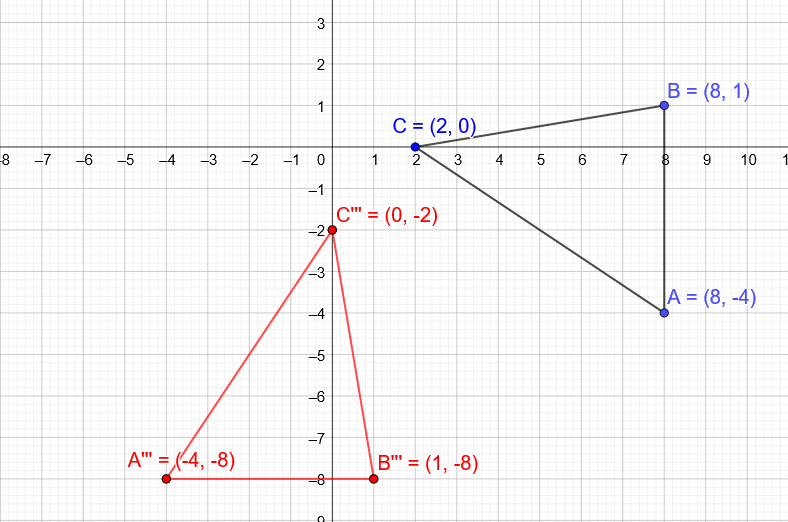
b) $A'(-8, 4), B'(-8, -1), C'(-2, 0)$

c) $B”(-4, -1)$

D) $A”'(-4, -8)$

For graphing the line, we need at least two points on the given line. We can find the points on the line by choosing any value for one variable and solve for other.
For example let $x=0$, is $x$ coordinates of point then we can solve for $y$ by putting $x=0$ in $y=dfrac{3}{4}x$ which gives $y=0$ hence one point on the line is $(0,0)$. Similarly, let $x=4$ then $y=dfrac{3}{4}cdot 4=3$, hence another point is $(4,3)$. We can mark these two points on the graph and draw a straight line passing through them, which will give our desired graph of the our line.

$textbf{(a)}$ Slope triangle is shown in the figure attached above.

$textbf{(b)}$ The slope of the resultant line will be perpendicular to the given slope hence is will be given by

$$
text{Slope}bot=dfrac{-1}{dfrac{3}{4}}=-dfrac{4}{3}
$$

$textbf{(c)}$ Line perpendicular to line $y=dfrac{4}{3}x$ will have slope $-dfrac{3}{4}$. So, It can be any line with the slope $-dfrac{3}{4}$.
The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

Lets assume the new line passes through $(4,1)$, therefore, the equation of a line of given slope $-dfrac{3}{4}$ passing through a point $1,4$ is given by

$$
begin{align*}
y-(1)&=-dfrac{3}{4}cdot (x-4)\
y-1&=-dfrac{3}{4}cdot x+-dfrac{3}{4}cdot(-4) \
y-1&=-dfrac{3}{4}cdot x +3\
y&=-dfrac{3}{4}cdot x +4\
end{align*}
$$

$textbf{(b)}$ $-dfrac{4}{3}$

$textbf{(c)}$ Any line with the slope $-dfrac{3}{4}$ will be perpendicular to the line $y=dfrac{4}{3}x$, the equation will change according to the $y$-intercepts only.See inside for an example

$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=-x^2+xy+2x+4x-4y-8\
&=-x^2+xy+6x-4y-8
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(x-4)cdot(y-x+2)\
&=x(y-x+2)+-4(y-x+2)\
&=(xy-x^2+2x) + (-4y+4x-8)\
&=-x^2+xy + (2x+4x) -4y-8\
&=-x^2+xy+6x-4y-8
end{align*}
$$

We can see that Area from both the cases are the same hence, we can write it as shown below.

$$
text{Area}=(x-4)cdot(y-x+2)=-x^2+xy+6x-4y-8
$$

$$
text{Area}=(x-4)cdot(y-x+2)=-x^2+xy+6x-4y-8
$$

$textbf{(a)}$
$$
text{Area$_a$}=(x+3)cdot (2x+1)=2x^2+6x+x+3
$$

$textbf{(b)}$
$$
text{Area$_b$}=(2x)cdot (x+5)=2x^2+10x
$$

$textbf{(c)}$
$$
text{Area$_c$}=(x)cdot (2x-y)=2x^2-xy
$$

$textbf{(d)}$
$$
text{Area$_d$}=(2x+5)cdot (x+y+2)=2x^2+5x+2xy+5y+4x+10
$$

$textbf{(e)}$
$$
text{Area$_e$}=(2x-1)cdot (2x-1)=4x^2-2x-2x+1
$$

$textbf{(f)}$
$$
text{Area$_f$}=(2x)cdot (4x)=8x^2
$$

$textbf{(g)}$
$$
text{Area$_g$}=(2)cdot (3x-5)=6x-10
$$

$textbf{(h)}$
$$
text{Area$_h$}=(y)cdot (2x+y+3)=2xy+y^2+3y
$$

$textbf{(a)}$ $text{Area$_a$}=(x+3)cdot (2x+1)=2x^2+6x+x+3$

$textbf{(b)}$ $text{Area$_b$}=(2x)cdot (x+5)=2x^2+10x$

$textbf{(c)}$ $text{Area$_c$}=(x)cdot (2x-y)=2x^2-xy$

$textbf{(d)}$ $text{Area$_d$}=(2x+5)cdot (x+y+2)=2x^2+5x+2xy+5y+4x+10$

$textbf{(e)}$ $text{Area$_e$}=(2x-1)cdot (2x-1)=4x^2-2x-2x+1$

$textbf{(f)}$ $text{Area$_f$}=(2x)cdot (4x)=8x^2$

$textbf{(g)}$ $text{Area$_g$}=(2)cdot (3x-5)=6x-10$

$textbf{(h)}$ $text{Area$_h$}=(y)cdot (2x+y+3)=2xy+y^2+3y$

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
2xleft(6x+5right)& {=}quad : 2xcdot :6x+2xcdot :5\
&={color{#c34632}12x^2+10x}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad :aleft(b+cright)=ab+ac
$$

$$
color{#c34632} text{ } a=2x,:b=6x,:c=5
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
6left(4x+1right)& {=}quad :6cdot :4x+6cdot :1\
&={color{#c34632}24x+6}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad :aleft(b+cright)=ab+ac
$$

$$
color{#c34632} text{ }a=6,:b=4x,:c=1
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
3yleft(4x+3right)& {=}quad : 3ycdot :4x+3ycdot :3\
&={color{#c34632}12yx+9y}
end{align*}
$$

$$
color{#c34632}text{ }mathrm{Distribute:parentheses:using}:quad :aleft(b+cright)=ab+ac
$$

$$
color{#c34632} text{ } a=3y,:b=4x,:c=3
$$

$$
{color{#4257b2}text{d)}}
$$

$$
begin{align*}
7yleft(10x+11yright)& {=}quad :7ycdot :10x+7ycdot :11y\
&={color{#c34632}70yx+77y^2}
end{align*}
$$

$$
color{#c34632}text{ }mathrm{Distribute:parentheses:using}:quad :aleft(b+cright)=ab+ac
$$

$$
color{#c34632} text{ }a=7y,:b=10x,:c=11y
$$

$$
color{#4257b2} text{ a) }12x^2+10x
$$

$$
color{#4257b2} text{ b) }24x+6
$$

$$
color{#4257b2}text{ c) }12yx+9y
$$

$$
color{#4257b2}text{ d) }70yx+77y^2
$$

No, order doesn’t matter when multiplying polynomials.

$textbf{(a)}$ Yes, $(x+1)(7x+1)$ and $(7x+1)(x+1)$ are the equivalent expressions which has same value of area which is equal to $7x^2+7x+x+1=7x^2+8x+1$. Area model is attached below for the better explanation.
Moreover, This can be also explained using $textbf{Commutative property}$ of the multiplication, which states that
$ab=ba$.

$textbf{(b)}$ No, $(x-1)(7x+1)$ and $(1-x)(7x+1)$ are not the equivalent expressions.
$$
(x-1)(7x+1)=7x^2+x+-7x-1=7x^2-6x-1
$$

$$
(1-x)(7x+1)=7x+1-7x^2-x=-7x^2+6x+1
$$
Therefore, algebraically we can see that those expressions are not equivalent. Area model is attached below for the better explanation.
Moreover, This cannot be explained by using $textbf{Commutative property}$ of the multiplication, as $(x-1)$ and $(1-x)$ are different multipliers.

$textbf{(c)}$

$$
textbf{(i.)}
$$

$$
begin{align*}
&(x – 5)(2x + 3)\
&=x(2x + 3)+ -5(2x + 3)\
&=(2x^2+3x) +(-10x-15)\
&=2x^2+3x-10x-15\
&=2x^2-7x-15
end{align*}
$$

$$
textbf{(ii.)}
$$

$$
begin{align*}
&(5 – x)(2x + 3)\
&=5(2x + 3)+ -x(2x + 3)\
&=(10x+15) +(-2x^2-3x)\
&=10x+15-2x^2-3x\
&=-2x^2+7x+15
end{align*}
$$

$$
textbf{(iii.)}
$$

$$
begin{align*}
&(2x – 3)(x + 5)\
&=2x(x + 5)+ -3(x + 5)\
&=(2x^2+10x) +(-3x-15)\
&=2x^2+10x-3x-15\
&=2x^2+7x-15
end{align*}
$$

$$
textbf{(iv.)}
$$

$$
begin{align*}
&(2x + 3)(x – 5)\
&=2x(x – 5)+3(x – 5)\
&=(2x^2-10x) +(3x-15)\
&=2x^2-10x+3x-15\
&=2x^2-7x-15
end{align*}
$$

$$
textbf{(v.)}
$$

$$
begin{align*}
&(-2x + 3)(x + 5)\
&=-2x(x +5)+3(x + 5)\
&=(-2x^2-10x) +(3x+15)\
&=-2x^2-10x+3x+15\
&=-2x^2-7x+15
end{align*}
$$

$$
textbf{(vi.)}
$$

$$
begin{align*}
&(-5 + x)(2x + 3)\
&=-5(2x + 3)+ x(2x + 3)\
&=(-10x-15) +(2x^2+3x)\
&=-10x-15+2x^2+3x\
&=2x^2-7x-15
end{align*}
$$

$$
textbf{(vii.)}
$$

$$
begin{align*}
&(-x+5)(2x + 3)\
&=-x(2x + 3)+ 5(2x + 3)\
&=(-2x^2-3x) +(10x+15)\
&=-2x^2-3x+10x+15\
&=-2x^2+7x+15
end{align*}
$$

$$
textbf{(viii.)}
$$

$$
begin{align*}
&(2x+3)(5-x)\
&=2x(5-x)+3(5-x)\
&=(10x-2x^2) +(15-3x)\
&=10x-2x^2+15-3x\
&=-2x^2+7x+15
end{align*}
$$

Now, comparing the final expressions of each part in the option (c), we can say that

$textbf{(i.)}$, $textbf{(iv.)}$ and $textbf{(vi.)}$ are equal with each other

$textbf{(ii.)}$, $textbf{(vii.)}$ and $textbf{(viii.)}$ are equal with each other

No, order doesn’t matter when multiplying polynomials.

$textbf{(a)}$ Yes, $(x+1)(7x+1)$ and $(7x+1)(x+1)$ are the equivalent expressions

$textbf{(b)}$ No, $(x-1)(7x+1)$ and $(1-x)(7x+1)$ are not the equivalent expressions.

$textbf{(c)}$ Expressions (i.), (iv.) and(vi.) are equal with each other

Expressions (ii.), (vii.) and (viii.) are equal with each other

Figure is attached above in which mentioned data is shown in the blue colours and the missing values are shown in the red colour. For finding the missing values, we need to analyse the given data which will some of the dimensions fixed then then we need to adjust the values of the missing dimensions or areas so that is satisfy the given data. In some cases there are more than one possible values for the missing data because of the lack of the sufficient data to make it unique figure. Such options are specified clearly while solving for the area of the whole figure.

$textbf{(a)}$ The dimensions will be unique which is $(x+3)$ and (y) for the given areas in the figure.

$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=xy+3y
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(x+3)cdot(y)\
&=x(y)+3(y)\
&=xy+3y
end{align*}
$$

$textbf{(b)}$ From the given data, the possible dimension will be unique which is $(x+5)$ and $(x+12)$, and so will be missing areas also will be unique.

$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=x^2+5x+12x+60\
&=x^2+17x+60
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(x+5)cdot(x+12)\
&=x(x+12)+5(x+12)\
&=(x^2+12x) + (5x+60)\
&=x^2+17x+60
end{align*}
$$

$textbf{(c)}$ From the given data, the possible dimension will be unique which is $(2x-3y+5)$ and $(x-2)$, and so will be missing areas also will be unique.

$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=2x^2-3xy+5x-4x+6y-10\
&=2x^2-3xy+x+6y-10
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(x-2)cdot(2x-3y+5)\
&=x(2x-3y+5)+-2(2x-3y+5)\
&=(2x^2-3xy+5x) + (-4x+6y-10)\
&=2x^2-3xy+x+6y-10
end{align*}
$$

$textbf{(d)}$ From the given data, there will be more than one possible dimensions for the missing values which can be $(x+1); (x+2); (x+3)cdots$ for horizontal length and $(x+6); (x+3); (x+2)$ for vertical length, and hence the area will also change accordingly.

In the figure, two possible values of dimensions and areas are shown in red and green colours.

$textbf{(a)}$ The dimensions will be unique which is $(x+3)$ and (y) for the given areas in the figure.

$textbf{(b)}$ From the given data, the possible dimension will be unique which is $(x+5)$ and $(x+12)$, and so will be missing areas also will be unique which is $x^2+17x+60$

$textbf{(c)}$ From the given data, the possible dimension will be unique which will be $(2x-3y+5)$ and $(x-2)$, and so will be missing areas also will be unique which will be $2x^2-3xy+x+6y-10$

$textbf{(d)}$ From the given data, there will be more than one possible dimensions for the missing values which can be $(x+1); (x+2); (x+3)cdots$ for horizontal length and $(x+6); (x+3); (x+2)$ for vertical length, and hence the area will also change accordingly.

$textbf{(a)}$
$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=12x^2+x-60x-5\
&=12x^2-59x-5
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(12x+1)cdot(x-5)\
&=12x(x-5)+1(x-5)\
&=(12x^2-60x) + (x-5)\
&=12x^2-60x+x-5\
&=12x^2-59x-5
end{align*}
$$

We can see that Area from both the cases are the same hence, we can write it as shown below.

$$
text{Area}=(12x+1)cdot(x-5)=12x^2+x-60x-5
$$

$textbf{(b)}$
$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=6m^3-12m^2-3m+10m^2-20m-5\
&=6m^3-2m^2-35m-5
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(3m+5)cdot(2m^2-4m-1)\
&=3m(2m^2-4m-1)+5(2m^2-4m-1)\
&=(6m^3-12m^2-3m) + (10m^2-20m-5)\
&=6m^3-12m^2+10m^2 -3m-20m-5\
&=6m^3-2m^2-35m-5
end{align*}
$$

We can see that Area from both the cases are the same hence, we can write it as shown below.

$$
text{Area}=(3m+5)cdot(2m^2-4m-1)=6m^3-2m^2-35m-5
$$

$textbf{(c)}$
$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=2x^2+5x+12x+30\
&=2x^2+17x+30
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(2x+5)cdot(x+6)\
&=2x(x+6)+5(x+6)\
&=(2x^2+12x) + (5x+30)\
&=2x^2+12x+5x+30\
&=2x^2+17x+30
end{align*}
$$

We can see that Area from both the cases are the same hence, we can write it as shown below.

$$
text{Area}=(2x+5)cdot(x+6)=2x^2+17x+30
$$

$textbf{(d)}$
$bullet$ Area as sum of its parts

$$
begin{align*}
text{Area}&=6-10y+3y-5y^2\
&=-5y^2-10y+3y+6\
&=-5y^2-7y+6
end{align*}
$$

$bullet$ Area as product of the dimensions

$$
begin{align*}
text{Area}&=(3-5y)cdot(2+y)\
&=3(2+y)-5y(2+y)\
&=(6+3y) + (-10y-5y^2)\
&=6+3y-10y -5y^2\
&=-5y^2-7y+6
end{align*}
$$

We can see that Area from both the cases are the same hence, we can write it as shown below.

$$
text{Area}=(3-5y)cdot(2+y)=-5y^2-7y+6
$$

$textbf{(a)}$ $text{Area}=(12x+1)cdot(x-5)=12x^2+x-60x-5$

$textbf{(b)}$ $text{Area}=(3m+5)cdot(2m^2-4m-1)=6m^3-2m^2-35m-5$

$textbf{(c)}$ $text{Area}=(2x+5)cdot(x+6)=2x^2+17x+30$

$textbf{(d)}$ $text{Area}=(3-5y)cdot(2+y)=-5y^2-7y+6$

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
-4yleft(5x+8yright)& {=}quad : -4ycdot :5x-4ycdot :8y\
&-4ycdot :5x=-20yx tag{Simplify}\
&-4ycdot :8y=-32y^2 tag{Simplify}\
&={color{#c34632}-20yx-32y^2}
end{align*}
$$

$$
color{#c34632} text{ } mathrm{Distribute:parentheses:using}:quad :aleft(b+cright)=ab+ac
$$

$$
color{#c34632}text{ }a=-4y,:b=5x,:c=8y
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
9xleft(-4+10yright)& {=}quad : 9xleft(-4right)+9xcdot :10y\
&=-9xcdot :4+9xcdot :10y\
&=-36x+9cdot :10xy tag{Simplify}\
&={color{#c34632}-36x+90xy}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad :aleft(b+cright)=ab+ac
$$

$$
color{#c34632} text{ }a=9x,:b=-4,:c=10y
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
left(x^2-2right)left(x^2+3x+5right)& {=}quad : x^2x^2+x^2cdot :3x+x^2cdot :5-2x^2-2cdot :3x-2cdot :5tag{Distribute parentheses}\
&=x^2x^2+3x^2x+3x^2-2cdot :3x-2cdot :5 \
&={color{#c34632}x^4+3x^3+3x^2-6x-10}
end{align*}
$$

$$
color{#4257b2} text{ a) }-20yx-32y^2
$$

$$
color{#4257b2} text{ b) }-36x+90xy
$$

$$
color{#4257b2} text{ c) }x^4+3x^3+3x^2-6x-10
$$

$textbf{(a)}$ 90$text{textdegree}$ clockwise rotation with respect to origin can be modeled as interchanging the $x$ and $y$ coordinates and then multiplying the $y$ coordinate by $-1$. For example $(x_1, y_1)$ becomes $(y_1, -x_1)$.

$Rightarrow$
$$
text{A} (-4,3) rightarrow text{A’} (3,4)
$$

$$
text{B} (-6,1) rightarrow text{B’} (1,6)
$$

$$
text{C} (-8,5) rightarrow text{C’} (5,8)
$$

$textbf{(b)}$ Applying the function (x, y) $rightarrow$ (x + 5, y + 1) to translate A’ B’ C’ to form A”B”C”.
We just need to put the value of the original coordinates into the function and it will give the resultant coordinates.
$Rightarrow$
$$
text{C’} (5,8) rightarrow text{C”} (5+5,8+1)=(10,9)
$$

$textbf{(a)}$ $text{A} (-4,3) rightarrow text{A’} (3,4)$

$textbf{(b)}$ $text{C’} (5,8) rightarrow text{C”}(10,9)$

$textbf{(a)}$ The area of rectangle is given by product of its adjacent side lengths.

$$
text{Area}=text{Length}timestext{width}
$$

From the graph we can see the side length is 5 units and width is 4 units.
Therefore, its area is given by

$$
text{Area}=5times 4=20 text{ Unit}^2
$$

$textbf{(b)}$ The area of rectangle is given by product of its adjacent side lengths.

$$
text{Area}=text{Length}timestext{width}
$$

Given that Shirley’s points are: $(352,150)$, $(352,175)$, $(456,150)$, and $(456,175)$
As the coordinates are big and cannot expressed on the available graph paper. So, we need to find the side lengths algebraically.

We know that the distance between to given points $x1,y_1$ and $(x_2,y_2)$ can be found out as

$$
text{Distance}=sqrt{((x_2-x_1)^2+y_2-y_1)^2}
$$

Therefore, side length for the side made by points $(352,150)$ and $(352,175)$ is

$$
text{Length}=sqrt{(352-352)^2+(175-150)^2}=sqrt{0+25^2}=25
$$

Now, Other point adjacent to $(352,150)$ is $(456,150)$. Therefore, side width for the side made by points $(352,150)$ and $(456,150)$ is

$$
text{Width}=sqrt{(456-352)^2+(150-150)^2}=sqrt{104^2+0}=104
$$

Therefore, the area of the rectangle is given by

$$
text{Area}=25times 104=2600text{ unit}^2
$$

$textbf{(a)}$ $text{Area}=5times 4=20 text{ Unit}^2$

$textbf{(b)}$ $text{Area}=25times 104=2600 text{ Unit}^2$

$$
textbf{(a)}
$$

$bullet$ Solving the equation $100x+300=500$

$$
begin{align*}
100x+300&=500 tag{Subtract 300 from each side}\
100x+300-300&=500-300\
100x&=200tag{Divide both side by 100}\
dfrac{100x}{100}&=dfrac{200}{100}\
x&=2
end{align*}
$$

$bullet$ Solving the equation $x+3=5$
$$
begin{align*}
x+3&=5 tag{Subtract 3 from each side}\
x+3-3&=5-3\
x&=2
end{align*}
$$

Both the equations have same solution. hence it is verified that we can use $x+3=5$ instead of $100x+300=500$.

$textbf{(b)}$ We can divide the both side of the equation $100x+300=500$ by 100 to get $x+3=5$. Steps are shown below

$$
begin{align*}
100x+300&=500 tag{Divide both side by 100}\
dfrac{(100x+300)}{100}&=dfrac{500}{100}\
dfrac{100x}{100}+dfrac{300}{100}&=5\
x+3&=5
end{align*}
$$

$textbf{(a)}$ Yes, both the equations have same solution. Hence it is verified that we can use $x+3=5$ instead of $100x+300=500$.

$textbf{(b)}$ We can divide the both side of the equation $100x+300=500$ by 100 to get $x+3=5$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
&text{Remove parentheses}\
&=-frac{2}{3}-frac{1}{8}\\
& =-frac{2cdot :8}{24}-frac{1cdot :3}{24} tag{Adjust fraction} \
&=frac{-2cdot :8-1cdot :3}{24}\
&=frac{-19}{24}\\
&=boxed{{color{#c34632} -frac{19}{24} } }
end{align*}
$$

$$
color{#c34632}text{}mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=frac{7}{2}-left(-frac{4}{3}right)\\
&=frac{7}{2}+frac{4}{3} \
& =frac{7cdot :3}{6}+frac{4cdot :2}{6} tag{Adjust fraction} \
&=frac{7cdot :3+4cdot :2}{6}\
&=frac{29}{6}\\
&=boxed{{color{#c34632} 4frac{5}{6}} }
end{align*}
$$

$$
color{#c34632}text{}mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} text{}mathrm{Apply:rule}:-left(-aright)=a
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=left(-frac{21}{5}right)left(-frac{1}{3}right)\\
&=frac{21}{5}cdot frac{1}{3} tag{Remove parentheses} \
& =frac{21cdot :1}{5cdot :3}tag{Multiply fractions} \
&=frac{21}{5cdot :3}\
&=frac{21}{15}tag{Multiply the numbers} \
&=frac{7}{5} tag{Cancel the common factor 3}\\
&=boxed{{color{#c34632} 1frac{2}{5} } }
end{align*}
$$

$$
color{#c34632}text{}mathrm{Remove:parentheses}:quad left(-aright)=-a
$$

$$
color{#c34632} text{}mathrm{Multiply:fractions}:quad frac{a}{b}cdot frac{c}{d}=frac{a:cdot :c}{b:cdot :d}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
&text{Divide fractions}\
&=-frac{2cdot :4}{3cdot :1}\\
& =-frac{2cdot :4}{3} tag{Refine} \\
&=boxed{{color{#c34632}-frac{8}{3}} } tag{Multiply the numbers}\
end{align*}
$$

$$
color{#c34632} text{}mathrm{Divide:fractions}:quad frac{frac{a}{b}}{frac{c}{d}}=frac{acdot :d}{bcdot :c}
$$

$$
{color{#4257b2}text{ e) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=frac{7}{4}+left(-frac{16}{3}right)\\
&=frac{7}{4}-frac{16}{3} tag{Remove parentheses} \
& =frac{7cdot :3}{12}-frac{16cdot :4}{12} tag{Adjust fraction} \
&=frac{7cdot :3-16cdot :4}{12}\
&=frac{-43}{12}\
&=-frac{43}{12}\\
&=boxed{{color{#c34632} -3frac{7}{12} } }
end{align*}
$$

$$
color{#c34632}text{}mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b}
$$

$$
{color{#4257b2}text{ f) }}
$$

$$
begin{align*}
&text{Convert mixed numbers to improper fractions}\
&=left(-frac{8}{3}right)div left(-frac{7}{6}right)\\
&=frac{8cdot :6}{3cdot :7} tag{Divide fractions} \
& =frac{8cdot :6}{21}tag{Multiply the numbers} \
&=frac{48}{21}tag{Multiply the numbers} \
&=frac{16}{7} tag{Cancel the common factor 3}\\
&=boxed{{color{#c34632} 2frac{2}{7} } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Divide:fractions}:quad frac{frac{a}{b}}{frac{c}{d}}=frac{acdot :d}{bcdot :c}
$$

$$
color{#4257b2} text{a)} -frac{19}{24}
$$

$$
color{#4257b2} text{b)} 4frac{5}{6}
$$

$$
color{#4257b2} text{c)}1frac{2}{5}
$$

$$
color{#4257b2} text{d)}-frac{8}{3}
$$

$$
color{#4257b2} text{e)} -3frac{7}{12}
$$

$$
color{#4257b2} text{f)} 2frac{2}{7}
$$

We are going to multiply each of the expressions by using Distributive property. Distributive property states that $acdot(b+c)=acdot b+acdot c$

$textbf{(a)}$
$$
begin{align*}
&(6x-11)(2x+5)\
&=6x(2x+5)-11(2x+5)\
&=(6xcdot 2x + 6xcdot 5)+(-11cdot 2x-11cdot 5)\
&=12x^2+30x-22x-55\
&=12x^2+8x-55
end{align*}
$$

$textbf{(b)}$
$$
begin{align*}
& -2x^2(15x^2-3y)\
&=-2x^2(15x^2)-2x^2(-3y) \
&=-30x^4+6x^2y tag{using $a^mcdot a^n=a^{m+n}$}
end{align*}
$$

$textbf{(a)}$ $12x^2+8x-55$

$textbf{(b)}$ $-30x^4+6x^2y$

We need to solve the equation $color{#4257b2} 4(x+3) = 20$ to get the value of $x$.

* The first method : we divide the right hand side and the left hand side by $4$ to simplify the equation.

$Rightarrow x+3 = dfrac{20}{4} Rightarrow x+3 = 5$

subtract $(3)$ from both sides to get the value of $x$ $Rightarrow x= 5-3 Rightarrow color{#c34632} boxed{ x=2}$

* The second method : we multiply $(4)$ times each term of the bracket to simplify the equation.

$Rightarrow 4x+12 = 20$

Subtract $(12)$ from both sides $Rightarrow 4x= 20-12 Rightarrow 4x= 8$

Divide both sides by $(4)$ $Rightarrow x= dfrac{8}{4} Rightarrow color{#c34632} boxed{ x=2}$

$$
x=2
$$

Solution using David’s method is shown below.

$$
begin{align*}
4(x+3)&=20 tag{ multiply using distributive property}\
4x+12&=20 tag{Subtract 12 from each side}\
4x+12-12&=20-12\
4x&=8tag{divide each side by 4}\
dfrac{4x}{4}&=dfrac{8}{4}\
x&=2
end{align*}
$$

Therefore, new equation will be $4x+12=20$ and solution of it will be $x=2$

The new equation will be $4x+12=20$ and solution of it will be $x=2$

$textbf{(a)}$ Juan is thinking of dividing the both sides of the equation with 4. This will eliminate the factor of 4 from each side. This works as dividing each side by any number which is not zero will not change the solution of the equation.

$textbf{(b)}$
$$
begin{align*}
4(x+3)&=20 tag{Divide each side by 4}\
dfrac{4(x+3)}{4}&=dfrac{20}{4}\
x+3&=5tag{subtract 3 from each side}\
x+3-3&=5-3\
x&=2
end{align*}
$$

Yes, his solution matches with the David’s solution.

$textbf{(c)}$ It is appropriate to call it undoing as the factor of 4 is getting removed from each side which makes equation simple and in its basic form which is free from any unnecessary factors.

$textbf{(a)}$ Juan is thinking of dividing the both sides of the equation with 4.

$textbf{(b)}$ Yes, his solution matches with the David’s solution.

$textbf{(c)}$ It is appropriate to call it undoing as the factor of 4 is getting removed from each side which makes equation simple and in its basic form which is free from any unnecessary factors.

$textbf{(a)}$ We can write 20 as $4cdot 5=4(5)$. Using this we can rewrite the equation as

$$
4(x+5)=4(5)
$$

On comparing the both side, one can easily see that the factor $(x+5)$ should be equal to the factor $(5)$.

$textbf{(b)}$
$$
begin{align*}
4(x+3)&=20\
4(x+3)&=4(5)\
Rightarrow\
x+3&=5 tag{subtract 3 from each side}\
x+3-3&=5-3\
x&=2
end{align*}
$$

Yes, we got the same result as with David’s method.

$textbf{(a)}$ We can write 20 as $4cdot 5=4(5)$. Using this we can rewrite the equation as
$4(x+5)=4(5)$ On comparing the both side, one can easily see that the factor $(x+5)$ should be equal to the factor $(5)$

$textbf{(b)}$ Yes, we got the same result as with David’s method.

* This problem might be easier if I turned $4(2x-3)=31$ into $8x-12=31$ that means we rewrite the equation without changing of any sides and that matches the choose $1$ from the left column.

$1) c$

* If $5^{8x} = 5^{24}$ , then $8x$ must equal $24$ and that means we use power equality theory which required to looking inside the equation to apply it and that matches the choose $2$ from the left column.

$2) a$

* Subtracting is the opposite of adding, so
for the equation $3(x – 7) + 4 = 23$, I can start by subtracting $4$ from both sides, doing the inverse process means undoing and that matches the choose $3$ from the left column.

$3) b$

$1) c$

$2) a$

$3) b$

$textbf{(a)}$
$$
begin{align*}
5x^2 +43&=(x-1)(5x+6)\
5x^2 +43&=xcdot (5x+6) -1cdot (5x+6) tag{Using distributive property}\
5x^2 +43&=(5x^2+6x)+ (-5x-6) tag{Solving brackets}\
5x^2 +43&=5x^2+6x -5x-6\
5x^2 +43&=5x^2+x-6 tag{Subtract $5x^2$ from each side}\
5x^2-5x^2 +43&=5x^2-5x^2+x-6\
43&=x-6 tag{add 6 to each side}\
43+6&=x-6+6\
49&=x tag{interchange sides}\
x&=49
end{align*}
$$

Now, checking the solution into the original equation.

$$
begin{align*}
5x^2 +43&=(x-1)(5x+6)\
5(49)^2 +43&=((49)-1)(5cdot(49)+6)\
5(2401)+43&=48(245+6)\
12005+43&=48(251)\
12048&=12048
end{align*}
$$

We can see that the solution $x=49$ satisfies the original equation.

$textbf{(b)}$
$$
begin{align*}
(x+3)^2 &=x^2 -3(1-x) tag{Use $(a+b)^2=a^2+2ab +b^2$}\
x^2+6x+9&=x^2 -3(1-x) tag{Solve brackets on RHS}\
x^2+6x+9&=x^2 -3+3x tag{Subtract $x^2$ from each side}\
x^2-x^2+6x+9&=x^2-x^2 -3+3x \
6x+9&=x-3tag{Subtract $3x$ from each side}\
6x-3x+9&=3x-3x-3\
3x+9&=-3tag{add -9 to each side}\
3x+9-9&=-3 -9
3x&=12tag{divide each side by 3}\
dfrac{3}{3}x&=dfrac{-12}{3}\
x&=-4
end{align*}
$$

Now, checking the solution into the original equation.

$$
begin{align*}
(x+3)^2& =x^2 -3(1-x)\
((-4)+3)^2 &=(-4)^2 -3(1-(-4))\
{-1}^2&=(-4)^2 -3(5)\
1&=16-15\
1&=1
end{align*}
$$

We can see that the solution $x=-4$ satisfies the original equation.

$textbf{(c)}$
$$
begin{align*}
-2(-2x^2+x-5)&=(dfrac{8x}{4y})^2cdot dfrac{1}{y^{-2}}\
4x^2-2x+10&=dfrac{64x^2}{16y^2}cdot dfrac{1}{y^{-2}} tag{Solving brackets on both sides}\
4x^2-2x+10&=dfrac{64x^2}{16y^2}cdot y^2 tag{using $a^{-m}=dfrac{1}{a^m}$}\
4x^2-2x+10&=dfrac{64}{16}cdot dfrac{y^2}{y^2}cdot x^2 \
4x^2-2x+10&=4x^2 tag{subtract $4x^2$ from each side}\
4x^2-4x^2 -2x+10&=4x^2-4x^2\
-2x+10&=0 tag{add $2x$ to each side}\
-2x+2x +10&=0+2x\
10&=2x tag{interchange sides and divide by 2 }\
dfrac{2x}{2}&=dfrac{10}{2}\
x&=5
end{align*}
$$

Now, checking the solution into the original equation.

$$
begin{align*}
-2(-2x^2+x-5)&=(dfrac{8x}{4y})^2cdot dfrac{1}{y^{-2}}\
-2(-2(5)^2+(5)-5)&=(dfrac{8(5)}{4y})^2cdot dfrac{1}{y^{-2}}\
-2(-2(5)^2+(5)-5)&=dfrac{64}{16}cdot dfrac{y^2}{y^2}cdot (5)^2 \
-2(-50+5-5)&=4cdot 25\
-2(-50)&=100\
100&=100
end{align*}
$$

We can see that the solution $x=-4$ satisfies the original equation.

$textbf{(a)}$ $x=49$

$textbf{(b)}$ $x=-4$

$textbf{(c)}$ $x=5$

$textbf{a.}$

The GCF of the terms in the equation is 4000 so we can divide both sides by 4000 to obtain an equivalent equation:

$$
dfrac{4000x-8000}{4000}=dfrac{16000}{4000}
$$

which simplifies to:

$$
color{#c34632}x-2=4
$$

$textbf{b.}$

Using the original equation, add 8000 to both sides:

$$
4000x=24000
$$

Divide both sides by 4000:

$$
x=6
$$

Using the equivalent equation, add 2 to both sides:

$$
x=6
$$

As shown, both equations gave a solution of $x=6$ so they are equivalent.

$textbf{c.}$

The GCF of the terms in the equation is 100 so we can multiply both sides by 100 to obtain an equivalent equation:

$$
left(dfrac{x}{100}+dfrac{3}{100}right)(100)= dfrac{8}{100}(100)
$$

which simplifies to:

$$
color{#c34632}x+3=8
$$

Solve the equation. Subtract 3 from both sides:

$$
color{#c34632}x=5
$$

a. $x-2=4$

b. Both equations give a solution of $x=6$.

c. $x+3=8$ ; $x=5$

The perimeter of a rectangle is equal to 2 times the sum of its any two adjacent sides.
Equation $textbf{(c)}$ represents this fact.

$bullet$ Solving for $x$

$$
begin{align*}
120&=2(6x-1)+2(2x+5)\
120&=12x-2 +4x+10\
120&=16x+8 tag{text{subtracting 8 from both side and rearraging}}\
x&=dfrac{112}{16}\
x&=7
end{align*}
$$

$$
x=7
$$

Using
$(a^n)^m=a^{mn}$ and $dfrac{a^m}{a^n}=a^{m-n}$

a)
$$
3(2x^3)^2=3(2^2x^{3 cdot 2})=3(4x^6)=12x^6
$$

Yes, this is equivalent.

b)
$$
(6x^8)(2x^{-2})=6 cdot 2 cdot x^{8+(-2)}=12x^6
$$
Yes, this is equivalent.

c)
$$
(144x^{12})^{1/2}=144^{1/2} cdot x^{12 cdot 1/2}=sqrt{144} cdot x^6=12x^6
$$
Yes, this is equivalent.

d)
$$
dfrac{60x^{10}y}{5x^4y}=dfrac{60}{5} x^{10-4}y^{1-1}=12x^6
$$
Yes, this equivalent.

a)
$$
3(2x^3)^2=3(2^2x^{3 cdot 2})=3(4x^6)=12x^6
$$

Yes, this is equivalent. See inside for the rest of the solution.

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
left(x+3right)left(4x+5right)& {=}quad : xcdot :4x+xcdot :5+3cdot :4x+3cdot :5\
&=4x^2+5x+3cdot :4x+3cdot :5 \
&=4x^2+5x+12x+15 \
&={color{#c34632}4x^2+17x+15}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad left(a+bright)left(c+dright)=ac+ad+bc+bd
$$

$$
color{#c34632} text{ } a=x,:b=3,:c=4x,:d=5
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
left(-2x^2-4xright)left(3x+4right)& {=}quad : -2x^2cdot :3x-2x^2cdot :4-4xcdot :3x-4xcdot :4\
&=-6x^3-8x^2-12x^2-16x \
&={color{#c34632}-6x^3-20x^2-16x}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad left(a+bright)left(c+dright)=ac+ad+bc+bd
$$

$$
color{#c34632} text{ } a=-2x^2,:b=-4x,:c=3x,:d=4
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
left(3y-8right)left(-x+yright)& {=}quad : 3yleft(-xright)+3ycdot :y-8left(-xright)-8cdot :y\
&=-3yx+3yy+8x-8y \
&={color{#c34632}-3yx+3y^2+8x-8y}
end{align*}
$$

$$
color{#c34632} text{ }mathrm{Distribute:parentheses:using}:quad left(a+bright)left(c+dright)=ac+ad+bc+bd
$$

$$
color{#c34632}text{ }a=3y,:b=-8,:c=-x,:d=y
$$

$$
{color{#4257b2}text{d)}}
$$

$$
begin{align*}
left(y-4right)left(3x+5y-2right)& {=}quad : ycdot :3x+ycdot :5y+yleft(-2right)-4cdot :3x-4cdot :5y-4left(-2right)tag{Distribute parentheses}\
&=ycdot :3x+ycdot :5y-ycdot :2-4cdot :3x-4cdot :5y+4cdot :2 \
&=3yx+5y^2-2y-12x-20y+8 \
&=5y^2+3yx-2y-20y-12x+8 tag{Group like terms} \
&={color{#c34632}5y^2+3yx-22y-12x+8}
end{align*}
$$

$$
color{#4257b2} text{ a) }4x^2+17x+15
$$

$$
color{#4257b2} text{ b) }-6x^3-20x^2-16x
$$

$$
color{#4257b2} text{ c) }-3yx+3y^2+8x-8y
$$

$$
color{#4257b2} text{ d) } 5y^2+3yx-22y-12x+8
$$

$a.$

The line’s slope equals the difference between point’s y-coordinates divided by the difference between their x-coordinates.

Assume slope between the $2$ points is given by $m$, then

$$
m=dfrac{mathrm{ difference> between >y >coordinates}}{mathrm{difference >between >x> coordinates}}
$$

Choose the first set of points on the given graph $(mathrm{y}_1,mathrm{x}_1) = (0,10)$ and $(mathrm{y}_2,mathrm{x}_2)=(4,0)$.
The slope of line passing through those points is given by
$$
begin{align*} m &=dfrac{mathrm{y_2-y_1}}{mathrm{x_2-x_1}}\
m &= dfrac{0-10}{4-0}\
&= -2.5
end{align*}
$$

Let’s choose another set of points on the same graph. Select any two points on the line of best fit. These points may or may not be actual scatter points on the graph but as long as the line seems to pass through a lot of given scattered points, that is the best-fit slope

$(mathrm{y}_3,mathrm{x}_3)=(1,8)$ and $(mathrm{y}_4,mathrm{x}_4)=(2,5.5)$

$$
begin{align*}m&= (5.5-8)/(2-1) \
&=-2.5 end{align*}
$$

For both sets of points we have very close or same value of the slope, hence the best-fit slope of the line is -2.5

Now, the equation of line with slope $-2.5$ and passing through $(0,10)$ is given by
$$
begin{align*} (mathrm{y} – 10)=-2.5(mathrm{x}-0)\
mathrm{ y}= -2.5mathrm{x}+10
end{align*}
$$

$b.$

As x stands for time on the graph and y represents the height of the sculpture with respect to time. So, to find the height 1 hour before Nicholas started measuring means putting x=-1 in the equation of line obtained above.

We have line as $mathrm{y}=-2.5mathrm{x}+10$

Now putting x=-1 in the line it gives

$$
begin{align*}
y&=-2.5(-1) +10\
&=12.5
end{align*}
$$

Because y is the height of sculpture hence its unit is in Inches.

Therefore, height=12.5 Inches

$a.$ Equation of line $mathrm{y}=-2.5mathrm{x}+10$
Slope of a line is an unitless quantity. The unit of y-intercept is Inches

$b.$ 12.5 Inches

$a.$

When April said that there is a way to eliminate the decimals from the given equation, she meant to multiply both sides of the equation by 10 so that the decimals at each side is eliminated and we have a easy equation.

Given equation is,
$$
begin{align*} 0.4(x-2)&=3.4-0.2x \\
dfrac{4(x-2)}{10}&=dfrac{34}{10}-dfrac{2x}{10}\\
4(x-2)&=34-2x &&text{(Multiplying each side by 10)}
end{align*}
$$

$b.$

$$
begin{align*}
4(x-2)&=34-2x\
4x-8&=34-2x &&text{(Distributive property)}\
4x-8 +2x&=34-2x+2x &&text{(add 2x to the each side)}\
6x-8+8&=34+8 &&text{(add 8 to the both side)}\
6x&=42\
x&=dfrac{42}{6}&&text{(divide each side by 6)}\
x&=7
end{align*}
$$

$a.$ $4(x-2)=34-2x$
$b.$ $x=7$

$textbf{(a)}$ Given equation is $-7.5x^2 +4.8x-0.3=2.5x^2 +10.02-10x^2$ we can obtain its simple and equivalent equation by removing the decimals from each side of the equation which is shown below.

$$
begin{align*}
-7.5x^2 +4.8x-0.3&=2.5x^2 +10.02-10x^2\\
-dfrac{75}{10}x^2 +dfrac{48}{10}x-dfrac{3}{10}&=dfrac{25}{10}x^2 +dfrac{1002}{100}-10x^2tag{multiply each side by 100}\\
-750x^2 +480x-30&=250x^2 +1002-1000x^2
end{align*}
$$

Hence, $-750x^2 +480x-30=250x^2 +1002-1000x^2$ is an equivalent form of the given equation which is free from fraction and decimals.
Now, solving this equation

$$
begin{align*}
-750x^2 +480x-30&=250x^2 +1002-1000x^2\
-750x^2 +480x-30&=(250x^2-1000x^2) +1002-1000x^2\
-750x^2 +480x-30&=-750x^2 +1002 tag{add $750x^2$ to the each side}\
-750x^2+750x^2 +480x-30&=-750x^2+750x^2 +1002\
480x-30&=1002tag{add 30 to each side}\
480x-30+30&=1002+30\
480x&=1032tag{divide each side by 480}\
dfrac{480}{480}x&=dfrac{1032}{480}\
x&=dfrac{1032}{480}\
x&=2.15
end{align*}
$$

$textbf{(b)}$ Given equation is $2000(x -24 )+ 5000 =18,000$ we can obtain its simple and equivalent equation by dividing each side of the equation by 1000.

$$
begin{align*}
2000(x -24 )+ 5000 &=18,000tag{divide each side by 1000}\
dfrac{2000(x -24 )+ 5000}{1000} &=dfrac{18,000}{1000}\
2(x -24 )+ 5 &=18
end{align*}
$$

Hence, $2(x -24 )+ 5 =18$ is an equivalent form of the given equation which is free from fraction and decimals.
Now, solving this equation

$$
begin{align*}
2(x -24 )+ 5 &=18 tag{solve bracket on LHS}\
2x-48+5&=18\
2x-43&=18tag{add 43 to each side}\
2x-43+43&=18+43\
2x&=61tag{divide each side by 2}\
dfrac{2}{2}x&=dfrac{61}{2}\
x&=30.5
end{align*}
$$

$textbf{(a)}$ $x=2.15$

$textbf{(b)}$ $x=30.5$

Given equation is $2000(x -24 )+ 5000 =18,000$. We can see that the each term in this equation has 1000 as a factor. We can remove this factor by dividing the whole equation by 1000 which can be termed as undoing.

$$
begin{align*}
2000(x -24 )+ 5000 &=18,000tag{divide each side by 1000}\
dfrac{2000(x -24 )+ 5000}{1000} &=dfrac{18,000}{1000}\
2(x -24 )+ 5 &=18
end{align*}
$$

$textbf{(a)}$
$$
begin{align*}
dfrac{x}{6}-dfrac{5}{8}&=4\
dfrac{x}{6}cdot 6-dfrac{5}{8}cdot 6&=4cdot 6\
x-5cdot dfrac{6}{8}&=24\
x-5cdot dfrac{3}{4}&=24\
x-dfrac{15}{4}&=24
end{align*}
$$

Yes, fractional term remains in the final equation.

$textbf{(b)}$ Equation in part (a) is $x-dfrac{15}{4}=24$ and for eliminating the fractional term from this equation we need to multiply each term by 4.

$$
begin{align*}
x-dfrac{15}{4}&=24\
xcdot 4 -dfrac{15}{4}cdot 4&=24cdot 4\
4x-15&=96tag{add 15 to each side}\
4x-15+15&=96+15\
4x&=111tag{divide each side by 4}\
dfrac{4x}{4}&=dfrac{111}{4}\
x&=27.75
end{align*}
$$

$textbf{(c)}$

$textbf{(i)}$
$$
begin{align*}
dfrac{5x}{3}+dfrac{15}{2}&=dfrac{5}{2}tag{multiply each term by 6}\
dfrac{5x}{3}cdot 6+dfrac{15}{2}cdot 6&=dfrac{5}{2}cdot 6\
5x cdot dfrac{6}{3} +15 cdot dfrac{6}{2}&=5 cdot dfrac{6}{2}\
5x cdot 2 +15 cdot 3 &=5 cdot 3\
10x+45&=15tag{subtract 45 from each side}\
10x+45-45&=15-45\
10x&=-30tag{divide each side by 10}\
dfrac{10x}{10}&=dfrac{-30}{10}\
x&=-3
end{align*}
$$

$textbf{(ii)}$
$$
begin{align*}
dfrac{5}{x}-2&=-dfrac{11}{8}tag{multiply each term by 8x}\
dfrac{5}{x}cdot 8x-2cdot 8x&=-dfrac{11}{8}cdot 8x\
5 cdot dfrac{8x}{x} -16x&=-11 cdot dfrac{8x}{8}\
5 cdot 8 -16x &=-11 cdot x\
40 -16x &=-11x tag{add 16x to each side}\
40 -16x+16x &=-11x+16x\
40&=5xtag{interchange sides}\
5x&=40 tag{divide each side by 5}\
dfrac{5x}{5}&=dfrac{40}{5}\
x&=8
end{align*}
$$

$textbf{(iii)}$
$$
begin{align*}
dfrac{7}{2x}+dfrac{3}{2}&=3.25tag{multiply each term by 2x}\
dfrac{7}{2x}cdot 2x+dfrac{3}{2} cdot 2x&=3.25cdot 2x\
7 cdot dfrac{2x}{2x} +3 cdot dfrac{2x}{2} &=6.5x\
7+3x&=6.5xtag{subtract 3x from each side}\
7+3x-3x&=6.5x-3x\
7&=3.5x tag{interchange sides}\
3.5x&=7tag{divide each side by 3.5}\
dfrac{3.5x}{3.5}&=dfrac{7}{3.5}\
x&=2
end{align*}
$$

$textbf{(a)}$ Yes, fractional term remains in the final equation.

$textbf{(b)}$ $x=27.75$

$textbf{(c)}$

$textbf{(i)}$ $x=-3$

$textbf{(ii)}$ $x=8$

$textbf{(iii)}$ $x=2$

$textbf{(a)}$

The part $textbf{(ii)}$ and $textbf{(iii)}$ of the option $textbf{(c)}$ have $x$ in the denominator, hence they cannot have $x=0$ as input value which will make one of its term as $dfrac{a}{0}$ which makes the equation not defined.

$textbf{(b)}$ when a value of $x$ is not allowed as an input then solution corresponding to this value will be not defined as we cannot have the function defined for this value. This can be explained as if there is no input then there should not be any output.

textbf{Equivalent Equations:}\

begin{center} Two equations are equivalent if all of their solutions are the same. There are several ways to change one
equation into a different, equivalent equation. Common ways include: adding the same number to both sides,
subtracting the same number from both sides, multiplying both sides by the same number, dividing both sides
by the same (non-zero) number, and rewriting one or both sides of the equation.end{center}

EXAMPLE: we need to find equivalent equation to the equation $color{blue}2x+ 1 = 3$\

By dividing each term of the equation by $3$ $Rightarrow color{red} dfrac{2x}{3} +dfrac{1}{3} =1$\

Check if the equation $dfrac{2x}{3} +dfrac{1}{3} =1$ is equivalent to $2𝑥 + 1 = 3$\

Multiply each term times $(3)$ $Rightarrow dfrac{2x}{3} {color{red} times 3} +dfrac{1}{3} {color{red} times 3} =1 {color{red} times 3}$\

$Rightarrow 2x+1 = 3$ ;;;; checked

The equivalent equation of $(2x+1=3)$ is $(dfrac{2x}{3} +dfrac{1}{3} =1)$

Solve the original equation $color{#4257b2} 2x+1 =3$ to find the value of $x$.

Subtract $1$ from both sides $Rightarrow 2x=2$

Divide both sides by $2$ $Rightarrow x= dfrac{2x}{2} Rightarrow color{#c34632} boxed{ x=1}$

We check by solving the equivalent equation $color{#4257b2} dfrac{2x}{3} +dfrac{1}{3}=1$ to find the value of $x$.

Subtract $dfrac{1}{3}$ from both sides $Rightarrow dfrac{2x}{3} = dfrac{2}{3}$

Multiply both sides by $dfrac{3}{2}$ $Rightarrow x= dfrac{2}{3} times dfrac{2x}{3} Rightarrow color{#c34632} boxed{ x=1}$

The value of $x$ of the original equation is the same value of $x$ of the equivalent equation.

$$
x=1
$$

$textbf{(a)}$
$$
begin{align*}
3000x-2000&=10000tag{divide each term by 1000}\
dfrac{3000x}{1000} dfrac{-2000}{1000}&=dfrac{10000}{1000}\
3x+-2&=10
end{align*}
$$

The equivalent simpler equation is $3x+-2=10$ . We can solve it as shown below

$$
begin{align*}
3x+-2&=10tag{add 2 to each side}\
3x+-2+2&=10+2\
3x&=12tag{divide each side by 3}\
dfrac{3x}{3}&=dfrac{12}{3}\
x&=4
end{align*}
$$

Now, checking the solution by putting $x=4$ into the original equation $3000x-2000=10000$

$$
begin{align*}
3000x-2000&=10000\
3000(4)-2000&=10000\
12000-2000&=10000\
10000&=10000
end{align*}
$$

We can see that solution $x=4$ satisfy the original equation. Hence verified.

$textbf{(b)}$
$$
begin{align*}
dfrac{-2x}{3} -dfrac{x}{7}&=17tag{multiply each term by 21}\
-2xcdot dfrac{21}{3} -xcdot dfrac{21}{7}&=17cdot 21\
-2xcdot 7 -xcdot 3 &=17cdot 21
end{align*}
$$

The equivalent simpler equation is $-2xcdot 7 -xcdot 3 =17cdot 21$ We can solve it as shown below

$$
begin{align*}
-2xcdot 7 -xcdot 3 &=17cdot 21\
-14x-3x&=17cdot 21\
-17x&=17cdot 21tag{divide each side by -17}\
dfrac{-17x}{-17}&=21 cdot dfrac{17}{-17}\
x&=-21
end{align*}
$$

Now, checking the solution by putting $x=-21$ into the original equation $dfrac{-2x}{3} -dfrac{x}{7}=17$

$$
begin{align*}
dfrac{-2x}{3} -dfrac{x}{7}&=17
dfrac{-2(-21)}{3} -dfrac{(-21)}{7}&=17\
dfrac{42}{3} -(-3)&=17\
14+3&=17\
17&=17
end{align*}
$$

We can see that solution $x=-21$ satisfy the original equation. Hence verified.

$textbf{(c)}$
$$
begin{align*}
dfrac{5}{2}x -dfrac{1}{3}&=13tag{multiply each term by 6}\
dfrac{5}{2}xcdot 6 -dfrac{1}{3}cdot 6&=13cdot 6\
dfrac{6}{2}5x -dfrac{6}{3}&=78\
15x-2&=78
end{align*}
$$

The equivalent simpler equation is $15x-2=78$ . We can solve it as shown below

$$
begin{align*}
15x-18 &=78tag{add 2 to each side}\
15x-2+2 &=78+2\
15x &=80tag{divide each side by 15}\
dfrac{15x}{15}&=dfrac{80}{15}\
x&=dfrac{16}{3}\
x&=5.334
end{align*}
$$

Now, checking the solution by putting $x=dfrac{16}{3}$ into the original equation $dfrac{5}{2}x -dfrac{1}{3}=13$

$$
begin{align*}
dfrac{5}{2}x -dfrac{1}{3}&=13\
dfrac{5}{2}(dfrac{16}{3}) -dfrac{1}{3}&=13\
dfrac{40}{3}-dfrac{1}{3}&=13\
dfrac{40-1}{3}&=13\
dfrac{39}{3}&=13\
13&=13
end{align*}
$$

We can see that solution $x=dfrac{16}{3}$ satisfy the original equation. Hence verified.

$$
textbf{(d)}
$$

$$
begin{align*}
dfrac{3}{10} +dfrac{2x}{5}&=dfrac{1}{2} tag{multiply each term by 10}\
dfrac{3}{10}cdot 10 +dfrac{2x}{5}cdot 10&=dfrac{1}{2}cdot 10\
dfrac{10}{10}cdot 3 +dfrac{10}{5}cdot 2x&=dfrac{10}{2}cdot 1\
3+2cdot 2x&=5\
3+4x&=5
end{align*}
$$

The equivalent simpler equation is $3+4x=5$ . We can solve it as shown below

$$
begin{align*}
3+4x&=5 tag{subtract 3 from each side}\
3-3+4x&=5-3\
4x&=2tag{divide each side by 4}\
dfrac{4x}{4}&=dfrac{2}{4}\
x&=dfrac{1}{2}
end{align*}
$$

Now, checking the solution by putting $x=dfrac{1}{2}$ into the original equation $dfrac{3}{10} +dfrac{2x}{5}=dfrac{1}{2}$

$$
begin{align*}
dfrac{3}{10} +dfrac{2x}{5}&=dfrac{1}{2}\
dfrac{3}{10} +dfrac{2(dfrac{1}{2})}{5}&=dfrac{1}{2}\
dfrac{3}{10} +dfrac{1}{5}&=dfrac{1}{2}\
dfrac{3cdot 1+1cdot 2}{10}&=dfrac{1}{2}\
dfrac{5}{10}&=dfrac{1}{2}\
dfrac{1}{2}=dfrac{1}{2}
end{align*}
$$

We can see that solution $x=dfrac{1}{2}$ satisfy the original equation. Hence verified.

$textbf{(a)}$ $x=4$

$textbf{(b)}$ $x=-21$

$textbf{(c)}$ $x=dfrac{16}{3}$

$textbf{(d)}$ $x=dfrac{1}{2}$

For the equation for the line of best fit we need to find the appropriate points on the graph that can represent the given data points on the graph with the equal number of data points above and below the line of best fit so that residuals are small and approximately equal for points above and below the line as we move on the axis.

Keeping in mind the above conditions the points $(10,14)$ and $(20,22)$ seems desirable.

$textbf{(a)}$

Slope of a line which passes through a pair or points $(x_1,y_1)$ and $(x_2,y_2)$ is given by

$$
text{slope}=dfrac{y_2-y_1}{x_2-x_1}
$$

The equation of a line of given slope $m$ passing through a point $(x_1,y_1)$ is given by

$$
y-y_1=mcdot (x-x_1)
$$

where, $y$ represents the mass of chain in grams and $x$ is the length of chain in inches.
Now, we have given points as $(10,14)$ and $(20,22)$. Let $(x_1,y_1)=(10,14)$ and $(x_2,y_2)=(20,22)$, therefore slope of line passing through these point is
$$
begin{align*}
text{slope}&= dfrac{22-14}{20-10}\
&=dfrac{8}{10}\
&=dfrac{4}{5}
end{align*}
$$

Now, the equation of a line of slope $dfrac{4}{5}$ passing through a point $(10,14)$ is given by

$$
begin{align*}
y-(14)&=dfrac{4}{5}cdot (x-10)\
y-14&=dfrac{4}{5}cdot x + dfrac{4}{5}cdot (-10)\
y-14&=dfrac{4}{5}cdot x -8 tag{add 14 to each side}\
y-14+14&=dfrac{4}{5}cdot x -8 +14\
y&=dfrac{4}{5}cdot x+ 6\
end{align*}
$$

$textbf{(b)}$ For mass of 26-inch chain we need to put the value of variable $x$ equal to 26 in the equation of line of best fit.

$$
begin{align*}
y&=dfrac{4}{5}cdot x+ 6\
y&=dfrac{4}{5}cdot(26)+ 6\
y&=dfrac{4cdot 26}{5}+6\
y&=20.8+6\
y&=26.8
end{align*}
$$

Therefore, the mass of the chain of length 26 inches is approximately equal to 26.8 inches.

$textbf{(a)}$ $y=dfrac{4}{5}+6$

$textbf{(b)}$ The mass of the chain of length 26 inches is approximately equal to 26.8 grams.

$textbf{(a)}$For 180$text{textdegree}$ rotation about origin we need to just multiply the each of $x$ and $y$ coordinates of the given $Delta$ABC with $-1$

$Rightarrow$
$text{A}(6,3) rightarrow text{A’} (-6,-3)$

$text{B}(2,1) rightarrow text{B’} (-2,-1)$

$$
text{C}(5,7) rightarrow text{C’} (-5,-7)
$$

The graph of $Delta$ABC and $Delta$A’B’C’ is shown below.

$textbf{(b)}$ For this particular rotation we don’t have some predefined algebraic transition. we need to draw the points on the graph and then guess the points according to distance from the point C and rotation of 180$text{textdegree}$.
The graph of the rotation is attached below.

$text{B}(2,1) rightarrow text{B’} (8,13)$

$textbf{(c)}$For the clockwise rotation of any coordinate point around origin, we need to interchange the coordinates then multiply the resultant $y$ coordinate with $-1$ for the final resultant. For example $(x_1,y_1)$ will become $(y_1,-x_1)$

$Rightarrow$
$text{A}(6,3) rightarrow text{A”’} (3,-6)$

$text{B}(2,1) rightarrow text{B”’} (1,-2)$

$$
text{C}(5,7) rightarrow text{C”’} (7,-5)
$$

The graph of $Delta$ABC and $Delta$A”’B”’C”’ is shown below.

$textbf{(a)}$
$text{A}(6,3) rightarrow text{A’} (-6,-3)$

$text{B}(2,1) rightarrow text{B’} (-2,-1)$

$text{C}(5,7) rightarrow text{C’} (-5,-7)$

$textbf{(b)}$ $text{B}(2,1) rightarrow text{B’} (8,13)$

$textbf{(c)}$ $text{A}(6,3) rightarrow text{A”’} (3,-6)$

$textbf{(a)}$ Given that Jessica has three fewer candies than twice the number Dante has. If $d$ represents the number of candies Dante has and $j$ represent the number of Jessica’s candies, then equation for this situation can be represented as shown below

$$
j=2d-3
$$

$textbf{(b)}$ Given that Jessica has 19 candies then number of Dante’s candies can be found out by putting the value of $j$ equal to 19 in the equation obtained above

$$
begin{align*}
j&=2d-3\
(19)&=2d-3tag{add 3 to each side}\
19+3&=2d-3+3\
22&=2dtag{divide each side by 2}\
dfrac{22}{2}&=dfrac{2d}{2}\
11&=dtag{interchange sides}\
d&=11
end{align*}
$$

Therefor, Dante has 11 candies.

$textbf{(a)}$ $j=2d-3$

$textbf{(b)}$ 11

a) $2^3=2^x$

Simply, $x=3$

b) $x^3=5^3$

Simply, $x=5$

c) $3^4=3^{2x}$

$4=2x$

$x=4 div 2$

$x=2$

d) $2^7=2^{(2x+1)}$

$7=2x+1$

$7-1=2x$

$6=2x$

$x=3$

$textbf{(a)}$ Derek and Donovan were thinking of making the bases equal on the both side then equating the powers by comparing.

Yes, both the methods will work.

$textbf{(b)}$ Method 1.

$$
begin{align*}
4^4&=16^x \
4^4&=(4^2)^x\
4^4&=4^{2x}\
4&=2x tag{text{by comparing the exponents}}\
x&=2\
end{align*}
$$

Method 2.

$$
begin{align*}
4^4&=16^x \
(2^2)^4&=(2^4)^x\
2^{2cdot 4}&= 2^{4x}\
2^8&= 2^{4x}\
8&=4x tag{text{by comparing the exponents}}\
x&=2
end{align*}
$$

a)

$$
2^{(x+3)}=2^{2x}
$$

$$
x+3=2x
$$

$$
3=2x-x
$$

$$
x=3
$$

b)
$$
3^5=9^{2x}
$$

$$
3^5=(3^2)^{2x}
$$

Using $(a^m)^n=a^{m cdot n}$

$$
3^5=3^{4x}
$$

$$
5=4x
$$

$$
x=dfrac{5}{4}
$$

c)

$$
3^{(2x+1)}=3^3
$$

$$
2x+1=3
$$

$$
2x=3-1
$$

$$
2x=2
$$

$$
x=1
$$

d)
$$
8^{70}=2^x
$$

$$
(2^3)^{70}=2^x
$$

Using $(a^m)^n=a^{m cdot n}$

$$
2^{3 cdot 70}=2^x
$$

$$
2^{210}=2^x
$$

$$
x=210
$$

$$
textbf{(a)}
$$

$$
begin{align*}
11x^2+x^2 &=(4x+8)(3x-3)\
12x^2&=4x(3x-3)+8(3x-3) tag{by Distributive property}\
12x^2&=12x^2 -12x + 24x-24\
12x^2&=12x^2+12x-24tag{subtract $12x^2$ from each side}\
12x^2-12x^2&=12x^2-12x^2+12x-24\
0&=12x-24tag{add 24 to each side}\
0+24&=12x-24+24\
24&=12xtag{divide each side by 12}\
dfrac{24}{12}&=dfrac{12x}{12}\
2&=xtag{interchange sides}\
&boxed{x=2}
end{align*}
$$

$$
textbf{(b)}
$$

$$
begin{align*}
dfrac{x}{3}-dfrac{x}{9}&=6tag{rewrite}\
dfrac{3x}{9}-dfrac{x}{9}&=6tag{multiply each term by 9}\
dfrac{3x}{9}cdot 9-dfrac{x}{9}cdot 9&=6cdot 9\
dfrac{9}{9}cdot 3x-dfrac{9}{9}cdot x&=54\
3x-x&=54\
2x&=54tag{divide each side by 2}\
dfrac{2x}{2}&=dfrac{54}{2}\
&boxed{x=27}
end{align*}
$$

$textbf{(c)}$ For solving this kind of equation, we need to make bases on the both side equal (if we can) so that we can equate the powers.

$$
begin{align*}
6^{x+9}&=36^x\
6^{x+9}&={(6^2)}^xtag{use ${(a^m)}^n=a^{mcdot n}$}\
6^{x+9}&=6^{2x}tag{bases are same, hence power should be equal}\
Rightarrow\
x+9&=2xtag{subtract x from each side}\
x-x+9&=2x-x\
9&=xtag{interchange sides}\
&boxed{x=9}
end{align*}
$$

$textbf{(d)}$
$$
begin{align*}
dfrac{4}{9}+dfrac{1}{a}&=dfrac{2}{3}tag{multiply each side by 9a}\
dfrac{4}{9}cdot 9+dfrac{1}{a}cdot 9 &=dfrac{2}{3}cdot 9\
dfrac{9a}{9}cdot 4+dfrac{9a}{a} &=dfrac{9a}{3}cdot 2\
acdot 4+9&=3acdot 2\
4a+9&=6atag{subtract 4a from each side}\
4a-4a+9&=6a-4a\
9&=2atag{divide each side by 2}\
dfrac{9}{2}&=dfrac{2a}{2}\
4.5&=atag{interchange sides}\
&boxed{a=4.5}
end{align*}
$$

$textbf{(e)}$
$$
begin{align*}
sqrt{x+3}&=6tag{Square each side}\
(sqrt{x+3})^2&=6^2\
x+3&=36tag{subtract 3 from each side}\
x+3-3&=36-3\
&boxed{x=33}
end{align*}
$$

$textbf{(f)}$
$$
begin{align*}
1.2m-0.2&=3.8+mtag{subtract m from each side}\
1.2m-m-0.2&=3.8+m-m\
0.2m-0.2&=3.8tag{add 0.2 to each side}\
0.2m-0.2+0.2&=3.8+0.2\
0.2m&=4tag{divide each side by 0.2}\
dfrac{0.2m}{0.2}&=dfrac{4}{0.2}\
m&=4cdot dfrac{10}{2}\
&boxed{m=20}
end{align*}
$$

$textbf{(g)}$
$$
begin{align*}
(x+12)^2&=9tag{take square root on each side}\
sqrt{(x+12)^2}&=sqrt{9}\
x+12&=pm 3tag{subtract 12 from each side}\
x+12-12&=pm3-12\
x&=-9,-15\
&boxed{x=-9}\
&boxed{x=-15}\
end{align*}
$$

$textbf{(a)}$ 2

$textbf{(b)}$ 27

$textbf{(c)}$ 9

$textbf{(d)}$ 4.5

$textbf{(e)}$ 33

$textbf{(f)}$ 20

$textbf{(g)}$ -9 ; -15

Yes, for part $textbf{(d)}$ and part $textbf{(e)}$ for some input the solutions are not allowed.

$bullet$ In part $textbf{(d)}$ function is not defined for $a=0$ as it will make a term equal to $dfrac{1}{0}$ which is not defined.

$bullet$ In part $textbf{(e)}$ function is not defined for values of x less than -3 as it will result in the negative values inside the square root which will not give values in real numbers and hence these solutions are not allowed.

Yes, for part $textbf{(d)}$ and part $textbf{(e)}$ for some input the solutions are not allowed. For thorough explanation see inside

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
& text{Convert 8x to base 2} \
&left(2^3right)^x=2^6\\
&2^{3x}=2^6 tag{Simplify} \
&3x=6 tag{Simplify} \
&frac{3x}{3}=frac{6}{3} tag{Divide both sides by 3} \
&boxed{color{#c34632}x=2} \
end{align*}
$$

$$
color{#c34632} text{} mathrm{Apply:exponent:rule}:quad left(a^bright)^c=a^{bc}
$$

$$
color{#c34632} text{}mathrm{If:}a^{fleft(xright)}=a^{gleft(xright)}mathrm{,:then:}fleft(xright)=gleft(xright)
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
& text{Convert 9 to base 3} \
&left(3^2right)^2=3^{2x+1}\\
&3^{2cdot :2}=3^{2x+1} tag{Simplify} \
&2cdot :2=2x+1 tag{Simplify} \
&4=2x+1 tag{Simplify}\
&2x+1=4 tag{Switch sides}\
&2x+1-1=4-1 tag{Subtract 1 from both sides}\
&2x=3 tag{Simplify} \
&frac{2x}{2}=frac{3}{2} tag{Divide both sides by 2} \
&boxed{color{#c34632}x=frac{3}{2}} \
end{align*}
$$

$$
color{#c34632} text{} mathrm{Apply:exponent:rule}:quad left(a^bright)^c=a^{bc}
$$

$$
color{#c34632} text{}mathrm{If:}a^{fleft(xright)}=a^{gleft(xright)}mathrm{,:then:}fleft(xright)=gleft(xright)
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
& text{Convert both sides} \
&left(2^2right)^{2x}=left(2^{-1}right)^{x+5}\\
&2^{2cdot :2x}=2^{-1cdot left(x+5right)} \
&2cdot :2x=-1cdot left(x+5right) \
&4x=-left(x+5right) tag{Simplify}\
&4x=-x-5 tag{Expand}\
&4x+x=-x-5+x tag{Add x to both sides}\
&5x=-5 tag{Simplify} \
&frac{5x}{5}=frac{-5}{5} tag{Divide both sides by 5} \
&boxed{color{#c34632}x=-1} \
end{align*}
$$

$$
color{#c34632} text{} mathrm{Apply:exponent:rule}:quad left(a^bright)^c=a^{bc}
$$

$$
color{#c34632} text{}mathrm{If:}a^{fleft(xright)}=a^{gleft(xright)}mathrm{,:then:}fleft(xright)=gleft(xright)
$$

$$
color{#4257b2} text{a)}x=2
$$

$$
color{#4257b2} text{b)}x= frac{3}{2}
$$

$$
color{#4257b2} text{c)}x=-1
$$

Given that every ton of recycled paper saves about 17 trees. which can be also be written as every 2000 pounds of recycled paper saves about 17 trees as there is 2000 pounds in 1 ton.

Every 2000 pounds of recycled paper saves about 17 trees

$Rightarrow$ 1 pound of recycled paper saves number of trees $=dfrac{17}{2000}$

Now, 8000 pound of recycled paper saves number of trees
$$
=dfrac{17}{2000}cdot 8000=17cdot 4=68
$$

Therefore, 8000 pound of recycled paper saves about 68 trees.

$textbf{(a)}$From the attached figure we can see that the base of triangle is of 7 units and perpendicular height is 5 units.
The area of triangle is given by
$$
dfrac{1}{2}times text{base}times text{perpendicular height}
$$

$Rightarrow$
$$
text{Area}=dfrac{1}{2}times 7times 5=17.5 text { unit}^2
$$

$textbf{(b)}$ The resultant figure is shown in the blue colour. The resultant coordinates are as follows

$(-3,3) rightarrow (-6,5)$

$(4,3) rightarrow (1,5)$

$$
(2,-2) rightarrow (-1,0)
$$

$textbf{(a)}$ $17.5 text{unit}^2$

$textbf{(b)}$
$(-3,3) rightarrow (-6,5)$

$(4,3) rightarrow (1,5)$

$$
(2,-2) rightarrow (-1,0)
$$

In the figure above , $measuredangle$ C and 128 $text{textdegree}$ is supplementary pair of angles.

$Rightarrow$
$$
begin{align*}
180text{textdegree} &=measuredangle text{C}+128text{textdegree}\
measuredangle text{C}&= 180text{textdegree} -128 text{textdegree}\
measuredangle text{C}&=52text{textdegree}
end{align*}
$$

$bullet$ $measuredangle text{C}$ and $measuredangle text{d}$ are pairs of equal alternate interior angles.

$Rightarrow$
$$
measuredangle text{c}=measuredangle text{d}=52text{textdegree}
$$

$bullet$ $measuredangle text{x}$ and 72$text{textdegree}$ are again supplementary pairs.
$Rightarrow$ $measuredangle text{x}+72text{textdegree}=180text{textdegree}$

hence
$$
measuredangle text{x}=108text{textdegree}
$$

Now $measuredangle text{x}$ and $measuredangle text{b}$ are the corresponding angles of the given parallel lines, hence they should be equal.
Therefore,
$$
measuredangle text{x}= measuredangle text{b}=108text{textdegree}
$$

$bullet$ $measuredangle text{b}$ and $measuredangle text{a}$ are vertical angles, hence should be equal.

$Rightarrow$
$$
measuredangle text{b} =measuredangle text{a} =108 text{textdegree}
$$

$measuredangle text{a} =108 text{textdegree}$

$measuredangle text{b} =108 text{textdegree}$

$measuredangle text{c} =52 text{textdegree}$

$$
measuredangle text{a} =52 text{textdegree}
$$

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
2left(3x-4right)=22& {;}quad : frac{2left(3x-4right)}{2}=frac{22}{2}tag{Divide both sides by 2}\
&3x-4=11tag{Simplify} \
&3x-4+4=11+4tag{Add 4 to both sides} \
&3x=15tag{Simplify} \
&frac{3x}{3}=frac{15}{3}tag{Divide both sides by 3 } \
&{color{#c34632}x=5}
end{align*}
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
6left(2x-5right)=-left(x+4right)& {;}quad : 12x-30=-x-4tag{Expand}\
&12x-30+30=-x-4+30tag{Add 30 to both sides} \
&12x=-x+26tag{Simplify} \
&12x+x=-x+26+xtag{Add x to both sides } \
&13x=26tag{Simplify} \
&frac{13x}{13}=frac{26}{13}tag{Divide both sides by 13} \
&{color{#c34632}x=2}
end{align*}
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
2-left(y+2right)=3y& {;}quad : 2-y-2=3ytag{Expand}\
&-y=3ytag{Simplify} \
&-y-3y=3y-3ytag{Subtract 3y from both sides} \
&-4y=0tag{Simplify} \
&frac{-4y}{-4}=frac{0}{-4}tag{Divide both sides by -4 } \
&{color{#c34632}y=0}
end{align*}
$$

$$
{color{#4257b2}text{d)}}
$$

$$
begin{align*}
3+4left(x+1right)=159& {;}quad : 3+4left(x+1right)-3=159-3tag{Subtract 3 from both sides}\
&4left(x+1right)=156tag{Simplify} \
&frac{4left(x+1right)}{4}=frac{156}{4}tag{Divide both sides by 4} \
&x+1=39tag{Simplify} \
&x+1-1=39-1tag{Subtract 1 from both sides } \
&{color{#c34632}x=38}
end{align*}
$$

$$
color{#4257b2} text{ a) }x=5
$$

$$
color{#4257b2} text{ b) }x=2
$$

$$
color{#4257b2}text{ c) }y=0
$$

$$
color{#4257b2} text{ d) }x=38
$$