

A novel Goodness of fit test for Multilevel Proportional Odds model Essay Example
Application to a Real-Life Data Set
Throughout this chapter, the purpose was to place how the proposed goodness of fit trial works with the existent life information set. It provides a good apprehension about the fresh trial and can be used to place the belongings of the goodness of fit trial every bit good. Since this trial is developed for multilevel information, an information set that gives a multilevel information construction was selected for this trial-proof procedure. The method of a set using the information set harmonizing to the nature of the trial and besides the application of the fresh goodness of fit trial was clearly discussed through this chapter under the relevant bomber subjects.
Description About the Informations Set
The information set selected for the survey is comparatively big with 31,022 persons in 2280 schools. The information set consisting the consequence of GCSE scrutiny of pupils among 131 instruction governments.
The following table represents the description of the variables which are carried through this illustration.
Table: Description about the var
...iables
| Variable | Description about the variable | Type of the variable |
| ID_LEA | ID for local instruction governments. | ID for the 2nd degree |
| ID_I | ID for persons. | ID for the first degree |
| AGCSE | Average GCSE mark of single centered at mean. | Continuous variable |
| Gender |
Gender of the persons. Male=0 and Female=1 |
Categorical variable ( Male as a basal class ) |
| AGE_MONTHS |
Age in months, centered at 222 months or 18.5 old ages. |
Continuous variable |
Harmonizing to the above tabular array the information set consists of a multilevel nature where it is represented by two degrees. That is as the first degree the ID for persons and as the 2nd degree ID for Local Education Authorities was considered.
Under the survey the involvement was on ordinal categorical response and hence the uninterrupted variable GCSE is categorize
into three classs based on percentiles. The classification is explained under the following subject which is Data readying. Besides the variables GENDER and AGE_MONTHS were selected as the explanatory variables.
Data Preparation
In order to integrate the ordinal categorical informations, the variable GCSE was coded harmonizing to the percentiles values. Three ordered classes of the response were considered to suit the multilevel relative odds theoretical account. Those classes are constructed harmonizing to the undermentioned mode.
Harmonizing to the above the response variable is categorized into three classes based on the percentile values and hence variable is categorized without any biasness and truth of the classification is improved.
Besides, it is of import to observe that this information set consists of 131 bunches and within a bunch, the Numberss of observations are altering. However, the bunch sizes which are well larger are adequate to use the fresh trial and all the 131 bunches are used to suit the theoretical account. The representation of the bunch and bunch sizes can be tabulated as follows.
Table: Description of bunches with regard to their bunch sizes
| Cluster Identity | Cluster size | Cluster Identity | Cluster size | Cluster Identity | Cluster size | Cluster Identity | Cluster size |
| 1 | 41 | 7 | 75 | 13 | 112 | 19 | 220 |
| 2 | 144 | 8 | 10 | 14 | 33 | 20 | 181 |
| 3 | 50 | 9 | 96 | 15 | 357 | 21 | 182 |
| 4 | 22 | 10 | 91 | 16 | 77 | 22 | 67 |
| 5 | 128 | 11 | 35 | 17 | 91 | 23 | 246 |
| 6 | 35 | 12 | 78 | 18 | 224 | ( Continued ) | |
| Cluster Identity | Cluster size | Cluster Identity | Cluster size | Cluster Identity | Cluster size | Cluster Identity | Cluster size |
| 24 | 113 | 54 | 225 | 84 | 314 | 114 | 395 |
| 25 | 155 | 55 | 171 | 85 | 64 | 115 | 510 |
| 26 | 95 | 56 | 65 | 86 | 519 | 116 | 931 |
| 27 | 173 | 57 | 149 | 87 | 65 | 117 | 74 |
| 28 | 111 | 58 | 153 | 88 | 423 | 118 | 969 |
| 29 | 51 | 59 | 289 | 89 | 102 | 119 | 916 |
| 30 | 233 | 60 | 328 | 90 | 190 | 120 | 376 |
| 31 | 151 | 61 | 104 | 91 | 127 | 121 | 408 |
| 32 | 155 | 62 | 333 | 92 | 109 | 122 | 329 |
| 33 | 121 | 63 | 470 | 93 | 217 | 123 | 251 |
| 34 | 703 | 64 | 232 | 94 | 85 | 124 | 661 |
| 35 | 197 | 65 | 69 | 95 | 185 | 125 | 520 |
| 36 | 201 | 66 | 274 | 96 | 150 | 126 | 265 |
| 37 | 57 | 67 | 131 | 97 | 670 | 127 | 321 |
| 38 | 201 | 68 | 55 | 98 | 53 | 128 | 432 |
| 39 | 138 | 69 | 119 | 99 | 96 | 129 | 762 |
| 40 | 149 | 70 | 200 | 100 | 432 | 130 | 391 |
| 41 | 18 | 71 | 235 | 101 | 203 | 131 | 442 |
| 42 | 232 | 72 | 103 | 102 | 75 | ||
| 43 | 147 | 73 | 94 | 103 | 466 | ||
| 44 | 313 | 74 | 28 | 104 | 68 | ||
| 45 | 323 | 75 | 67 | 105 | 278 | ||
| 46 | 256 | 76 | 119 | 106 | 64 | ||
| 47 | 121 | 77 | 115 | 107 | 704 | ||
| 48 | 317 | 78 | 95 | 108 | 469 | ||
| 49 | 160 | 79 | 220 | 109 | 802 | ||
| 50 | 53 | 80 | 71 | 110 | 241 | ||
| 51 | 49 | 81 | 108 | 111 | 364 | ||
| 52 | 207 | 82 | 490 | 112 | 592 | ||
| 53 | 92 | 83 | 152 | 113 | 791 | ||
Above tabular array 5.2 represents the figure of bunches and the sizes of each and every bunch. Altogether there are 31,022 observations among 131 bunches.
Model edifice
In order to suit the theoretical account to the selected information set the MLwiN 2.19 version was used in order to integrate the multilevel nature of the information and to suit the multilevel relative odds theoretical account. The theory behind the theoretical account and the theoretical account edifice procedure was clearly discussed under the Theory and
methodological analysis chapter. In this subdivision the application of those mentioned methods will be discussed. Besides after initializing the theoretical account a relevant parametric quantity appraisal method should be given and consequently 1storder PQL method was used in order to get the better of the convergence jobs that occurred in gauging parametric quantities.
Variable choice
When suiting the theoretical account the variables which significantly make an impact on the response variable should be identified. For this, the forward choice method was used with 5 % degree of significance. In order to take the import variables to the theoretical account the Wald trial statistic was used instead of utilizing the Likelihood ratio trial statistic. The ground behind this is for distinct response multilevel theoretical accounts the likelihood trial is nonavailable in MLwiN. Therefore Wald trial statistic was calculated to prove the significance of the single coefficients in the theoretical account and those values were compared with chi-square one grades of freedom. If the Wald statistic for a covariate is important the peculiar covariate should be included in the theoretical account.
Harmonizing to the above process, by getting downing bit by bit from the smallest theoretical account that is model merely with the changeless term the best theoretical account was selected by adding variables one at a clip. As the first measure, a variable that is traveling to be added to the theoretical account should be selected foremost. For this ab initio, all the variables were added to pattern with changeless terms and among them the most important variable was selected based on the p-values.
Then harmonizing to the p-values the variable which has the lowest p-value was selected as the
variable which should be added foremost to the pattern. The outputs obtained from under this can be tabulated as in the following bomber subject.
Parameter appraisals under forwarding choice process for multilevel relative odds theoretical account
As discussed in the subject above the forward choice method can be carried in the undermentioned mode and the resulted outputs are mentioned consequently.
Each variable was added individually and Wald statistic was calculated for each variable and so the p-value obtained for the trial statistic was compared with 5 % ( 0.05 ) significance degree to look into the significance of variables.
Table: Outputs obtained under phase 1
| Variable | Classs | Estimates-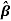 ( venereal disease ( ( venereal disease (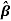 ) ) ) ) |
Wald trial statistic |
P-value |
| Gender |
Female ( Male-Reference ) |
-0.650 ( 0.022 ) | 872.934 | 7.5118e-192* |
| AGE_MONTHS | - | -0.029 ( 0.003 ) | 93.444 | 4.1786e-022* |
significance at 5 %
Harmonizing to the resulted values under phase 1 both the variables are important since the p-values are less than 0.05. Among the two variables GENDER is extremely important when compared with AGE_MONTHS. Therefore GENDER was selected as the first inclusion variable to the theoretical account with the changeless term merely. Harmonizing to the response of involvement which has three classes, the relative odds model gives two logits by sing 3rd class as the base degree. Now the random intercept multilevel relative odds fitted theoretical account after adding GENDER to the changeless merely theoretical account can be written as follows.
Where is the cumulative chance for each class, and stand for the observation index and the bunch ID severally.
As the following measure AGE_MONTHS variable was added to the theoretical account which was fitted under phase 1 and it was checked for significance with the other explanatory variable which is already exists in the theoretical account.
The resulted values under this phase besides tabulated as follows.
Table: Out puts obtained under phase 2
| Variable | Classs | Estimates-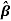 ( venereal disease ( ( venereal disease (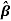 ) ) ) ) |
Wald trial statistic |
P-value |
| AGE_MONTHS | - | -0.029 ( 0.003 ) | 90.150 | 2.2077e-021* |
significance at 5 %
After adding the AGE_MONTHS to the theoretical account with the GENDER variable the covariate AGE_MONTHS is important. Therefore the new theoretical account obtained under phase 2 can be formulated as follows.
0.648 ( 0.022 ) Gender
0.648 ( 0.022 ) Gender
Where is the cumulative chance for each class, and stand for the observation index and the bunch ID severally.
Final chief effects theoretical account
The concluding chief effects model consists of both the covariates that have been selected at the 2nd phase. Therefore the multilevel relative theoretical account fitted by utilizing forward choice process is,
0.648 ( 0.022 ) Gender
0.648 ( 0.022 ) Gender
The is the cumulative chance of the mean GCSE mark of the pupil ( observation unit ) in the local instruction authorization ( bunch ) . Besides harmonizing to the principal of parsimoniousness, the chief effects theoretical account prefer over the interaction theoretical account due to the simpleness and the comprehendible than the interaction theoretical account.
Application of the fresh goodness of fit trial
Under this topic the application of the proposed goodness of fit trial for the multilevel relative odds theoretical account will be discussed. For that, the fitted chief effects theoretical account was applied to the selected information set under subdivision 5.3.
In order to the developed method foremost predicted chances of the fitted theoretical account were calculated and so the predicted mean tons were calculated. The computation of the predicted mean tons is mentioned under the theory and methodological analysis chapter. Now based on the
predicted mean tons observations of each bunch should be partitioned. The figure of divider used here is 10 and it is non a fixed value. But harmonizing to Hosmer and Lemeshow ( 1980 ), 10 is the most celebrated value for the figure of groups. Then the 10 groups are such that the first group contains the smallest values of the predicted mean tons and the ten percent group contains the largest values of the predicted mean tons.
By partitioning the information, the goodness of tantrum of the trial is conducted by making nine index variables for each bunch. 1if is in part g = 0 otherwise where is the predicted mean mark for the pupil in the bunch and .
Then to measure the theoretical account adequateness of the fitted theoretical account in equation 5.1, an alternate theoretical account is constructed by adding 10 index variables and theoretical account contains 9 index variables since first index variable was selected to be the basal class.
Harmonizing to the information set of the selected illustration most of the Numberss of observations within bunches are non-divisible by 10 in order to make index variables. To get the better of this job the method discussed by Abeysekara and Sooriyarachchi (2008) , was used where index variables can be defined as follows.
Here and is the index variable.
As the aim, it is interested to look into the adequateness of the fitted theoretical account the nothing and the alternate hypothesizes can be stated as, Hydrogen O: fitted multilevel relative odds theoretical account is equal. Hydrogen1: Fitted multilevel relative odds theoretical account is non-equal
Harmonizing to the above hypothesis so to measure the theoretical account adequateness
of the fitted chief effects model, the alternate theoretical account is constructed by adding index variables as follows. Where is the index variable for the group for observation in the bunch. If the fitted theoretical account is equal so, the Hydrogen O: Fitted multilevel relative odds theoretical account is equal to the information is non rejected and it implies that the coefficients of all index variables.
Harmonizing to the above, discussed hypothesis is tested by utilizing MLwiN package. Consequently, the joint Wald trial statistic of the alternate theoretical account was calculated in order to look into the undermentioned hypothesis. That is all the coefficients of index variables are equal to zero. At least the coefficient of the index variable is non-equal to zero. The end product of the resulted articulation Wald trial statistic can be tabulated as follows.
Table: The end product of joint Wald trial statistic
|
Joint Wald trial Statistic |
Degrees of freedom |
Chi-square value ( Tabulated at 5 % ) |
p-value |
| 11.365 | 9 | 16.9 | 0.25152 |
Harmonizing to the end product values of the above tabular array 5.5, the p-value of the joint Wald trial statistic is greater than 0.05 ( 5 % degree significance ) proposing non rejecting the void hypothesis that is at 5 % degree of significance. On the other manus this is clearly shown by the Wald trial statistic value every bit good. Because it is less than the chi-square value, with 5 % degree of significance and 9 grades of freedom ( 11.365 & A; lt; 16.9 ). This consequence concludes that the alternate theoretical account that is model with index variables is non-equal to the information. It gives the fitted chief effects model under 5.1 is well fitted to the information.
Finally
all the above suggest the fresh goodness of fit trial fitted for multilevel relative odds theoretical account is equal to the selected illustration information set.
Outline
Throughout this chapter the application of the proposed goodness of fit trial to the multilevel relative odds theoretical account was discussed. There a multilevel relative odds theoretical account was fitted to an existent life information set and so the fresh trial was applied in order to measure the adequateness of the fitted theoretical account. Harmonizing to the consequences obtained through this application, it was suggested that the fresh goodness of fit trial works with the existent life information every bit good.
The following chapter will transport out the general treatment of all the findings and the decisions obtained throughout this research survey. Finally, it presents the restrictions and suggestions for further surveys.
- Nineteen Eighty-Four essays
- Maus essays
- Research Methods essays
- Experiment essays
- Hypothesis essays
- Observation essays
- Qualitative Research essays
- Theory essays
- Explorer essays
- Normal Distribution essays
- Probability Theory essays
- Variance essays
- Agriculture essays
- Albert einstein essays
- Animals essays
- Archaeology essays
- Bear essays
- Biology essays
- Birds essays
- Butterfly essays
- Cat essays
- Charles Darwin essays
- Chemistry essays
- Dinosaur essays
- Discovery essays
- Dolphin essays
- Elephant essays
- Eli Whitney essays
- Environmental Science essays
- Evolution essays
- Fish essays
- Genetics essays
- Horse essays
- Human Evolution essays
- Isaac Newton essays
- Journal essays
- Linguistics essays
- Lion essays
- Logic essays
- Mars essays
- Methodology essays
- Mineralogy essays
- Monkey essays
- Moon essays
- Mythology essays
- Noam Chomsky essays
- Physics essays
- Plate Tectonics essays
- Progress essays
- Reaction Rate essays



