Please enter something
Home Page Sports Baseball Analysis of the Salaries of 100 Baseball Players Essay Example
Analysis of the Salaries of 100 Baseball Players Essay Example
Analysis of the Salaries of 100 Baseball Players Essay Example

Analysis of the Salaries of 100 Baseball Players Essay Example

Available Only on StudyHippo
Topics:
Baseball, Mathematics, Mean, Variance
View Entire Sample
Text preview

Undertaking 1

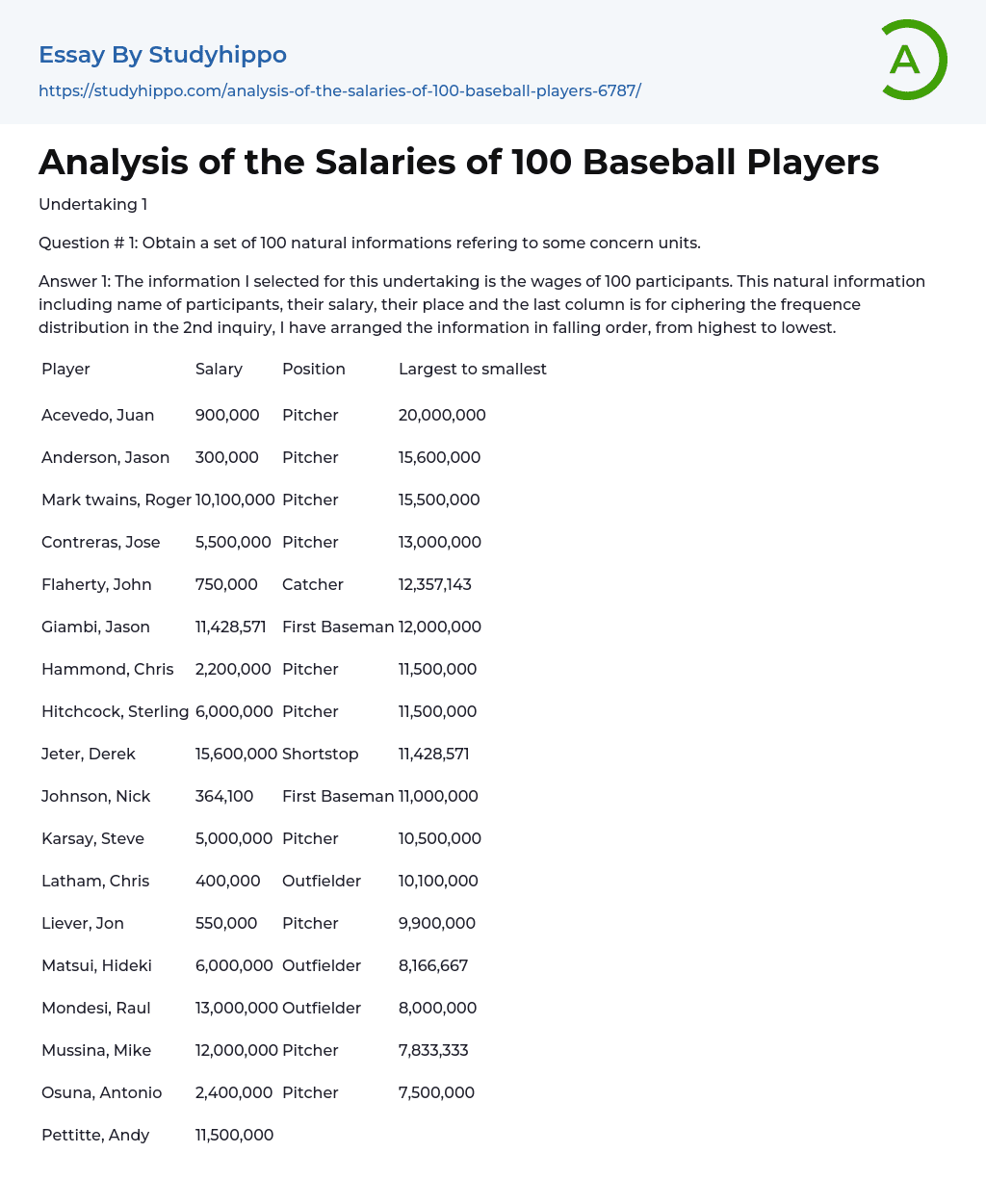
Question # 1: Obtain a set of 100 natural informations refering to some concern units.

Answer 1: The information I selected for this undertaking is the wages of 100 participants. This natural information including name of participants, their salary, their place and the last column is for ciphering the frequence distribution in the 2nd inquiry, I have arranged the information in falling order, from highest to lowest.

Player Salary Position Largest to smallest
Acevedo, Juan 900,000 Pitcher 20,000,000
Anderson, Jason 300,000 Pitcher 15,600,000
Mark twains, Roger 10,100,000 Pitcher 15,500,000
Contreras, Jose 5,500,000 Pitcher 13,000,000
Flaherty, John 750,000 Catcher 12,357,143
Giambi, Jason 11,428,571 First Baseman 12,000,000
Hammond, Chris 2,200,000 Pitcher 11,500,000
Hitchcock, Sterling 6,000,000 Pitcher 11,500,000
Jeter, Derek 15,600,000 Shortstop 11,428,571
Johnson, Nick 364,100 First Baseman 11,000,000
Karsay, Steve 5,000,000 Pitcher 10,500,000
Latham, Chris 400,000 Outfielder 10,100,000
Liever, Jon 550,000 Pitcher 9,900,000
Matsui, Hideki 6,000,000 Outfielder 8,166,667
Mondesi, Raul 13,000,000 Outfielder 8,000,000
Mussina, Mike 12,000,000 Pitcher 7,833,333
Osuna, Antonio 2,400,000 Pitcher 7,500,000
Pettitte, Andy 11,500,000 Pitcher 7,250,000
Posada, Jorge 8,000,000 Catcher 7,250,000
Rivera, Mariano 10,500,000 Pitcher 7,166,667
Soriano, Alfonso 800,000 Second Baseman 6,750,000
Trammell, Bubba 2,500,000 Outfielder 6,750,000
Ventura, Robin 5,000,000 Third Baseman 6,000,000
Weaver, Jeff 4,150,000 Pitcher 6,000,000
Wells, David 3,250,000 Pitcher 5,500,000
Williams, Bernie 12,357,143 Outfielder 5,500,000
Wilson, Enrique 700,000 Shortstop 5,350,000
 

Zeile, Todd
1,500,000 Third Baseman 5,125,000
Anderson, Garret 5,350,000 Outfielder 5,000,000
Appier, Kevin 11,500,000 Pitcher 5,000,000
Callaway, Mickey 302,500 Pitcher 4,700,000
Donnelly, Brendan 325,000 Pitcher 4,250,000
Eckstein, David 425,000 Shortstop 4,150,000
Erstad, Darin 7,250,000 Outfielder 4,000,000
Fullmer, Brad 1,000,000 First Baseman 4,000,000
Gil, Benji 725,000 Shortstop 3,916,667
Glaus, Troy 7,250,000 Third Baseman 3,875,000
Kennedy, Adam 2,270,000 Second Baseman 3,625,000
Lackey, John 315,000 Pitcher 3,450,000
Molina, Benjie 1,425,000 Catcher 3,250,000
Molina, Jose 320,000 Catcher 3,000,000
Ortiz, Ramon 2,266,667 Pitcher 2,900,000
Owens, Eric 925,000 Outfielder 2,500,000
Percival, Troy 7,833,333 Pitcher 2,400,000
Ramirez, Julio 300,000 Outfielder 2,270,000
Rodriquez, Francisco 312,500 Pitcher 2,266,667
Salmon, Tim 9,900,000 Outfielder 2,200,000
Schoeneweis, Scott 1,425,000 Pitcher 2,100,000
Sele, Aaron 8,166,667 Pitcher 2,000,000
Shields, Scot 305,000

>Pitcher

2,000,000
Spiezio, Scott 4,250,000 First Baseman 1,850,000
Washburn, Jarrod 3,875,000 Pitcher 1,700,000
Weber, Ben 375,000 Pitcher 1,500,000
Wise, Matt 302,500 Pitcher 1,500,000
Wooten, Shawn 337,500 Catcher 1,425,000
Burkett, John 5,500,000 Pitcher 1,425,000
Damon, Johnny 7,500,000 Outfielder 1,250,000
Embree, Alan 3,000,000 Pitcher 1,000,000
Fossum, Casey 324,500 Pitcher 1,000,000
Fox, Chad 500,000 Pitcher 925,000
Garciaparra, Nomar 11,000,000 Shortstop 900,000
Giambi, Jeremy 2,000,000 Outfielder 900,000
Gonzalez, Dicky 300,000 Pitcher 805,000
Hillenbrand, Shea 407,500 Third Baseman 800,000
Howry, Bobby 1,700,000 Pitcher 750,000
Jackson, Damian 625,000 Shortstop 725,000
Lowe, Derek 3,625,000 Pitcher 700,000
Lyon, Brandon 309,500 Pitcher 625,000
Martinez, Pedro 15,500,000 Pitcher 550,000
Mendoza, Ramiro 2,900,000 Pitcher 500,000
Millar, Kevin 2,000,000 First Baseman 500,000
Mirabelli, Doug 805,000 Catcher 425,000
Mueller, Bill 2,100,000 Third Baseman 407,500
Nixon, Trot 4,000,000 Outfielder 400,000
Ortiz, David 1,250,000 First Baseman 400,000
Person, Robert 300,000 Pitcher 375,000
Ramirez, Manny 20,000,000 Outfielder 364,100
Timlin, Mike 1,850,000 Pitcher 337,500
Varitek, Jason 4,700,000 Catcher 330,000
Wakefield, Tim 4,000,000 Pitcher 325,000
Walker, Todd 3,450,000 Second Baseman 324,500
White, Matt 300,000 Pitcher 320,000
Anderson, Brian
1,500,000 Pitcher 315,000 Baez, Danys 5,125,000 Pitcher 314,400 Bard, Josh 302,100 Catcher 314,300 Bere, Jason 1,000,000 Pitcher 312,500 Blake, Casey 330,000 Third Baseman 309,500 Bradley, Milton 314,300 Outfielder 307,500 Broussard, Benjamin 303,000 First Baseman 305,000 Martha jane burks, Ellis 7,166,667 Outfielder 303,000 Davis, Jason 301,100 Pitcher 302,500 Garcia, Karim 900,000 Outfielder 302,500 Gutierrez, Ricky 3,916,667 Shortstop 302,200 Hafner, Travis 302,200 First Baseman 302,100 Laker, Tim 400,000 Catcher 301,100 Lawton, Matt 6,750,000 Outfielder 300,900 Cleveland Indians 6,750,000 Outfielder 300,900 Cleveland Indians 300,900 Pitcher 300,000 Cleveland Indians 314,400 Shortstop 300,000 Cleveland Indians 500,000 Pitcher 300,000 Cleveland Indians 307,500 Pitcher 300,000 Cleveland Indians 300,900 Shortstop 300,000

Question # 2: Concept a frequence distribution and histogram for the informations utilizing 7 or 8 categories.

Answer 2: Frequency Distribution: the distribution of frequence in a interval is the figure of observations. The interval size used depends on the information. If the information is big so the interval is big and if the information is little so the interval is little. An of import point that must be kept in head while doing intervals is that they must non overlap one another and it mus

View entire sample
Join StudyHippo to see entire essay

incorporate all the possible observation nowadays.

For the intent of happening frequence distribution, I found out lowest wage and highest wage from the sample, which is as follows:

Lowest salary = 300,000 and highest salary = 20,000,000

This lower and highest wage can besides be referred as lower category boundary which is little figure that can be represented in different categories, whereas, upper category boundary is the highest figure that can belong to the different categories.

I had an option of choosing either 7 or 8 categories so:

Number of categories = 8

The Range of my informations = 20,000,000 – 300,000 = 19,700,000

Class breadth which is besides known as the size of interval =

For ciphering the category bounds, I have added 2,462,500 in 300,000 which is the lowest wage to acquire 2,762,500. For the 2nd bound I have once more repeated this process and added 2,462,500 to acquire 5,225,001. I have repeated this for all category limits computation. To avoid informations from over lapping I have increased 1 figure at the terminal of each category bound.

Class bounds Frequency Upper bound
300,000 - 2,762,500 5 300,000
2,762,501 - 5,225,001 55 2762501
5,225,002 - 7,687,502 15 5,225,002
7,687,503 - 10,150,003 11 7,687,503
10,150,004 - 12,612,503 5 10,150,004
12,612,504 - 15,075,004 7 12,612,504
15,075,005 - 17,537,505 1 15,075,005
17,537,506 - 20,000,005 2 17,537,506

Histogram:

It is fundamentally a graph that shows the information with the aid of bars of assorted highs. In a histogram Numberss are grouped in intervals and frequences. The tallness of a peculiar saloon depends on scope of interval. It varies from one scope to another. For doing histogram, I used informations analysis in excel. Bin is the upper category bound that I calculated for the intent of doing category bounds. For doing histogram, bin and frequence are required ; I used them both as shown:

Bin Frequency
300,000 5
2,762,501 55
5,225,002 15
7,687,503 11
10,150,004 5
12,612,504 7
15,075,005 1
17,537,506 2
More 1

The histogram formed

from this tabular array is:

Question # 3: What can you detect from the histogram about informations?

Answer 3: In the histogram shown above, Frequency is plotted at the perpendicular axis ( y-axis ) and Bin is plotted at the horizontal axis ( x-axis ) . To understand and construe a histogram, it’s of import to understand frequence foremost. Frequency is the figure of times a peculiar character or figure is found in a given sample.

In my sample, I have calculated the frequence of the figure of times a peculiar sum of wage is found in the sample. For illustration, the wage of 300,000 if found 5 times in the sample and so hold the frequence of 5.

This histogram tells that the wage of $ 2,762,501 has the highest frequence of 55 which means that this is the salary most common amongst the participants. Similarly, the lowest frequence in our sample is 1 with the sum of salary $ 15,075,005 which is the most uncommon amongst participants.

Other observations of histogram are as follows, the wage of 300,000 has a frequence of 5 which means that there are 5 participants who have the wage of 300,000. Another observation shows that 15 participants have the wage of 5,225,002, 11 participants have the wage of 7,687,503, 5 participants have the wage of 10,150,004 and 7 participants have the wage of 12,612,504.

Question # 4: Find mean, average and manner.

Answer # 4: mean is the mean figure, it represents a sample and if in a sample norm is used for computations, consequences will be the same if original values are used, whereas, median is the in-between figure in a set of informations.

And manner is the figure that occurs most often in a set of informations.

I calculated the mean, average and manner for the informations utilizing excel and computation is shown in the affiliated excel file above is:

Mean 3,615,811
Median 1,775,000
Manner 300000

The norm of our sample is 3,615,811 which represents our set of informations, median is 1,775,000 which is the center or in-between figure of our sample and manner is 3000,000 which is the most perennial figure of our sample.

Question # 5: Find the sample standard divergence and discrepancy.

Answer # 5: standard divergence of a sample measures that in a peculiar distribution, how much are Numberss spread out, it shows that in a peculiar sample, how much divergence is at that place between the value and mean of the sample. A simple expression for mean is variance’s square root. Variance besides measures the discrepancy of values from the mean.

Both standard divergence and discrepancy are used for ciphering discrepancy in the information. Both measures the scattering of informations and are really of import steps of statistics. The computation for mensurating discrepancy is non every bit simple as that of standard divergence.

Similarly, I calculated the standard divergence and fluctuation utilizing excel:

Standard divergence 4240353.494
Variation 1.79806E+13

This standard divergence shows that our sample have divergence of 4240353 from the mean and fluctuation of 1.798.

Question # 6: Compare mean and average and province which you prefer as a step of location of these informations and why?

Answer # 6: Average calculates the mean value for a given sample which means that it calculates the in-between figure in a sample. The value that we obtain after ciphering average fundamentally represents the whole sample and can replace all Numberss in the sample

and still give the same consequence. So the mean here shows the mean sum of salary given to participants i.e. 3,615,811.

On the other manus, median is the in-between figure in a sample. Although mean and average sounds same but there is a batch of difference which I will discourse subsequently. The median for my sample is $ 1,775,000.

I prefer average as a step of location for this information because with mean there is a job of outlier. For illustration, suppose we have to happen average and average of 1,2,3,4 and 100. Mean for this sample is 22 which can non stand for this sample whereas median is 3 which is more accurate. Mean is so high merely because of the outlier 100 and average is unaffected by this and merely finds the in-between figure.

Question # 7: What is the co efficient of fluctuation for this sample?

Answer # 7: Co-effeicient of fluctuation is besides used for mensurating scattering in the information of a distribution of frequence. It is calculated by the formula Standard Deviation / Mean. Sometimes the value of the coefficient of fluctuation is known as the standard relation divergence which is in per centum. For computation of coefficient of fluctuation, a graduated table of ratio must be used as such a graduated table measures merely positive value which is the demand for such steps. An illustration of ratio graduated table is the graduated table of Kelvin which have a void value that is absolute and can non take negative values compared to other graduated tables for mensurating temperatures that can accept both positive and negative values.

Coefficient of fluctuation have different significance in the universe

of stats and different in the universe of puting where it is used to mensurate the sum if hazard inherent in an investing. If coefficient of fluctuation is low than it means that the hazard from the investing is low and of its high, it means that the hazard from puting is high. Not merely coefficient of fluctuation, mean and standard divergence are besides interpreted on the footing of hazard in investings.

It is utile to cipher this step because this does non depend on the unit in which we take measurement. This helps in comparing informations irrespective of the unit of informations which makes comparing really easy. So for the intent of comparing of informations, coefficient of fluctuation must be used alternatively of standard divergence.

One drawback of coefficient of fluctuation is that it is really sensitive to the alterations in mean. This frequently happens for values that are non measured utilizing the graduated table of ratio.

The coefficient of fluctuation is besides calculated utilizing excel, which is 1.172. This shows that this is the sum of fluctuation in our informations.

coefficient of fluctuation 1.172725448

Question # 8: What is the Z mark for your informations that has maximum/minimum value?

Answer # 8: a z-score measures the relation of a mark to the mean of given sample of informations. If the value of z-score is 0 so it means that the mean and mark are equal. It can besides be negative or positive which shows that how much difference above or below is at that place from the standard divergence. It is besides known as the mark that is standard.

This mark is really of import in stats as it measures the

chance that how much a mark occurs and it besides enables comparing of two tonss. In order to happen the z-score, foremost we need to happen the standard divergence of informations and the mean of the information. The difference of mean and value is divided by the divergence to happen the z-score.

The z-score that I found for my informations are as follows:

Largest to smallest z-score
20,000,000 4
15,600,000 3
15,500,000 3
13,000,000 2
12,357,143 2
12,000,000 2
11,500,000 2
11,500,000 2
11,428,571 2
11,000,000 2
10,500,000 2
10,100,000 2
9,900,000 1
8,166,667 1
8,000,000 1
7,833,333 1
7,500,000 1
7,250,000 1
7,250,000 1
7,166,667 1
6,750,000 1
6,750,000 1
6,000,000 1
6,000,000 1
5,500,000 0
5,500,000 0
5,350,000 0
5,125,000 0
5,000,000 0
5,000,000 0
4,700,000 0
4,250,000 0
4,150,000 0
4,000,000 0
4,000,000 0
3,916,667 0
3,875,000 0
3,625,000 0
3,450,000 0
3,250,000 0
3,000,000 0
2,900,000 0
2,500,000 0
2,400,000 0
2,270,000 0
2,266,667 0
2,200,000 0
2,100,000 0
2,000,000 0
2,000,000 0
1,850,000 0
1,700,000 0
1,500,000 0
1,500,000 0
1,425,000 -1
1,425,000 -1
1,250,000 -1
1,000,000 -1
1,000,000 -1
925,000 -1
900,000 -1
900,000 -1
805,000 -1
800,000 -1
750,000 -1
725,000 -1
700,000 -1
625,000 -1
550,000 -1
500,000 -1
500,000 -1
425,000 -1
407,500 -1
400,000 -1
400,000 -1
375,000 -1
364,100 -1
337,500 -1
330,000 -1
325,000 -1
324,500 -1
320,000 -1
315,000 -1
314,400 -1
314,300 -1
312,500 -1
309,500 -1
307,500 -1
305,000 -1
303,000 -1
302,500 -1
302,500 -1
302,200 -1
302,100 -1
301,100 -1
300,900 -1
300,900 -1
300,000 -1
300,000 -1
300,000 -1
300,000 -1
300,000 -1

Question # 9: Draw an Ogive for this distribution and happen average utilizing this.

Answer # 9: the cumulative frequence is defined as the amount of frequences. it is used for the analysis of informations and the cumulative frequence value shows the sum or figure of informations or features below the current value.

For happening the cumulative frequence at a given point, we add old value of cumulative frequence to the present value of frequence. First value in the information set has same frequence and cumulative frequence. For our sample, I have calculated the cumulative frequence utilizing excel which is:

Frequency Accumulative Frequency Accumulative Frequency %
5 5 0.04950495
55 60 0.594059406
15 75 0.742574257
11 86 0.851485149
5 91 0.900990099
7 98 0.97029703
1 99 0.98019802
2 101 1

Graph of cumulative frequence is known as Ogive. This curve shows the cumulative frequence for a given information set. In this graph, we plot cumu

Related assignments
Popular Essay Topics
Get an explanation on any task
Get unstuck with the help of our AI assistant in seconds
New
Get unstuck with AI assistant right now
  • Enter your topic/question
  • Receive an explanation
Pro tips to get quality response
  • Ask one question at a time
  • Enter a specific assignment topic
  • Aim at least 500 characters
Question
What is the right structure for an essay
Answer
A paragraph is a related group of sentences that develops one main idea. Each paragraph in the body of the essay should contain:
  • a topic sentence that states the main or controlling idea
  • supporting sentences to explain and develop the point you’re making
  • evidence from your reading or an example from the subject area that supports your point
  • analysis of the implication/significance/impact of the evidence finished off with a critical conclusion you have drawn from the evidence.