Atomic Structure & Chemistry – Flashcards
Unlock all answers in this set
Unlock answersquestion
periodic table
answer
A table that shows the elements, their atomic number, symbol, and average atomic mass; elements with similar chemical properties are grouped together.
question
Dmitri Mendeleev

answer
created 1st periodic table
question
element
answer
A pure substance made of only one kind of atom; every element on the chart has a neutral charge. cannot be broken down chemically
question
family/group

answer
elements in the same vertical column of the periodic table
question
metals
answer
good conductors of heat and electricity; shiny; ductile; malleable
question
alkali metals
answer
Group 1, 1 electron in outer level, most reactive, soft, silver, shiny, low density; Lithium, Sodium, Potassium, Rubidium, Cesium, Francium
question
alkaline earth

answer
Group 2 of the periodic table: metallic elements which are harder than the alkali metals and are also less reactive
question
transition metals
answer
Groups 3-12, 1-2 electrons in the outer energy level, less reactive than alsali-earth metals, shiny, good conductor of thermal energy and electrical current, high density
question
metalloid
answer
have properties of both metals and nonmetals; solids; dull; ductile; malleable
question
nonmetal

answer
Group of elements that may be solids, liquids, or gases at room temp and tend to be poor conductors of heat and electricity, and NOT malleable, ductile, or lustrous
question
boron family

answer
3 valence electrons, hard and brittle, never found free in nature; Group 13
question
carbon family

answer
Group 14. 4 valence electrons. Includes non-matels, metalloids, and metals.
question
nitrogen family
answer
Group 15. 5 valence electrons. Also includes non-matels, metalloids, and metals.
question
oxygen family

answer
Group 16. The oxygen family is split between nonmetals and metalloids. Each has 6 valence electrons. Very reactive; can combine with most all elements.
question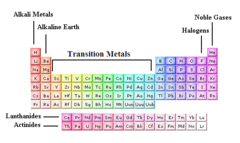
noble gases

answer
Elements in group 18 of the periodic table. Have no charge and are gases under normal conditions. (Helium, Neon, Argon, Krypton, Xenon, Radon). colorless; inert; extremely non-reactive - have full electron shells.
question
halogens
answer
Group 17. Contain nonmetals, 7 valence electrons in it's outermost energy level. Very reactive. ''salt formers"
question
lanthanides
answer
14 elements with atomic number 58-71 (shiny metals similar in reactivity to to alkaline earth metals); synthetic (man-made)
question
actinides

answer
14 elements with the atomic numbers from 90-103. Most of these are man made and some are radioactive. (f-block)
question
period
answer
A horizontal row of elements in the periodic table; the period number equals the number of energy levels.
question
symbol
answer
always uppercase for first letter; second letter is always lowercase
question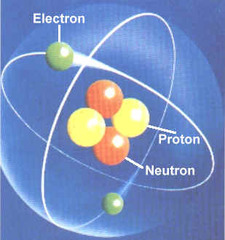
atom

answer
Smallest particle of an element; made up of subatomic particles: protons, neutrons, and electrons.
question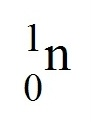
neutron
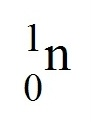
answer
A neutral subatomic particle that is found in the nucleus of an atom
question
proton
answer
A subatomic particle that has a positive charge and that is found in the nucleus of an atom
question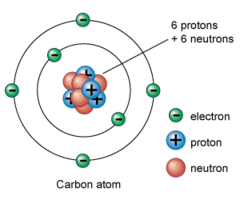
electron

answer
A negatively charged particle that is found outside the nucleus of an atom.
question
atomic number

answer
Number of protons in the nucleus (atomic number = protons).
question
atomic mass
answer
equals protons + neutrons
question
molecule

answer
(physics and chemistry) the simplest structural unit of an element or compound
question
bohr model
answer
A diagram of an atom: neutrons and protons in the nucleus and electrons orbiting around the nucleus.
question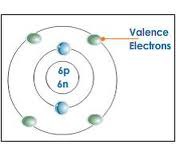
valence electrons

answer
in the outer energy level of an atom; transferred/shared when atoms bond together
question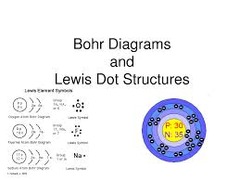
Lewis Dot Structure

answer
The symbol of an element surrounded by an number of dots equal to the number of electrons in the valence shell of the atom.
question
compound
answer
A substance made up of atoms of two or more different elements joined by chemical bonds
question
ion
answer
An atom or group of atoms that has a positive or negative charge.
question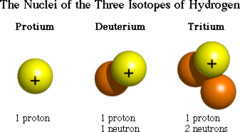
isotope

answer
Atoms of the same element that have different numbers of neutrons
question
solids
answer
A state of matter in which the object has a definite shape and volume.
question
chemical reaction
answer
A process during which chemical bonds between atoms are broken and new ones are formed. Producing one or more different substances.
question
product
answer
A chemical substance formed as a result of a chemical reaction
question
reactants
answer
Elements or compounds that enter into a chemical reaction.
question
chemically stable
answer
describes an atom whose outer energy level is completely filled with all the electrons allowed in that level
question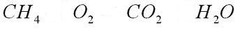
chemical formula
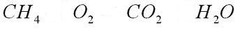
answer
A combination of chemical symbols and numbers to represent a substance.



