Mean, Median, Correlation, Standard Deviation, Five Number Summary and others. – Flashcards
Unlock all answers in this set
Unlock answersquestion
Mean

answer
The mean is the average of the numbers. (In other words it is the sum divided by the count)
question
Median

answer
The Median is the "middle" of a sorted list of numbers. (To find the Median, place the numbers in value order and find the middle.)
question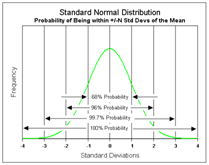
Standard Deviation

answer
Standard deviation is a measure of the dispersion of a set of data from its mean. The more spread apart the data, the higher the deviation. Standard deviation is calculated as the square root of variance.
question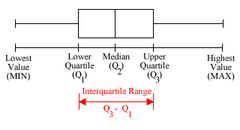
Five Number Summary

answer
For a set of data, the minimum, first quartile, median, third quartile, and maximum. (A boxplot is a visual display of the five-number summary.)
question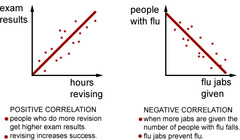
Correlation

answer
A link between two variables is called a correlation. == Associations between variables, and if an association or a relationship exists between two variables, it means that the average value of one variable changes as the value of the other variable is changed.
question
Simpson' Paradox

answer
Simpson's Paradox is a statistical phenomenon where the data seems to prove the reverse of the truth === (Simpson's Paradox is caused by a combination of a lurking variable and data from unequal sized groups being combined into a single data set. The unequal group sizes, in the presence of a lurking variable, can weight the results incorrectly. This can lead to seriously flawed conclusions. The obvious way to prevent it is to not combine data sets of different sizes from a diverse sources.)
question![Causation [ or causality] Causation [ or causality]](https://studyhippo.com/wp-content/uploads/2018/05/causation-or-causality.png)
Causation [ or causality]
![Causation [ or causality] Causation [ or causality]](https://studyhippo.com/wp-content/uploads/2018/05/causation-or-causality.png)
answer
Causation, or causality, is the capacity of one variable to influence another. == The capacity of one variable to influence another. The first variable may bring the second into existence or may cause the incidence of the second variable to fluctuate. === (Note: Causation is often confused with correlation, which indicates the extent to which two variables tend to increase or decrease in parallel. However, correlation by itself does not imply causation.)



